9.10: Electronic Spectra of Organic Molecules
- Page ID
- 22227
General Characteristics
A year after Herschel discovered infrared radiation, Johann Ritter discovered radiation beyond the violet end of the visible spectrum. This radiation came to be known as ultraviolet and soon was recognized as being especially effective in causing chemical reactions. Absorption of light in the ultraviolet and visible regions produces changes in the electronic energies of molecules associated with excitation of an electron from a stable to an unstable orbital. Because the energy required to excite the valence-shell electrons of molecules is comparable to the strengths of chemical bonds, absorption may lead to chemical reactions. We discussed this briefly in Chapter 4 in connection with photochemical halogenation of alkanes; a more detailed account of photochemistry is given in Chapter 28.
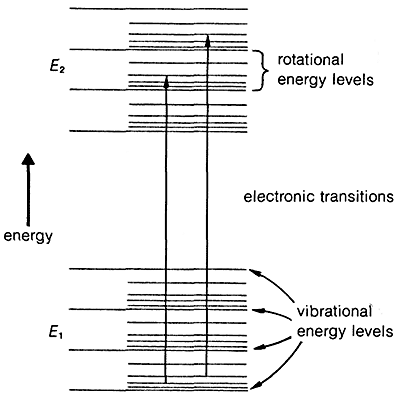
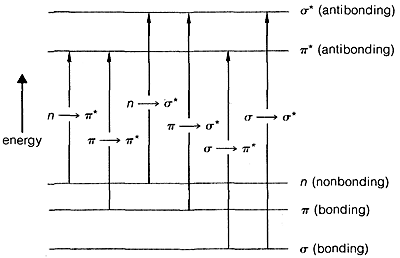
The transition of an electron from the ground state, \(E_1\), to an excited electronic state, \(E_2\), is accompanied by vibrational and rotational changes in the molecule, as shown in Figure 9-17. In condense phase samples, it usually is not possible to resolve the resulting absorption bands well enough to see the fine structure due to vibration-rotation transitions. Consequently, absorptions due to electronic excitation are relatively broad.
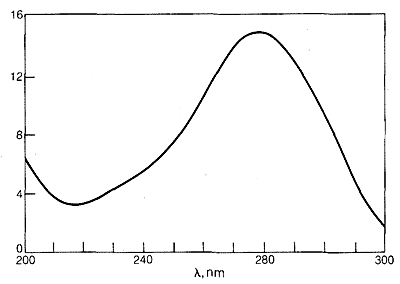
The ultraviolet spectrum of 2-propanone (acetone) is shown in Figure 9-18. The weak absorption, which peaks (i.e., has \(\lambda_\text{max}\) at \(280 \: \text{nm}\), is the result of excitation of one of the unshared electrons on oxygen to a higher energy level. This is called an \(n \rightarrow \pi^*\) (often \(N \rightarrow A\)) transition, in which \(n\) denotes that the excited electron is one of the unshared \(n\) electrons on oxygen and \(\pi^*\) (pi star) denotes that the excited electron goes to a high-energy antibonding orbital of the carbon-oxygen double bond (cf. Sections 6-2 and 6-4C). The same kind of \(n \rightarrow \pi^*\) transition occurs at about the same wavelength and intensity for many simple compounds of the type \(\ce{R_2C=O}\) and \(\ce{RCH=O}\), in which \(R\) is an alkyl group. In a very schematic way, we can write
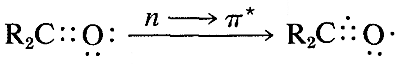
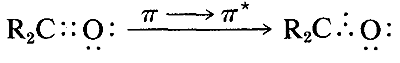

Effects of Conjugation on Electronic Spectra
The \(\pi \rightarrow \pi^*\) transition for ethene has \(\lambda_\text{max} = 175 \: \text{nm}\) and \(\epsilon_\text{max} = 10,000\). It would be expected that an alkadiene would give an absorption spectrum similar to that of ethene but with a larger \(\epsilon\), because there are more double bonds per mole to absorb radiation. This expectation is more or less realized for compounds such as 1,5-hexadiene and 1,3-dimethylenecyclobutane, which have isolated double bonds, but not for 1,3-butadiene or ethenylbenzene, which have conjugated double bonds (Section 3-3):


In general, conjugated systems of double bonds absorb radiation of longer wavelengths and with greater intensity than corresponding systems of isolated double bonds. This means that the difference in energy between the normal and excited states of conjugated systems is less than for isolated systems of double bonds. For 1,3-butadiene and 1,5-hexadiene we can calculate from Equation 9-2
that the transition energy is about \(23 \: \text{kcal}\) less for the conjugated system. The ground state of 1,3-butadiene is stabilized by perhaps \(3 \: \text{kcal}\) relative to a nonconjugated system of double bonds, which means that the excited state must be much more stabilized than this if the transition energy is to be \(23 \: \text{kcal}\) less than for 1,5-hexadiene.
Why is the excited state of a conjugated system of double bonds stabilized more, relative to the ground state, than for a nonconjugated system? Resonance theory provides an explanation (see Section 6-5). Of the several conventional valence-bond structures that can be written for 1,3-butadiene, four of which are shown here, \(2a\)-\(2d\), only structure \(2a\) has a low enough energy to be dominant for the ground state of 1,3-butadiene:
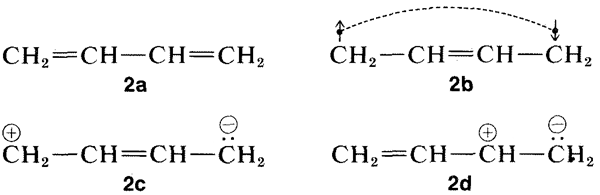
Now, when the molecule is excited to the extent of \(132 \: \text{kcal mol}^{-1}\) by \(217 \: \text{nm}\) ultraviolet light, its energy is so large that pairing schemes such as \(2b\), \(2c\), and \(2d\), which are too unfavorable to contribute very much to the ground state, can be very important for the excited state. Thus the stabilization energy of the excited state, which has a multiplicity of nearly equal-energy pairing schemes, is expected to be greater than that of the ground state with one dominant pairing scheme.
The more double bonds in the conjugated system, the smaller the energy difference between the normal and excited states. The diphenylpolyenes of formula \(C_6H_5-(CH=CH)_n-C_6H_5\) absorb radiation at progressively longer wavelengths as \(n\) is increased. This is apparent from the colors of the compounds, which range from colorless with \(n = 1\), to orange with \(n = 2-7\), to red with \(n = 8\), as \(\lambda_\text{max}\) goes from the ultraviolet into the visible region of the electromagnetic spectrum.
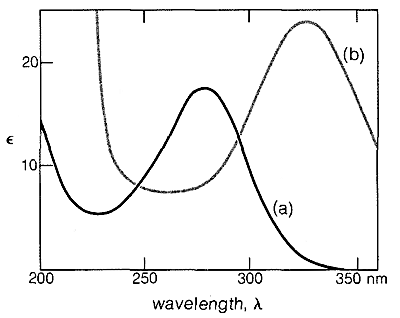
Similar effects are found with conjugated \(\ce{C=O}\) and \(\ce{C=N}\) double bonds. For example, the electronic spectra of 2-butanone and 3-buten-2-one are shown in Figure 9-20.
Conjugation also can influence infrared spectra. Transitions arising from \(C=C\) and \(C=O\) stretching vibrations generally are more intense and are shifted to slightly lower frequencies (longer wavelengths) for conjugated compounds relative to nonconjugated compounds. Thus the \(C=C\) stretching of 1-butene occurs at \(1650 \: \text{cm}^{-1}\), whereas that of 1,3-butadiene is observed at \(1597 \: \text{cm}^{-1}\).
Alkanes and cycloalkanes have no low-energy electronic transitions comparable to conjugated systems or molecules with nonbonding electrons. Therefore alkanes and cycloalkanes show no absorption above \(200 \: \text{nm}\) and are good solvents to use for electronic spectroscopy.
Applications of Electronic Spectroscopy
How do we use electronic spectroscopy in chemical analysis? The two principal applications are structure determinations and quantitative analysis. The position and intensity of an electronic absorption band provides information as to chemical structure. Such absorptions normally are not as useful as infrared absorptions because they do not give as detailed information. For our purposes here, the main points to remember are:
- A weak absorption (\(\epsilon = 10-100\)) suggests an \(n \rightarrow \pi^*\) transition of an isolated carbonyl group. If this absorption is found in the region \(270\)-\(350 \: \text{nm}\) an aldehyde or ketone is probable.
- Somewhat stronger absorptions (\(\epsilon = 100-4,000\)) between \(200 \: \text{nm}\) and \(260 \: \text{nm}\) may correspond to \(\pi \rightarrow \sigma^*\) transitions.
- Strong absorptions (\(\epsilon = 10,000-20,000\)) usually are characteristic of \(\pi \rightarrow \pi^*\) transitions. If absorption occurs above \(200 \: \text{nm}\), a conjugated system of multiple bonds is indicated. Each additional carbon-carbon double bond shifts \(\lambda_\text{max}\) about \(30 \: \text{nm}\) to longer wavelengths and enhances the intensity of absorption. Conjugation also shifts \(\lambda_\text{max}\) of \(n \rightarrow \pi^*\) transitions to longer wavelengths.
If we are dealing with compounds for which the wavelengths and the molar intensities of the absorption bands are known, then we can use the degree of absorption for quantitative analysis with the aid of the Beer-Lambert law (see Table 9-3 for definitions):
\[A = \epsilon cl\]
By measuring the absorbance \(A\) of a sample of known \(\epsilon\) in a cell of known path length \(I\), the concentration \(c\) may be determined. Because changes in absorbance reflect changes in concentration, it is possible to use absorbance measurements to follow rates of chemical reactions, to determine equilibrium constants (such as the dissociation constants of acids and bases), and to follow conformational changes in bio-organic molecules such as proteins and nucleic acids.
The capacity of electronic spectroscopy for performing qualitative and quantitative of the elements in chemical compounds has been done and applications have been made to elements of low atomic number, such as carbon and oxygen. Electronic spectra has been developed in the study of this elements and it’s compounds.
References
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


