6.5: Atomic-Orbital Models

Alkanes

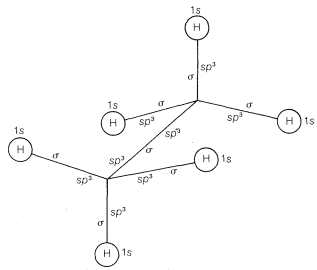
Saturated compounds such as the alkanes and their derivatives, which have normal tetrahedral angles for the bonds to carbon, can be formulated readily in terms of atomic orbitals with \(sp^3 \: \sigma\) bonds to carbon. An example is shown in Figure 6-11, which also shows how an atomic-orbital model can be drawn in abbreviated style. The lines in this drawing correspond to bonds and are labeled as \(sp^3\) with \(sp^3\) (the overlapping orbitals of the \(C-C\) bond) or as \(sp^3\) with \(s\) (the overlapping orbitals of the \(C-H\) bonds).

Atoms with Unshared Electron Pairs

Many important molecules such as ammonia, water, and hydrogen fluoride have atoms with unshared pairs of electrons:

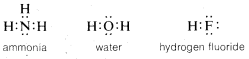
If we formulate each of these molecules in such a way to minimize repulsions between like charges, a basically tetrahedral arrangement will be expected because this will place the nuclei (and electron pairs) as widely separated as possible.

Figure 6-11: Abbreviated atomic-orbital model of ethane showing only the orbitals of the outer-shell electrons

The water molecule could be formulated this way, as in \(6\), with the oxygen at the center of the tetrahedron:

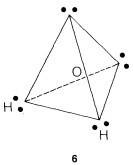
The simple picture predicts that the \(H-O-H\) bond angle should be tetrahedral, \(109.5^\text{o}\). But actually it is \(104.5^\text{o}\).

There are two schools of thought as to why the angle is \(104.5^\text{o}\). One idea is that the repulsion model is too simple and has to be modified to take into account that the repulsion is more severe between pairs of unshared electrons than between electrons in bonding orbitals on the same atom. This is because when a bond is formed between two nuclei, the attraction of the nuclei for the electrons shrinks the orbitals available to the bonding electrons, thereby reducing their electrostatic repulsion with other pairs. The degree of repulsion between electron pairs diminishes in the sequence: unshared pairs vs. unshared pairs \(>\) unshared pairs vs. bonding pairs \(>\) bonding pairs vs. bonding pairs. From this, we expect that in water the \(H-O-H\) angle will be less than tetrahedral, because the larger repulsion between the two unshared pairs will tend to push the bonding pairs closer together.

A similar, but smaller, effect is expected for ammonia because now the repulsion is only between the one unshared pair and bonding pairs. The ammonia \(H-N-H\) angle is \(107.3^\text{o}\), which is only slightly smaller than the tetrahedral value of \(109.5^\text{o}\).

The alternative point of view of why the bond angle of water is \(104.5^\text{o}\) starts with the premise that, in the simplest approximation, the angle should be \(90^\text{o}\)! To see how this comes about let us compare \(H:Be:H\) with \(H:\underset{\cdot \cdot}{\ddot{O}}:H\). You will recall that to form two bonds to \(Be\), we had to promote an electron and change the electronic configuration to the valence configuration, \(\left( 2s \right)^1 \left( 2p \right)^1\). The situation with \(H_2O\) is different in that the oxygen ground state and valence state are the same, \(\left( 2s \right)^2 \left( 2p_x \right)^1 \left( 2p_y \right)^1 \left( 2p_z \right)^1\). This means we could form two equivalent bonds to oxygen using the \(2p_y\) and \(2p_z\) orbitals at an angle of \(90^\text{o}\) (Figure 6-12).

Figure 6-12: Overlap of the hydrogen \(1s\) orbitals with \(2p_y\) and \(2p_z\) orbitals centered on oxygen. The \(p\) orbitals are represented here with distorted shapes to make the drawing clearer.

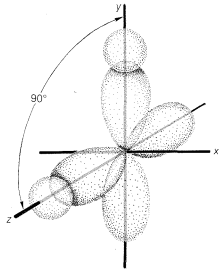
Now, to explain why the \(H-O-H\) bond angles are \(104.5^\text{o}\) instead of \(90^\text{o}\), we can say that the repulsion between the hydrogen nuclei is expected to widen the bond angle. An argument in favor of this formulation is provided by the bond angle in \(H_2S\), which is \(92.2^\text{o}\). This is much closer to the \(90^\text{o}\) expected for \(p\)-bond orbitals and the hydrogens in \(H_2S\) would not be expected to repel each other as much as in \(H_2O\) because sulfur is a larger atom than oxygen.

Both ways of formulating the orbitals used in the bonding of water molecules are in current use. Arguments can be advanced in favor of both. Highly sophisticated quantum-mechanical calculations, which we will say more about later, suggest that oxygen in water molecules uses orbitals that are \(18\% \: s\) and \(82\% \: p\) in its bonds (\(sp^{4.5}\)), and furthermore, that the unshared pairs are in equivalent hybrid orbitals [not one pair as \(\left( 2s \right)^2\) and the other as \(\left( 2p \right)^2\)]. Each of the unshared electron-pair orbitals of oxygen in water is calculated to be about \(40\% \: s\) and \(60\% \: p\) (\(sp^{1.5}\)).

The results are hardly clearcut, but the bonding orbitals are considerably closer to \(sp^3\) (\(25\% \: s\) and \(75\% \: p\)) than they are to \(100\% \: p\). We recommend that the bonding orbitals of nitrogen and oxygen be considered to be \(sp^3\) and the unshared pairs designated simply as \(\left( n \right)^2\). An abbreviated atomic orbital model of methanol, \(CH_3OH\), made on this basis is shown in Figure 6-13.

Figure 6-13: Abbreviated atomic-orbital model of methanol, \(CH_3OH\), showing the orbitals of the outer-shell electrons only

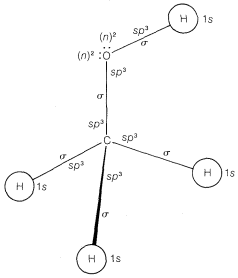
Compounds with Double Bonds

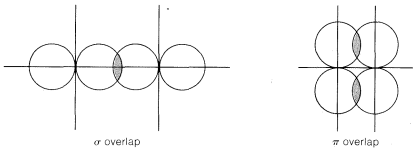
Recall from Chapter 2 that bond angles in compounds with carbon-carbon double bonds such as ethene are closer to \(120^\text{o}\) than to the normal tetrahedral value of \(109.5^\text{o}\). There are several way sin which a carbon-carbon double bond can be formulated in terms of atomic-orbital models. One very popular approach is to consider that ethene has two \(sp^2\)-hybridized carbons that form one carbon-carbon \(\sigma\) bond and four carbon-hydrogen \(\sigma\) bonds by overlap of the six \(sp^2\) orbitals, as shown in Figure 6-14. The remaining carbon-carbon bond is formulated as arising from sidewise overlap of the two \(p\) orbitals, one on each carbon, that are not utilized in making the \(sp^2\) hybrids. Sidewise overlap of \(p\) orbitals is called \(\pi\) overlap to distinguish it from the endwise \(\sigma\) overlap of the type we have discussed previously (Figure 6-15). The resulting \(\pi\) bond differs from the \(\sigma\) bond in that electron density is concentrated in the regions above and below the bond axis rather than along the bond axis.

Figure 6-14: The \(\sigma\)-\(\pi\) formulation of ethene

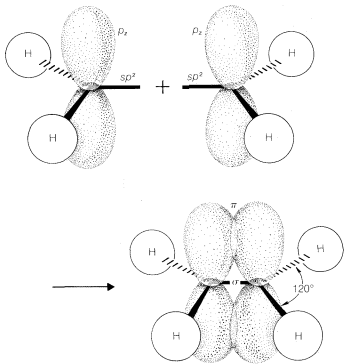
Formulations of ethene in this way suggests that it should be a planar molecule with \(H-C-H\) angles of \(120^\text{o}\). Ethene is indeed planar, but its \(H-C-H\) angles are found to be \(117^\text{o}\), rather than the \(120^\text{o}\) predicted for \(sp^2\) bonds. An explanation of this discrepancy using further electron-repulsion arguments will be discussed later in the chapter.

Figure 6-15: Schematic representation of \(\sigma\) overlap and \(\pi\) overlap of \(p\) orbitals

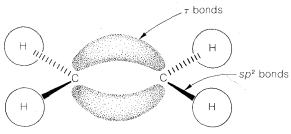
The simple elegance of the \(\sigma\)-\(\pi\) model of ethene should not be taken as proving that there actually are two different kinds of bonds between the carbons. The \(\sigma\)-\(\pi\) representation of double bonds is not really unique. Given \(sp^2\) hybridization of the carbons so there are \(sp^2\)-\(\sigma\) bonds to the hydrogens, it is possible to take the \(sp^2\) and \(p\) orbitals used for the \(\sigma\) and \(\pi\) bonds, rehybridize them, and so derive a new set of overlapping orbitals for the double bond. These orbitals are called \(\tau\) (tau) bonding orbitals and can be represented by two banana-shaped orbitals between the carbons (Figure 6-16). The result is two completely equivalent \(C-C\) bonds. The \(\tau\) model has the advantage of offering a striking parallel to ball-and-stick models, whereas the \(\sigma\)-\(\pi\) model is of particular value as a basis for quantitative calculations, as will be discussed in Chapter 21.

 

Figure 6-16: Formulation of ethene with \(\tau\) bonds. Each \(\tau\) orbital is considered to contain an electron pair.

Using the \(\sigma\)-\(\pi\) model of double bonds, we conclude that the twisted configuration shown in Figure 6-17 should not be very stable. Here the \(p\) orbitals are not in position to overlap effectively in the \(\pi\) manner. The favored configuration is expected to have the axes of the \(p\)-\(\pi\) orbitals parallel. Because considerable energy would have to be expended to break the \(p\)-\(\pi\) double bond and to permit rotation about the remaining \(sp^2\)-\(\sigma\) bond, restricted rotation and stable cis-trans isomers are expected. Similar conclusions can be reached on the basis of the \(\tau\) model of the double bond.

Figure 6-17: Orientation of \(p\) orbitals in twisted configuration of ethene

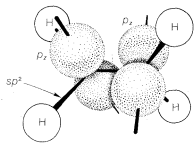
Compounds with Triple Bonds

Ethyne, \(C_2H_2\), is an organic compound that usually is formulated with \(sp\) hybrid bonds. The carbon-hydrogen framework is built up through \(\sigma\) overlap of two \(sp\)-hybrid orbitals, one from each carbon atom, to form a \(C-C\) bond, and \(\sigma\) overlap of the remaining \(sp\) orbitals with the \(s\) orbital of two hydrogens to form \(C-H\) bonds. The remaining two carbon-carbon bonds result through sidewise \(\pi\) overlap of the pure \(p\) orbitals, as shown in Figure 6-18. This model fits well with the properties of the ethyne molecule being linear (bond angles of \(180^\text{o}\). Also, the \(C-H\) bonds in ethyne are different from those in ethene or ethane, as judged by their \(C-H\) stretching and bending frequencies in the

Figure 6-18: The \(\sigma\)-\(\pi\) formulation of ethyne

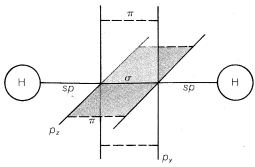
infrared (Chapter 9), their bond energies, (Table 4-6), and their acidities (Section 11-8). These differences in properties are in keeping with the different states of hybridization of the carbon orbitals that we have postulated for ethane, ethene, and ethyne.

More on Hybrid Bond Orbitals and Molecular Geometry

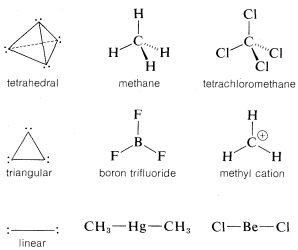
A summary of the directional character of the \(s\)-\(p\) hybrid atomic orbitals discussed so far is given in Table 6-2. By referring to this table, it usually is possible to deduce the nature of the bonding orbitals for most organic compounds from the molecular geometry, if this is known, Thus a tetrahedral molecule \(AX_4\) with four attached ligands uses \(sp^3\) hybrid orbitals localized on atom \(A\); a planar triangular molecule \(AX_3\) with three attached ligands at angles of \(120^\text{o}\) is \(sp^2\) hybridized at atom \(A\); a linear molecule \(AX_2\) with two ligands is \(sp\) hybridized at \(A\).

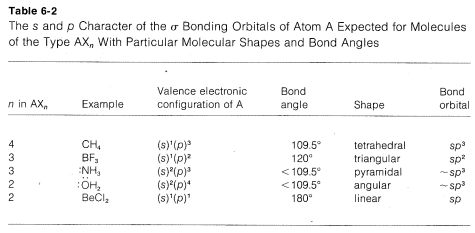
Applying the converse of these rules, one should be able to predict molecular geometry by making reasonable assumptions as to the state of hybridization for each atom in the molecule. Obviously in doing this we have to take account of unshared electron pairs. Prediction is easy if unshared pairs are absent. Thus, four attached ligands, as in \(CH_4\), \(CCl_4\), or \(BF_4^\ominus\), imply \(sp^3\) hybridization at the central atom and therefore a tetrahedral arrangement of ligands. Three ligands, as bonded to carbon in \(CH_3^\oplus\) or to boron in \(BF_3\), imply \(sp^2\) hybridization for the central atom and a planar triangular arrangement if ligands. Two ligands, as in \(CO_2\), imply \(sp\) hybridization and linear geometry.

In many of our later discussions of organic reactions, we will be concerned with cationic, radical, and anionic carbon species that are substitution products of \(CH_3^\oplus\), \(CH_3 \cdot\), and \(CH_3:^\ominus\). Because of the importance of these entities, you should know how to formulate them and related substances, such as \(^\ominus: \ddot{N}H_2\), with atomic orbitals. Perhaps the most straightforward way is to start from \(CH_4\) and see what changes in the \(C-H\) bonds we would expect as the result of the hypothetical processes: \(CH_4 \rightarrow CH_3:^\ominus + H^\oplus\), \(CH_4 \rightarrow CH_3^\oplus + H:^\ominus\), and \(CH_4 \rightarrow CH_3 \cdot + H \cdot\).

Methane is tetrahedral with \(sp^3\) carbon bonding orbitals. Removal of \(H^\oplus\) gives \(CH_3:^\ominus\), which corresponds in electronic structure to \(H_3N:\) and, for the same reasons, should have a pyramidal shape with nearly tetrahedral \(H-C-H\) angles. Removal of \(H:^\ominus\) from \(CH_4\) to give \(CH_3^\oplus\) with six bonding electrons, suggests a change to \(sp^2\) bonding orbitals for the carbon and planar geometry with \(H-C-H\) angles of \(120^\text{o}\).

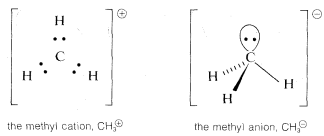
The radical, \(CH_3 \cdot\) presents a special problem. We can think of it as being formed by the loss of \(H \cdot\) from \(CH_4\), by adding an electron to planar \(CH_3^\oplus\), or by removing an electron from pyramidal \(CH_3:^\ominus\). We can formulate \(CH_3 \cdot\) with \(Sp^2\) orbitals for the \(C-H\) bonds and the extra electron in a \(p\) orbital, or with \(sp^3\) orbitals for the \(C-H\) bonds and the extra electron in an \(sp^3\) orbital:

The actual structure of \(CH_3 \cdot\) has the hydrogens and carbons in a plane (left). Therefore it appears that the repulsions between the bonding electron pairs is greater than the repulsions between the extra electron and the bonding pairs. The actual structure corresponds to the one in which the bonding pairs are as far apart as possible.

More on Interelectronic Repulsion and Bond Angles

Molecules of the type \(AX_4\), which have four identical ligands on the central atom and no unshared electrons on \(A\) (e.g., \(CH_4\) and \(CCl_4\)), are expected to be, and are, tetrahedral. By the same reasoning, three electron pairs around one atom should seek a planar arrangement with \(120^\text{o}\) angles to minimize electron repulsion; accordingly, species of the type \(AX_3\), which have no unshared pairs on \(A\) (e.g., \(BF_3\) and \(CH_3^\oplus\)), have this geometry. With only two electron pairs, the preferred arrangement is linear.

The bond angles of compounds with multiple bonds can be explained similarly. For example, in ethene the four electrons of the double bond occupy the region in space between the two carbon nuclei. The situation at either carbon is rather like the \(AX_3\) case, except that one of the ligands now has a double complement of bonding electrons:

Therefore the carbon orbitals are expected to be directed in one plane to give bond angles that deviate somewhat from \(120^\text{o}\) because of the high density of electrons in the multiple bond. Thus the \(H-C-H\) angle shrinks to \(117^\text{o}\), whereas the \(H-C=C\) angles open up to \(122^\text{o}\), because repulsion between electrons in the \(H-C=C\) bonds is greater than between electrons in the \(H-C-H\) bonds.

Electron-attracting power (or electronegativity) of the ligands also is important in determining bond angles. Thus for compounds of the type \(CH_3X\), in which \(X\) is a more electron-attracting group than carbon, the \(C-X\) bond is polarized in the sense \(H_3 \overset{\delta \oplus}{C} - - - \overset{\delta \ominus}{X}\), and the carbon then should have some of the character of \(CH_3^\oplus\). Thus the \(H-C-H\) angles are expected to be greater than \(109.5^\text{o}\), as in fact they are. In chloromethane, for example, the \(H-C-H\) angle is \(111^\text{o}\).

Also, we can explain on the basis of electron repulsions why the bond angle in phosphine, \(:PH_3\) (\(93^\text{o}\)), is less than that in ammonia, \(:NH_3\) (\(107.3^\text{o}\)), and the bond angle in \(H: \underset{\cdot \cdot}{\ddot{S}} :H\) (\(92.2^\text{o}\)) is less than that in \(H: \underset{\cdot \cdot}{\ddot{O}}\) (\(104.5^\text{o}\)). The important point is that phosphorus and sulfur are larger atoms than nitrogen and oxygen. This means than the \(H-S-H\) and \(H-P-H\) bond angles can be about \(90^\text{o}\) without bringing the hydrogens and the bonding pairs as close together as they are in \(H_2O\) and \(NH_3\) where the bond angles are near to the tetrahedral value.

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."