6.4: Electron Repulsion and Bond Angles. Orbital Hybridization

In predicting bond angles in small molecules, we find we can do a great deal with the simple idea that unlike charges produce attractive forces while like charges produce repulsive forces. We will have electron-nuclear attractions, electron-electron repulsions, and nucleus-nucleus repulsions. Let us first consider the case of a molecule with just two electron-pair bonds, as might be expected to be formed by combination of beryllium and hydrogen to give beryllium hydride, \(H:Be:H\). The problem will be how to formulate the bonds and how to predict what the \(H-Be-H\) angle, \(\theta\), will be:

Figure 6-5):

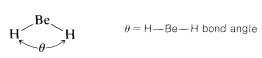
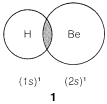
We might formulate a second \(\sigma\) bond involving the \(2p\) orbital, but a new problem arises as to where the hydrogen should be located relative to the beryllium orbital. Is it as in \(2\), \(3\), or some other way?

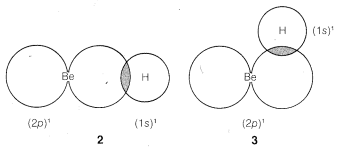
The \(Be\) and \(H\) nuclei will be farther apart in \(2\) than they will be in \(3\) or any other similar arrangement, so there will be less internuclear repulsion with \(2\). We therefore expect the hydrogen to locate along a line going through the greatest extension of the \(2p\) orbital.

According to this simple picture, beryllium hydride should have two different types of \(H-Be\) bonds - one as in \(1\) and the other as in \(2\). This is intuitively unreasonable for such a simple compound. Furthermore, the \(H-Be-H\) bond angle is unspecified by this picture because the \(2s\) \(Be\) orbital is spherically symmetrical and could form bonds equally well in any direction.

However, if we forget about the orbitals and only consider the possible repulsions between the electron pairs, and between the hydrogen nuclei, we can see that these repulsions will be minimized when the \(H-Be-H\) bond angle is \(180^\text{o}\). Thus arrangement \(5\) should be more favorable than \(4\), with a \(H-Be-H\) angle less than \(180^\text{o}\):

Unfortunately, we cannot check this particular bond angle by experiment because \(BeH_2\) is unstable and reacts with itself to give a high-molecular-weight solid. However, a number of other compounds, such as \(\left( CH_3 \right)_2 Be\), \(BeCl_2\), \(\left( CH_3 \right)_2 Hg\), \(HgF_2\), and \(\left( CH_3 \right)_2 Zn\), are known to have \(\sigma\) bonds involving \(\left( s \right)^1 \left( p \right)^1\) valence states. Measurements of the bond angles at the metal of these substances in the vapor state has shown them to be uniformly \(180^\text{o}\).

Figure 6-7: Representation of the relative sizes of \(2s\) and \(2p\) orbitals

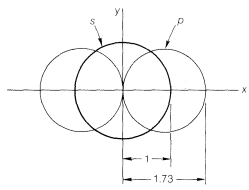
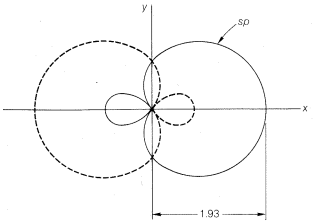
How are the \(s\) and \(p\) orbitals deployed in this kind of bonding? It turns out that stronger bonds are formed when the degree of overlap of the orbitals is high. The degree of overlap will depend on the sizes of the orbital and, particularly, on how far out they extend from the nucleus. Figure 6-7 shows how far \(2s\) and \(2p\) orbitals extend relative to one another. Bonding with these orbitals as in \(1\) and \(2\) does not utilize the overlapping power of the orbitals to the fullest extent. With \(1\) we have overlap that uses only part of the \(2s\) orbital, and with \(2\), only a part of the \(2p\) orbital. Molecules such as \(BeH_2\) can be formulated with better overlap and equivalent bonds with the aid of the concept of orbital hybridization. This concept, published independently by L. Pauling and J. C. Slater in 1931, involves determining which (if any) combinations of \(s\) and \(p\) orbitals may overlap better and make more effective bonds than do the individual \(s\) and \(p\) orbitals. The mathematical procedure for orbital hybridization predicts that an \(s\) and a \(p\) orbital of one atom can form two stronger covalent bonds if they combine to form two new orbitals called \(sp\)-hybridized orbitals (Figure 6-8). Each \(sp\)-hybrid orbital has an overlapping power of 1.93, compared to the pure \(s\) orbital taken as unity and a pure \(p\) orbital as 1.73. Bond angles of \(180^\text{o}\) are expected for bonds to an atom using \(sp\)-hybrid orbitals and, of course, this also is the angle we expect on the basis of our consideration of minimum electron-pair and internuclear repulsions. Henceforth, we will proceed on the basis that molecules of the type \(X:M:X\) may form \(sp\)-hybrid bonds.

Figure 6-8: Diagram of two \(sp\) hybrid orbitals composed of an \(s\) orbital and a \(p\) orbital. One of the orbitals (solid line) has its greatest extension in the plus \(x\) direction, while the other orbital (dotted line) has its greatest extension in the minus \(x\) direction. Bonds utilizing both of these \(sp\) orbitals would form at an angle of \(180^\text{o}\).

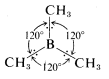
On the basis of repulsion between electron pairs and between nuclei, molecules such as \(BH_3\), \(B \left( CH_3 \right)_3\), \(BF_3\), and \(AlCl_3\), in which the central atom forms three covalent bonds using the valence-state electronic configuration

\(\left( s \right)^1 \left( p_x \right)^1 \left( p_y \right)^1\), are expected to be planar with bond angles of \(120^\text{o}\). For example,

Figure 6-9). These \(sp^2\) orbitals have their axes in a common plane and are at \(120^\text{o}\) to one another. The predicted overlapping power is 1.99.

Figure 6-9: Diagram of three \(sp^2\) hybrid orbitals made from an \(s\) orbital, a \(p_x\) orbital, and a \(p_y\) orbital. Each orbital is shown with a different kind of line.

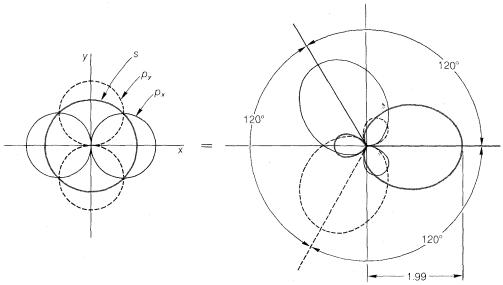
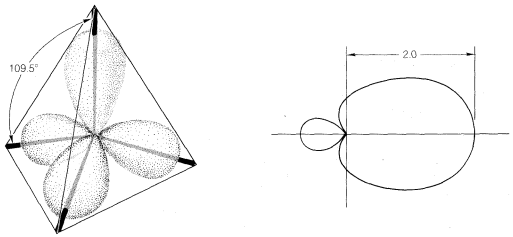
With atoms such as carbon and silicon, the valence-state electronic configuration to form four covalent bonds has to be \(\left( s \right)^1 \left( p_x \right)^1 \left( p_y \right)^1 \left( p_z \right)^1\). Repulsion between the electron pairs and between the attached nuclei will be minimized by formation of a tetrahedral arrangement of the bonds. the same geometry is predicted from hybridization one one \(s\) and three \(p\) orbitals, which gives four \(sp^3\)-hybrid orbitals directed at angles of \(109.5^\text{o}\) to each other. The predicted relative overlapping power of \(sp^3\)-hybrid orbitals is 2.00 (Figure 6-10).

 

Figure 6-10: Diagram of the \(sp^3\) hybrid orbitals

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."

Template:HideTOC