6.6: Resonance
- Page ID
- 22186
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
An Atomic-Orbital Model of Benzene
Until now, we have discussed bonding only in terms of electron pair associated with two nuclei. These we may call localized electrons. In fact, bonding electrons can be associated with more than two nuclei, and there is a measure of stability to be gained by this because the degree of bonding increases when the electrons can distribute themselves over a greater volume. This effect often is called electron delocalization or resonance. It is important only if the component atomic orbitals overlap significantly, and this will depend in large part on the molecular geometry.
The classic example of resonance is provided by the \(\pi\) bonding of benzene. This compound was shown in Chapter 1 to have the molecular formula \(C_6H_6\), to be planar, and hexagonal with bond angles of \(120^\text{o}\), and to possess six equivalent \(C-C\) bonds and six equivalent \(C-H\) bonds. Benzene usually is written with a structural formula proposed by Kekulé:
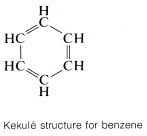
That benzene is more stable than a single Kekulé, or 1,3,5-cyclohexatriene, structure can be gauged by comparing the experimental heat of combustion
of benzene with the calculated value based on the average bond energies of Table 4-3:
\[\ce{C6H6(g) + 15/2 O2 -> 6CO2(g) + 3H2O(g)}\]
with
\[\begin{aligned}
&\Delta H_{\exp }^{0}=-789 \mathrm{kcal} \\
&\Delta H_{\text {calc }}^{0}=-827 \mathrm{kcal}
\end{aligned}\]
About \(38 \: \text{kcal}\) less energy is released on combustion than calculated. Benzene, therefore, is \(38 \: \text{kcal mol}^{-1}\) more stable than the cyclohexatriene structure predicts.
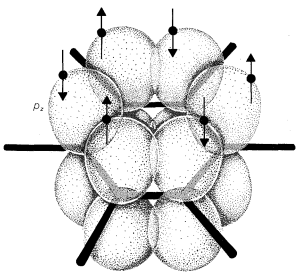
Representation of Resonance
Atomic-orbital models, like that shown for benzene, are useful descriptions of bonding from which to evaluate the potential for electron delocalization. But they are cumbersome to draw routinely. We need a simpler representation of electron delocalization.
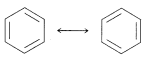
The method that commonly is used is to draw a set of structures, each of which represents a reasonable way in which the electrons (usually in \(p\) orbitals) could be paired. If more than one such structure can be written, the actual molecule, ion, or radical will have properties corresponding to some hybrid of these structures. A double-headed arrow \(\leftrightarrow\) is written between the structures that we consider to contribute to the hybrid. For example, the two Kekulé forms are two possible electron-pairing schemes or valence-bond structures that could contribute to the resonance hybrid of benzene:
It is very important to know what attributes a reasonable set of valence-bond structures has to have to contribute to a hybrid structure. It is equally important to understand what is and what is not implied in writing a set of structures. Therefore we shall emphasize the main points to remember in the rest of this section.
1. The members of a set of structures, as the two Kekulé structures for benzene, have no individual reality. They are hypothetical structures representing different electron-pairing schemes. We are not to think of benzene as a 50:50 mixture of equilibrating Kekulé forms.
2. To be reasonable, all structures in a set representing a resonance hybrid must have exactly the same locations of the atoms in space. For example, formula \(7\) does not represent a valid member of the set of valence-bond structures of benzene, because the atoms of \(7\) have different positions from those of benzene (e.g., \(7\) is not planar):
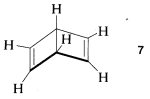
Structure \(7\) actually represents a known \(C_6H_6\) isomer that has a very different chemistry from that of benzene.
3. All members of the set must have the same number of paired or unpaired electrons. For the normal state of benzene, the six \(\pi\) electrons have three of one spin and three of the other. Structures such as \(8\), with four electrons of one spin and two of the other, are not valid contributors to the ground state of benzene:
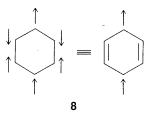
4. The importance of resonance in any given case will depend on the energies of the contributing structures. The lower and more nearly equivalent the members of the set are in energy, the more important resonance becomes. That is to say, electron stabilization is greatest when there are two or more structures of lowest energy (as for the two Kekulé structures of benzene). As a corollary, the structure of a molecule is least likely to be satisfactorily represented by a conventional structural formula when two (or more) energetically equivalent, low-energy structures may be written.
5. If there is only one low-energy structure in the set then, to a first approximation, the resonance hybrid may be assigned properties like those expected for that structure. As an example, we show three possible pairing schemes for ethene, \(9\), \(10\), and \(11\):

Although \(10\) and \(11\) are equivalent, they are much higher in energy than \(9\) (see discussion in Section 4-4C). Therefore they do not contribute substantially to the structure of ethene that is best represented by \(9\).
Resonance is by no means restricted to organic molecules. The following sets of valence-bond structures represent the hybrid structures of nitrate ion, \(NO_3^\ominus\), carbonate ion \(CO_3^{2 \ominus}\), and nitrous oxide, \(N_2O\). These are only representative examples. We suggest that you check these structures carefully to verify that each member of a set conforms to the general rules for resonance summarized above.
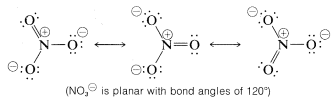
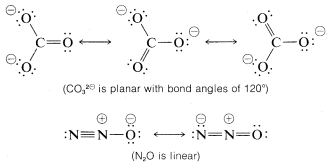
A shorthand notation of hybrid structures frequently is used in which the delocalized \(\pi\)-bonding is shown as a broken line. For benzene, an inscribed circle also is used to indicate continuous \(\pi\) bonding:
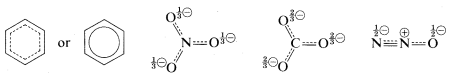
Resonance and Reactivity
Electron delocalization is an important factor in the reactivity (or lack of it) of organic molecules. As an example, recall from Chapter 4 that the bond energies of various types of \(C-H\) bonds differ considerably (see Table 4-6). In particular, the methyl \(C-H\) bond in propene is about \(9 \: \text{kcal}\) weaker than the methyl \(C-H\) bond of ethane or propane, and this difference can be explained by the use of the resonance concept. The following bond dissociations are involved:

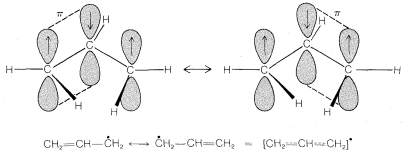
delocalization is possible for the propyl radical, propane, or propene. Accordingly, the methyl \(C-H\) bond strength in propene is less than in propane because of stabilization of the 2-propenyl radical.
The foregoing discussion adds further to our understanding of the selectivity observed in the halogenation reactions discussed in Chapter 4. When propene is chlorinated in sunlight, the product is 3-chloropropene, and we may explain this on the basis that the radical-chain reaction involves propagation steps in which a chlorine atom attacks the hydrogen corresponding to the weakest \(C-H\) bond:
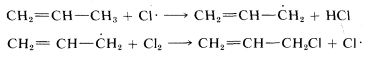
The resonance theory is very useful in accounting for, and in many cases predicting, the behavior of substances with \(\pi\) bonds. However, it is not omnipotent. One example where it fails is cyclobutadiene, for which we can write two equivalent valence-bond structures corresponding to the Kekulé structures for benzene:
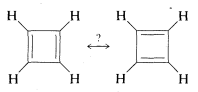
Despite this, cyclobutadiene is an extremely unstable substance, reacting with itself almost instantly at temperatures above \(-250^\text{o}\). For better understanding of this and some related problems, we provide a more detailed discussion of electron delocalization in Chapter 21.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


