28.2: Light Absorption, Flourescence, and Phosphorescence
- Page ID
- 22388
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Electromagnetic radiation in the ultraviolet and visible region spans a wavelength range of about \(800\)-\(100 \: \text{nm}\) corresponding to energies of \(36\)-\(286 \: \text{kcal mol}^{-1}\). Absorption of such radiation by molecules is not to be regarded as equivalent to simple excitation by thermal energy of \(36\)-\(286 \: \text{kcal mol}^{-1}\). Instead, all the energy of the light quantum is taken up in excitation of an electron to a high-energy, usually antibonding, orbital (Section 9-9). An important point about such processes is that they occur more rapidly than the atoms vibrate in the bonds (Franck-Condon principle). The short transition time of an electron between ground and excited states is in complete contrast to what happens during absorption of a quantum of radio-frequency energy in nmr spectroscopy, wherein the absorption process may be slow compared to chemical reactions (Section 27-1). Therefore an electronically excited molecule is, in the first instant that it is produced \(\left( <10^{-13} \: \text{sec} \right)\), just like the ground-state molecule as far as positions and kinetic energies of the atoms go, but has a very different electronic configuration. What happens at this point depends on several factors, some of which can be best illustrated by energy diagrams of the type used previously (Section 21-1). We shall consider diatomic molecules, but the argument can be extended to more complicated systems.
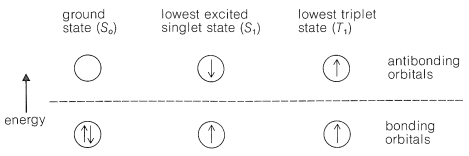
Consider Figure 28-1, which shows schematic potential-energy curves for a molecule \(\ce{A-B}\) in the ground state \(\left( \ce{A-B} \right)\) and in excited electronic states \(\left( \ce{A-B} \right)^*\). We have noted previously (Section 6-1) that in the ground states of most molecules all electrons are paired; excited states also can have all electrons paired. Such states with paired electrons are called singlet states. But, because the bonding is weaker in excited states, the average bond length \(r_e\) between the nuclei is greater in the excited state than in the ground state. For this reason the upper curve \(\left( S_1 \right)\) in Figure 28-1 is displaced toward a larger average bond length relative to the lower or ground-state curve \(\left( S_0 \right)\).
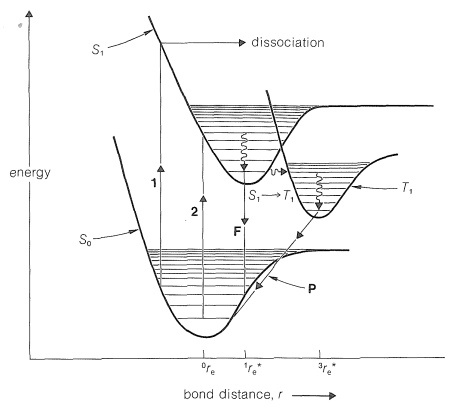
Excited states also can have unpaired electrons. States with two unpaired electrons are called triplet states \(\left( T \right)\) and normally are more stable than the corresponding singlet states because, by Hund's rule, less interelectronic repulsion is expected with unpaired than paired electrons (Sections 6-1 and 21-9A). (For clarity, the potential-energy curve for the excited triplet state \(\left( T_1 \right)\) of \(\ce{A-B}\) is given an unrealistically long equilibrium bond distance, which puts it to the right of the curve for the \(S_1\) state in Figure 28-1.) The electronic configurations for ground singlet \(\left( S_0 \right)\), excited singlet \(\left( S_1 \right)\), and triplet \(\left( T_1 \right)\) states of the \(\sigma\) electrons of a diatomic molecule are shown in Figure 28-2. This diagram will be helpful in interpreting the transitions between \(S_0\), \(S_1\), and \(T_1\) states shown in Figure 28-1, and which we will now discuss in more detail.
When a molecule absorbs sufficient radiant energy to cause electronic excitation, the spin of the excited electron remains unchanged in the transition. That is to say, ground-state molecules with paired electrons \(\left( S_0 \right)\) give excited states with paired electrons \(\left( S_1 \right)\), not triplet states \(\left( T_1 \right)\). The transition marked \(1\) in Figure 28-1 corresponds to a singlet-singlet \(\left( S_0 \rightarrow S_1 \right)\) transition from a relatively high vibrational level of \(\ce{A-B}\). The energy change occurs with no change in \(r\) (Franck-Condon principle), and the electronic energy of the \(\ce{A-B}^*\) molecule so produced is seen to be above the level required for dissociation of \(\ce{A-B}^*\). The vibration of the excited molecule therefore has no restoring force and leads to dissociation to \(\ce{A}\) and \(\ce{B}\) atoms. In contrast, the transition marked \(2\) leads to an excited vibrational state of \(\ce{A-B}^*\), which is not expected to dissociate but can lose vibrational energy to the surroundings and come down to a lower vibrational state. This is called "vibrational relaxation" and usually requires about \(10^{-12} \: \text{sec}\). The vibrationally "relaxed" excited state can return to the ground state with emission of radiation (transition \(F\), \(S_1 \rightarrow S_0\)); this is known as fluorescence, the wavelength of fluorescence being different from that of the original light absorbed. Normally, fluorescence, if it occurs at all, occurs in \(10^{-9}\) to \(10^{-7} \: \text{sec}\) after absorption of the original radiation.
In many cases, the excited state \(\left( S_1 \right)\) can return to the ground state \(\left( S_0 \right)\) by nonradiative processes. The most important processes are:
1. By chemical reaction, often with surrounding molecules. This process forms the basis of much organic photochemistry, which will be described in a later section.
2. By transfer of its excess electronic energy to other molecules. This kind of energy transfer also is a very important aspect of photochemistry, and we shall return to it shortly.
3. By decay through a lower energy state. If, for example, the potential-energy curves for the upper and lower singlet states were closer together than shown in Figure 28-1, they may actually cross at some point, thus providing a pathway for \(S_1\) to relax to \(S_0\) without fluorescing. But what about decay of \(S_1\) through the triplet state \(\left( T_1 \right)\)?
Conversion of a singlet excited state to a triplet state \(\left( S_1 \rightarrow T_1 \right)\) is energetically favorable but usually occurs rather slowly, in accord with the spectroscopic selection rules, which predict that spontaneous changes of electron spin should have very low probabilities. Nonetheless, if the singlet state is sufficiently long-lived, the singlet-triplet change, \(S_1 \rightarrow T_1\), (often called intersystem crossing) may occur for a very considerable proportion of the excited singlet molecules.
The triplet state, like the singlet state, can return to the ground state by nonradiative processes, but in many cases a radiative transition \(\left( T_1 \rightarrow S_0 \right)\) occurs, even though it has low probability. Such transitions result in emission of light of considerably longer wavelength than either that absorbed originally or resulting from fluorescence. This type of radiative transition is called phosphorescence (transition \(P\) in Figure 28-1). Because phosphorescence is a process with a low probability, the \(T_1\) state may persist from fractions of a second to many seconds. For benzene at \(-200^\text{o}\), the absorption of light at \(254 \: \text{nm}\) leads to fluorescence centered on \(290 \: \text{nm}\) and phosphorescence at \(340 \: \text{nm}\). The half-life of the triplet state of benzene at \(-200^\text{o}\) is \(7 \: \text{sec}\).
The Carbonyl Group
In previous discussions of electronic absorption spectra (Section 9-9), we have identified two different kinds of transitions in the spectra of simple carbonyl compounds such as 2-propanone or methanal. One involves excitation of an electron in a nonbonding \(n\) orbital on oxygen to an antibonding \(\left( \pi^* \right)\) orbital of the carbon-oxygen double bond (an \(n \rightarrow \pi^*\) transition), and the other involves excitation of an electron in the bonding \(\left( \pi \right)\) orbital to the corresponding antibonding orbital (a \(\pi \rightarrow \pi^*\) transition). These changes are shown for methanal in Figure 28-3. Besides the transitions already discussed, methanal shows strong absorption at \(175 \: \text{nm}\), which possibly is \(n \rightarrow \sigma^*\), or else \(\sigma \rightarrow \sigma^*\).
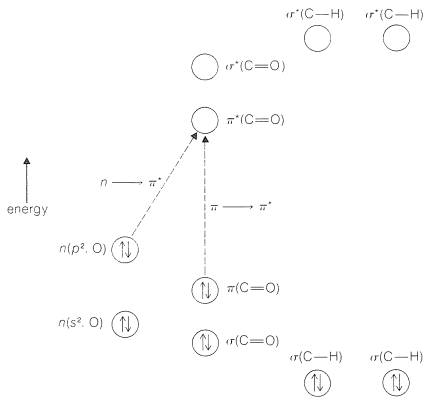
Although the \(n \rightarrow \pi^*\) and \(\pi \rightarrow \pi^*\) transitions of Figure 28-3 are singlet-singlet transitions, each of the two singlet excited states produced has a corresponding triplet state. Accordingly, there are four easily accessible excited states of a carbonyl group - the \(n \rightarrow \pi^*\) singlet \(\left( S_1 \right)\), \(n \rightarrow \pi^*\) triplet \(\left( T_1 \right)\), \(\pi \rightarrow \pi^*\) singlet \(\left( S_2 \right)\), and \(\pi \rightarrow \pi^*\) triplet \(\left( T_2 \right)\). The energies of these electronic states for methanal decrease in the order \(S_2 > T_2 > S_1 > T_1\), although this ordering may not hold for all carbonyl compounds.
As we shall see, \(n \rightarrow \pi^*\) singlet and triplet states of carbonyl compounds play an important role in photochemistry. Aldehydes and ketones display all the characteristics of absorption, fluorescence, phosphorescence, and intersystem crossing \(\left( S_1 \rightarrow T_1 \right)\) illustrated in Figure 28-1. Generally, they are more efficient at intersystem crossing than are unsaturated hydrocarbons, perhaps because the energies of the \(S\) and \(T\) states involved are not widely different.
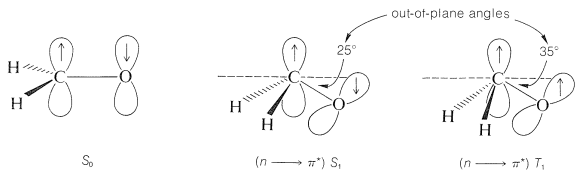
Besides the bond lengths being longer in excited states of molecules, the molecular shapes differ from those of the ground states. Although the Franck-Condon principle requires that absorption produce excited states with the same geometry as the ground states, the excited molecules thereafter can relax to more stable shapes, which may be nonplanar and twisted about the erstwhile \(\pi\) bonds. Methanal is planar with a \(\ce{C-O}\) bond length of \(1.21 \: \text{Å}\) in the ground state, but in the \(n \rightarrow \pi^*\) singlet \(\left( S_1 \right)\) state, methanal is pyramidal, with a \(\ce{C-O}\) bond length of \(1.32 \: \text{Å}\). Methanal is even more distorted in the \(n \rightarrow \pi^*\) triplet state, although the bond length remains about the same at \(1.32 \: \text{Å}\).
Indirect Electronic Excitation Energy Transfer
It is possible to produce electronic excited states of molecules indirectly by way of energy transfer from other excited molecules. An example is provided by excitation of naphthalene as the result of energy transfer from excited benzophenone. Benzophenone, \(\ce{C_6H_5COC_6H_5}\), absorbs ultraviolet light with \(\lambda_\text{max} = 330 \: \text{nm}\) in an \(n \rightarrow \pi^*\) transition. Naphthalene does not absorb appreciably in this region. Yet irradiation of a mixture of benzophenone and naphthalene with \(330\)-\(\text{nm}\) light produces phosphorescent emission from naphthalene. Thus benzophenone absorbs the light and transfers its excess energy to naphthalene, which returns to the ground state by emission. Because the emission is from the triplet state of naphthalene, benzophenone must be involved in exciting the naphthalene to the triplet state. We may write the process as follows:
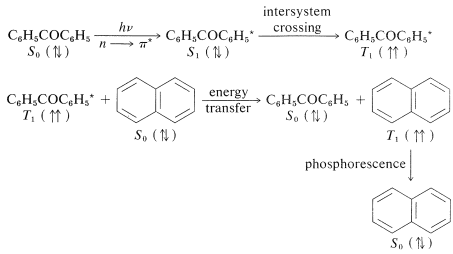
Energy transfer does not involve a net change in electron spin. For this to hold for excitation of naphthalene from \(S_0\) to \(T_1\), the energy transfer must come from triplet (not singlet) benzophenone). The process of producing excited states in this way is called photosensitization. Singlet-singlet, as well as triplet-triplet, energy transfers are possible, but in all cases there is no net change in spin. Efficient energy transfer will only be possible if \(\Delta G^0\) for the transfer is small or negative.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


