9.8: Infrared (Rovibrational) Spectroscopy
- Page ID
- 22225
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)At the turn of the nineteenth century Sir William Herschel discovered invisible radiation beyond the red end of the visible region of the electromagnetic spectrum. This radiation appropriately is called infrared, meaning “beneath the red,” and it encompasses the wavelength region from \(10^3 \: \text{nm}\) to \(10^6 \: \text{nm}\). You probably are familiar with the common applications of infrared to radiant heating and photography. In addition to these uses, infrared spectroscopy has become the most widely used spectroscopic technique for investigating organic structures.
Infrared spectroscopy was the province of physicists and physical chemists until about 1940. At that time, the potential of infrared spectroscopy as an analytical tool began to be recognized by organic chemists. The change was due largely to the production of small, quite rugged infrared spectrophotometers and instruments of this kind now are virtually indispensable for chemical analysis. A brief description of the principles and practice of this spectroscopic method is the topic of this section.
General Considerations of Infrared Spectroscopy
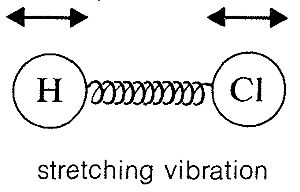
Absorption of infrared radiation causes transitions between vibrational energy states of a molecule. A simple diatomic molecule, such as \(\ce{H-Cl}\), has only one vibrational mode available to it, a stretching vibration somewhat like balls on the ends of a spring:
Molecules with three or more atoms can vibrate by stretching and also by bending of the chemical bonds, as indicated below for carbon dioxide:
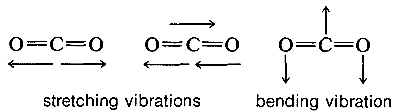
The absorption frequencies in the infrared spectra of molecules correspond to changes in the stretching or bending vibrations or both. In general, a polyatomic molecule with \(n\) atoms will have \(3n - 6\) modes of vibration of which \(n -1\) are stretching vibrations and \(2n - 5\) are bending vibrations. There are circumstances, however, where fewer vibrational modes are possible. If the molecule is linear, like \(CO_2\), then there are \(3n-5\) possible vibrations, and some of these vibrations may be equivalent (degenerate vibrations in the language of spectroscopists). For example, \(CO_2\) should have \(3n - 5\) or \(4\) vibrational modes, two of which are stretching and two of which are bending modes. However, the two bending modes are equivalent because the direction in which the molecule bends is immaterial; in-plane or out-of-plane bending are the same:
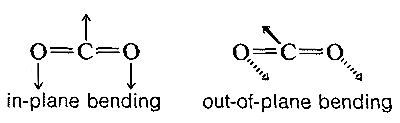
Diatomic molecules such as \(HCl\) have one vibrational mode, but it is important to note that symmetrical diatomic molecules, such as \(O_2\), \(N_2\), \(Cl_2\), \(F_2\), and \(H_2\), do not absorb in the infrared region of the spectrum. This is because absorption cannot occur if the vibration is electrically symmetrical. Fortunately, then, the infrared spectra can be recorded in air because the main components of air, \(N_2\) and \(O_2\), do not interfere.
In practice, infrared spectra can be obtained with gaseous, liquid, or solid samples. The sample containers (cells) and the optical parts of the instrument are made of rock salt (\(NaCl\)) or similar material that transmits infrared radiation (glass is opaque).
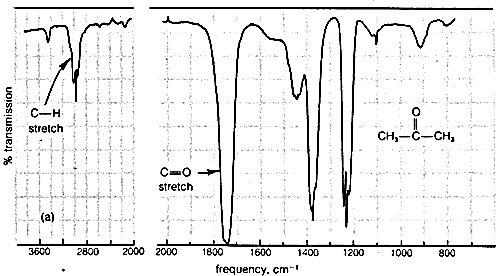
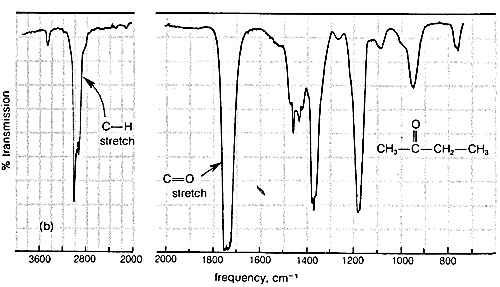
Typical infrared spectra are shown in Figure 9-9 for 2-propanone (acetone), \(\ce{CH_3-CO-CH_3}\), and 2-butanone (methyl ethyl ketone), \(\ce{CH_3-CO-CH_2-CH_3}\). In accord with current practice, the position of absorption (horizontal scale) is recorded in units of wave numbers (\(\bar{\nu}\), \(\text{cm}^{-1}\); see Section 9-3). The vertical scale measures the intensity of radiation transmitted through the sample. Zero transmission means complete absorption of radiation by the sample as at \(1740 \: \text{cm}^{-1}\) in Figure 9-9. The other absorption bands in Figure 9-9 that correspond to excitation of stretching or bending vibrations are not as intense as the absorption at \(1740 \: \text{cm}^{-1}\).
Characteristic Stretching Vibrations of Infrared Spectroscopy
What information can we derive about molecular structure from the vibrational bands of infrared spectra? Absorption of radiation in the range of \(5000\)-\(1250 \: \text{cm}^{-1}\) is characteristic of the types of bonds present in the molecule, and corresponds for the most part to stretching vibrations. For example, we know that the \(\ce{C-H}\) bonds of alkanes and alkyl groups have characteristic absorption bands around \(2900 \: \text{cm}^{-1}\); an unidentified compound that shows absorption in this region will very likely have alkane-type \(\ce{C-H}\) bonds.
More explicitly, the band observed for 2-propanone (Figure 9-9a) at \(3050 \: \text{cm}^{-1}\) arises from absorption of infrared radiation, which causes transitions between the ground vibrational state (or lowest vibrational energy level) of a \(\ce{C-H}\) bond and the first excited vibrational energy level for stretching of that \(\ce{C-H}\) bond. The band at \(1740 \: \text{cm}^{-1}\) corresponds to the infrared absorption that causes transitions between vibrational energy levels of the \(\ce{C=O}\) bond. The reason that these are transitions from the vibrational ground state is because, at room temperature, by far the largest portion of the molecules are in this state (cf. Exercise 9-9).
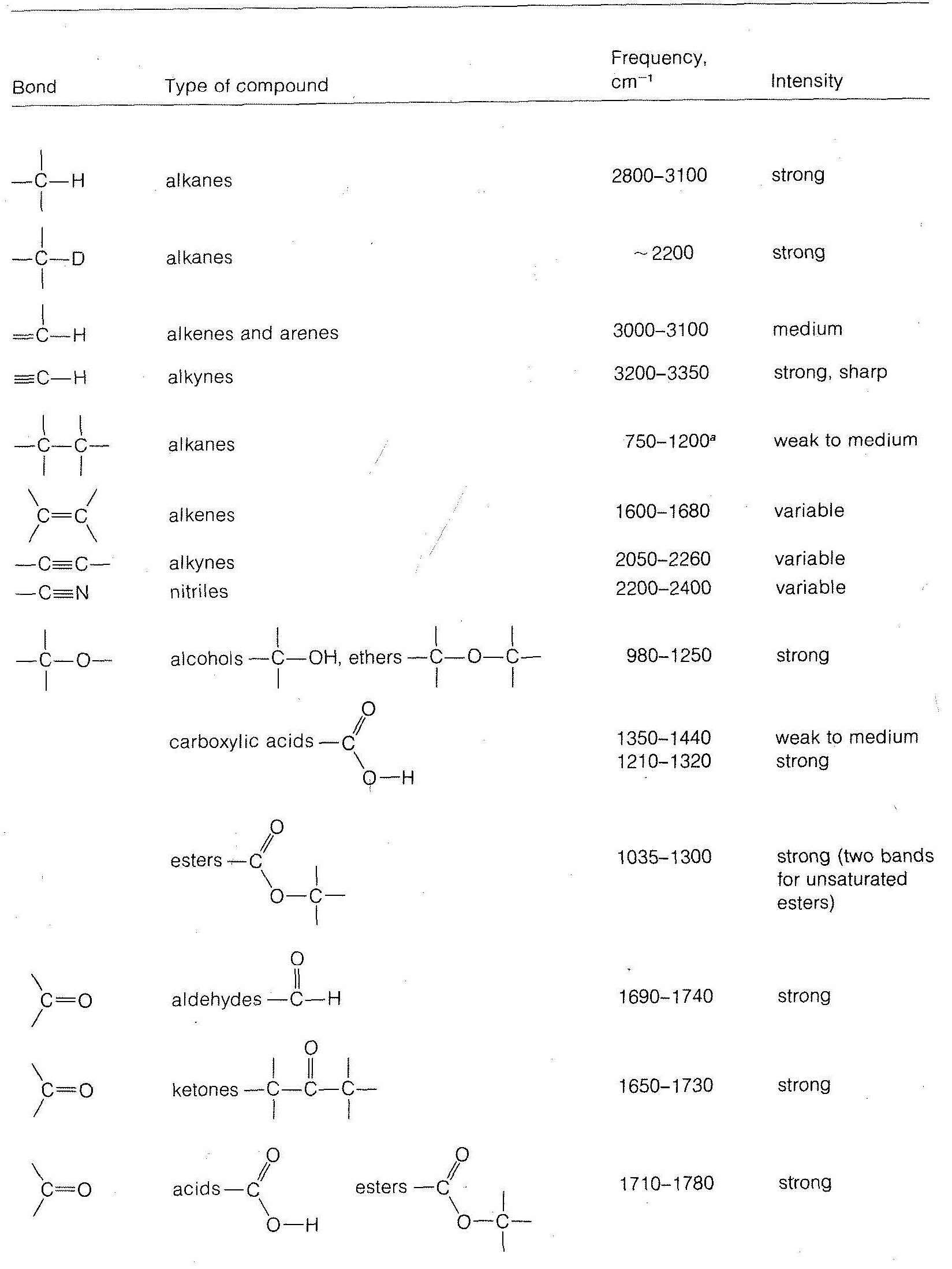
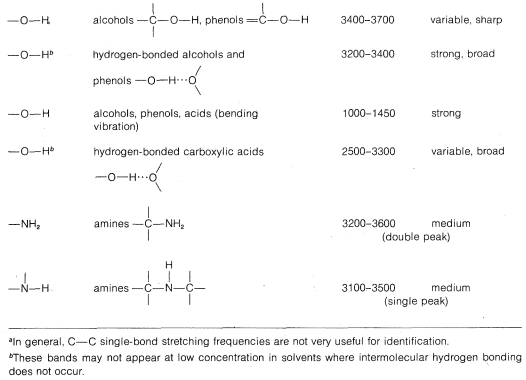
Stretching frequencies characteristic of the most important types of bonds found in organic molecules are given in Table 9-2. You will notice that the absorption band for each bond type is described by its position within a more or less broad frequency range and by its shape (broad, sharp) and intensity (strong, medium, weak).
A qualitative discussion of the factors that determine infrared band position and band intensities follows. To a first approximation, a chemical bond resembles a mechanical spring that vibrates with a stretching frequency \(\bar{\nu}\) (\(\text{cm}^{-1}\)),
\[ \bar{\nu} = \dfrac{1}{2\pi c} \sqrt{\dfrac{k}{\dfrac{m_1m_2}{m_1+m_2}}} \tag{9.3}\]
in which \(k\) is the force constant, and \(m_1\) and \(m_2\) are the masses of the individual atoms at each end of the bond. The force constant \(k\) is a measure of the stiffness of the bond and usually is related to the bond strength. From Equation 9-3, we can see that the heavier the bonded atoms, the smaller will be the vibrational frequency of the bond provided \(k\) remains essentially constant.\(^6\) Thus if we increase \(m_2\) while holding \(k\) and \(m_1\) constant we expect the frequency to decrease. This is just what occurs when we change the \(C-H\) bond to a \(C-D\) bond. We also see that the frequency decreases in the order \(\ce{C-H}\) > \(\ce{C-C}\) > \(\ce{C-N}\) > \(\ce{C-O}\), which also is in the order of increasing \(m_2\), but here matters are more complicated because \(k\) also changes.
Other things being equal, it requires more energy to stretch a bond than to bend it. Therefore the infrared bands arising from changes in the stretching vibrations are found at higher frequencies than are those arising from changes in the bending vibrations.
Another consequence of Equation 9-3 is that if \(m_1\) and \(m_2\) remain the same, the larger the value of \(k\), the higher will be the vibrational frequency. Because \(k\) is expected to run more or less parallel to the bond strength, and because multiple bonds are stronger than single bonds, the absorption frequencies of multiple bonds are higher than for single bonds. Examples are the absorption of \(C=C\) at \(2100 \: \text{cm}^{-1}\), \(C=C\) at \(1650 \: \text{cm}^{-1}\), and \(C-C\) at \(1000 \: \text{cm}^{-1}\).
Other effects besides mass and bond strength also affect infrared absorption frequencies. The structural environment of a bond is particularly important. Thus the absorption frequency of a \(\ce{C-H}\) bond depends on whether it is an alkyl, alkenyl, alkynyl, or aryl \(\ce{C-H}\) bond (see Table 9-2).
The intensity of an infrared absorption band arising from changes in the vibrational energy is related to the electrical symmetry of the bond. More symmetrical, less polarized bonds give weaker absorptions. In fact, if the bond is completely symmetrical, there is no infrared absorption. In contrast, unsymmetrical molecules in which the bonds are quite polarized, such as \(C=O\) bonds, show strong infrared absorptions.
Notice in Figure 9-9 that infrared spectra of organic molecules do not show very sharp absorption lines. This is because changes in rotational energies can occur together with the vibrational changes. The reason can be seen more clearly in Figure 9-10, in which each vibrational level, such as \(E_1\) and \(E_2\), of a molecule has associated with it closely spaced rotational levels. Transitions between \(E_1\) and \(E_2\) also may involve changes in rotational levels. This gives a “band” of closely spaced lines for any given vibrational change. For complex molecules, particularly in the liquid state, the “rotational fine structure” of a given vibrational band usually cannot be resolved.
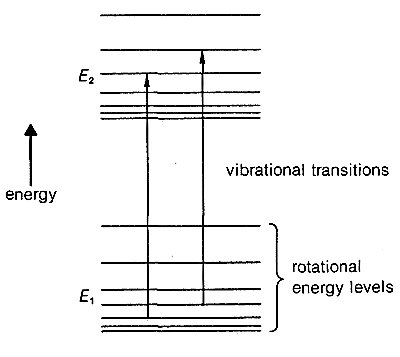
Table 9-2: Some Characteristic Infrared Absorption Frequencies
The Fingerprint Region
Infrared absorption bands between \(1250 \: \text{cm}^{-1}\) and \(675 \: \text{cm}^{-1}\) generally are associated with complex vibrational and rotational energy changes of the molecule as a whole and are quite characteristic of particular molecules. This part of the spectrum is often called the "fingerprint" region and is extremely useful for determining whether the samples are chemically identical. The spectra of 2-propanone and 2-butanone are seen to be very similar in the region \(4000 \: \text{cm}^{-1}\) to \(1250 \: \text{cm}^{-1}\) but quite different from \(1250 \: \text{cm}^{-1}\) to \(675 \: \text{cm}^{-1}\). The fingerprint region of the spectrum is individual enough so that if the infrared spectra of two samples are indistinguishable in the range of frequencies from \(3600 \: \text{cm}^{-1}\) to \(675 \: \text{cm}^{-1}\), it is highly probable that the two samples are of the same compound (or the same mixture of compounds).
Characteristic stretching and bending frequencies occur in the fingerprint region, but they are less useful for identifying functional groups, because they frequently overlap with other bands. This region is sufficiently complex that a complete analysis of the spectrum is seldom possible.
Alkanes and Cycloalkanes
The infrared spectra of the alkanes show clearly absorptions corresponding to the \(C-H\) stretching frequencies at \(2850 \: \text{cm}^{-1}\) to \(3000 \: \text{cm}^{-1}\). The \(C-C\) stretching absorptions have variable frequencies and are usually weak. Methyl (\(CH_3-\)) and methylene (\(-CH_2-\)) groups normally have characteristic \(C-H\) bending vibrations at \(1400 \: \text{cm}^{-1}\) to \(1470 \: \text{cm}^{-1}\). Methyl groups also show a weaker band near \(1380 \: \text{cm}^{-1}\). Two sample infrared spectra that illustrate these features are given in Figure 9-11.
The infrared spectra of the cycloalkanes are similar to those of the alkanes, except that when there are no alkyl substituents the characteristic
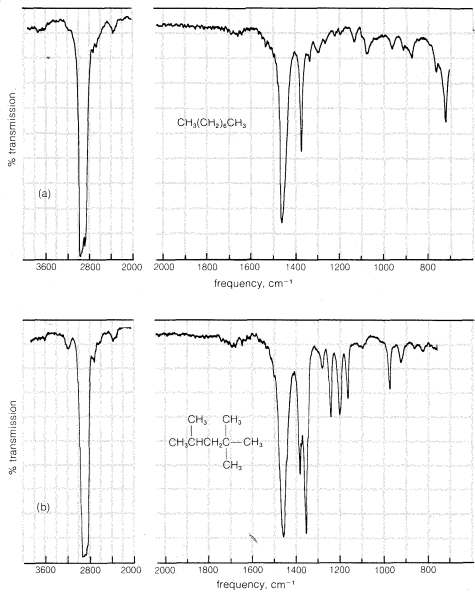
bending frequencies of methyl groups at \(1380 \: \text{cm}^{-1}\) are absent. A moderately strong \(CH_2\) "scissoring" frequency is observed between \(1440 \: \text{cm}^{-1}\) and \(1470 \: \text{cm}^{-1}\), the position depending somewhat on the size of the ring. These features of the infrared spectra of cycloalkanes are illustrated in Figure 9-12 using cyclooctane and methylcyclohexane as examples.

Applications of Infrared Spectroscopy to Structure Determination
Infrared spectra are very useful both for identification of specific organic compounds, and for determining types of compounds. For example, Figure 9-13 shows the infrared spectrum of a substance, \(C_4H_6O_2\), for which we wish to determine the compound type and, if possible, the specific structure. The most informative infrared absorptions for determining the compound type are between \(1500 \: \text{cm}^{-1}\) and \(3600 \: \text{cm}^{-1}\). Two groups of bands in this region can be seen at about \(1700 \: \text{cm}^{-1} \left( s \right)\) and \(3000 \: \text{cm}^{-1} \left( s \right)\), where \(\left( s \right)\) means strong; if we used \(\left( m \right)\) it would mean medium, and \(\left( w \right)\) would mean weak. From Table 9-2 we can see that these bands are indicative of \(C=O\) (\(1700 \: \text{cm}^{-1}\)) and hydrogen-bonded \(OH\) of carboxylic acids (\(3000 \: \text{cm}^{-1}\)). The presumption is that there is a \(-CO_2H\) group in the molecule, and we can derive some reassurance from the fact that the molecular formula \(C_4H_6O_2\) has enough oxygens to allow for this possibility.
Table 9-2 also shows that a \(-CO_2H\) group should have a \(C-O\) absorption band between \(1350 \: \text{cm}^{-1}\) and \(1400 \: \text{cm}^{-1}\) and \(O-H\) absorption (bending frequency) between \(1000 \: \text{cm}^{-1}\) and \(1410 \: \text{cm}^{-1}\), and there is indeed a band of medium intensity at \(1350 \: \text{cm}^{-1}\) and a strong band at \(1240 \: \text{cm}^{-1}\). These absorptions, being in the fingerprint region, do not prove that the compound is a carboxylic acid; but if there were no absorptions in the \(1000 \: \text{cm}^{-1}\) to \(1400 \: \text{cm}^{-1}\) range, the presence of a \(-CO_2H\) group would be highly questionable.
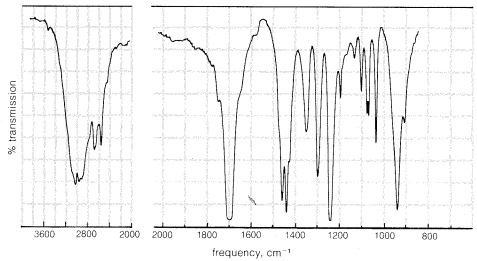
Tentatively, then, we may write a partial structure for \(C_4H_6O_2\) as


Final identification may be possible by comparison with an authentic spectrum of cyclopropanecarboxylic acid, if it is available in one of the several standard compendia of infrared spectra. A total of about 150,000 infrared spectra are available for comparison purposes. You should check with the reference section of your library to see what atlases of spectral data are available to you.
The foregoing example illustrates the way structures can be determined from infrared spectral data. For many purposes, the infrared frequencies given in Table 9-2 are both approximate and incomplete. However, you could be easily frustrated in interpreting spectral data by being burdened with a very detailed table in which the unimportant is mixed with the important. The ability to use extensive tables effectively comes with experience. You should remember that tabulated infrared frequencies indicate only the range in which a given vibrational transition will fall. The exact value for a particular compound usually is meaningless because it will change depending on whether the spectrum is taken of the solid, liquid, or gaseous states, the solvent used, the concentration, and the temperature.
\(^6\)Remember that lower frequency means longer wavelengths and lower energy.
References
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


