21.6: Application of MO Theory to Other Systems

Polar Molecules

Many important molecules have alternating single and double bonds (are conjugated), but have atoms that are more (or less) electron-attracting than carbon. An example is propenal (acrolein), \(18\):

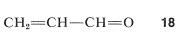
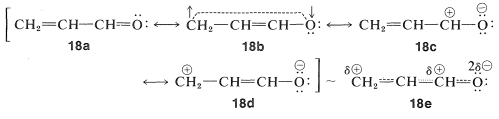
With such molecules we need to take into account the fact that the \(\pi\) electrons will be attracted to oxygen from carbon, because oxygen is more electronegative than carbon. With the VB method we can do this by considering ionic electron-pairing schemes, \(18c\) and \(18d\), along with the dienelike structures, \(18a\) and \(18b\). The hybrid, \(18e\), is drawn to reflect the expected relative contributions of the various forms, with \(18a\) being most important.

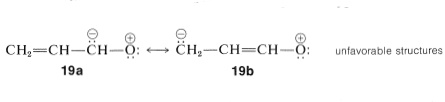
Ionic structures such as \(19a\) and \(19b\) need not be considered for propenal because carbon is much less electron-attracting than oxygen:

Figure 21-7, but with a greater contribution of the \(p\) orbital of oxygen in the lower bonding molecular orbitals:

Analysis of the electronic configuration resulting from the MO calculations accords generally with the VB hybrid \(18e\).

The 2-Propenyl (Allyl) Cation

An especially important type of carbocation is represented by the 2-propenyl electron-pairing schemes, \(21a\) and \(21b\), which correspond to the hybrid \(21c\).

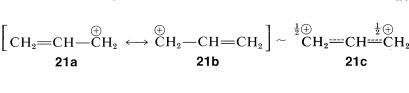
Because \(21a\) and \(21b\) are equivalent and no other single low-energy structure is possible, a sizable delocalization energy is expected. Evidence for this delocalization energy of \(21c\) is available from the comparative ease of reactions involving formation of carbocation intermediates. An example is in \(S_\text{N}1\) ionizations of alkenyl and alkyl halides. The ionization \(\ce{CH_2=CHCH_2Br} \rightarrow \ce{CH_2=CHCH_2^+} + \ce{Br^+}\) proceeds more readily than \(\ce{CH_3CH_2CH_2Br} \rightarrow \ce{CH_3CH_2CH_2^+} + \ce{Br^+}\) (for which no \(\pi\)-electron delocalization is possible).

MO treatment of the 2-propenyl cation begins with the atomic-orbital model \(22\):

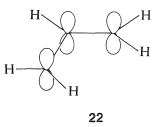
Any \(\pi\) electrons will be delocalized through the orbitals of \(22\), but it is not so easy to be confident that when two electrons are placed into the lowest molecular orbital the resulting electron distribution will be the same as \(21c\) with half of the positive charge on \(\ce{C_1}\) and half on \(\ce{C_3}\).

The complete calculation gives the result shown in Figure 21-9. Here the lowest-energy molecular orbital has a higher proportion of the \(p\) orbital of \(\ce{C_2}\) mixed in than the \(p\) orbitals of \(\ce{C_1}\) and \(\ce{C_3}\) - in fact, just the right amount to have \(\ce{C_2}\) neutral and \(\ce{C_1}\) and \(\ce{C_3}\) each with \(\frac{1}{2}^\oplus\) when this MO is filled with two paired electrons. The delocalization energy calculated for the cation is \(\left( 2 \alpha + 2.82 \beta \right) - \left( 2 \alpha + 2 \beta \right) = 0.82 \beta\) or about \(16 \: \text{kcal}\) if \(\beta\) is taken to be \(19 \: \text{kcal}\). Thus in every respect the simple VB and MO methods give the same representation of the 2-propenyl carbocation.

Figure 21-9: Energies and schematic representations of the \(\pi\) molecular orbitals of the 2-propenyl cation, \(22\). The calculated \(\pi\)-electron energy of the cation is \(2 \left( \alpha + 1.41 \beta \right) = 2 \alpha + 2.82 \beta\). Orbitals with the energy \(\alpha\) are neither bonding nor antibonding and are called "nonbonding molecular orbitals" (NBMO). The intermediate energy molecular orbital of the 2-propenyl cation is a NBMO because its component atomic orbitals, being on \(\ce{C_1}\) and \(\ce{C_3}\), are too far apart to be bonding or antibonding.

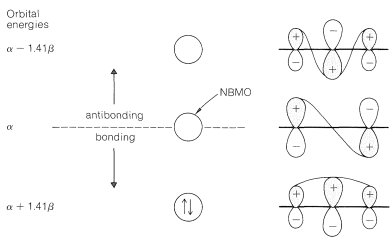
You will notice that the 2-propenyl radical and the 2-propenyl carbanion can be formulated by the same set of \(\pi\) molecular orbitals (Figure 21-9) used for the carbocation by putting one or two electrons into the nonbonding MO. The delocalization energies calculated for the radical and anion are the same as for the cation. Thus \(\left( 3 \alpha + 2.82 \beta \right) - \left( 3 \alpha + 2 \beta \right) = 0.82 \beta\) for the radical and \(\left( 4 \alpha + 2.82 \beta \right) - \left( 4 \alpha + 2 \beta \right) = 0.82 \beta\) for the anion.

Electronic Spectra by the MO Method

Section 9-9B covers qualitative explanations of how the VB method is used to account for the lower-energy (longer-wavelength) radiation required for electron excitation of conjugated polyenes compared to nonconjugated polyenes. Thus 1,3-butadiene has a \(\lambda_\text{max}\) for ultraviolet light at \(217 \: \text{nm}\), whereas 1,5-hexadiene has a corresponding \(\lambda_\text{max}\) at \(185 \: \text{nm}\).

We will now consider how the MO approach can be used to understand these differences in excitation energy. The \(\pi\)-energy levels and electronic configurations for delocalized and localized 1,3-butadiene are shown in Figure 21-10 (also see Section 21-4). Because the double bonds are so far apart, the \(\pi\)-electron system of 1,5-hexadiene by the simple MO approach is identical with that of localized 1,3-butadiene. The calculated energy change for the lowest-energy \(\pi \rightarrow \pi^*\) transition is \(\left( \alpha - 0.62 \beta \right) - \left( \alpha + 0.6 \beta \right) = -1.24 \beta\) for 1,3-butadiene and \(\left( \alpha - \beta \right) - \left( \alpha + \beta \right) = -2 \beta\) for 1,5-hexadiene. In each case the energy of the electron in the highest occupied \(\pi\) orbital (the HOMO orbital) is subtracted from the energy that an electron would have in the lowest unoccupied \(\pi^*\) orbital (the LUMO orbital). Other transitions are possible, as of an electron from the lowest occupied orbital of energy \(\alpha + 1.62 \beta\) to the highest unoccupied orbital of energy \(\alpha - 1.62 \beta\), but these would have far greater energies.

Figure 21-10: The \(\pi\)-molecular-orbital energies and ground-state electronic configurations of (left) delocalized 1,3-butadiene and (right) localized 1,3-butadiene or 1,5-hexadiene.

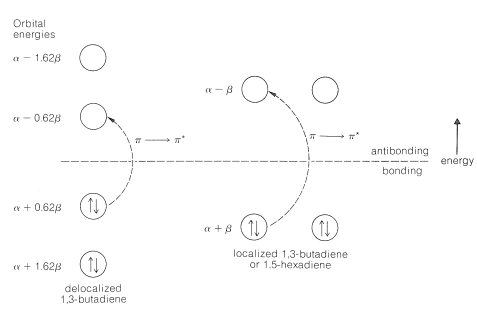
Qualitatively, the \(\pi \rightarrow \pi^*\) transition energy is predicted to be substantially less for 1,3-butadiene than for 1,5-hexadiene. However, any attempt at a quantitative correlation is suspect, because the lowest energy \(\pi \rightarrow \pi^*\) transition calculated for 1,3-butadiene is \(-1.24 \beta\) and, if \(\beta\) is \(19 \: \text{kcal}\) (see Section 21-3C), \(\lambda_\text{max}\) from Equation 9-2 should be \(1214 \: \text{nm}\) instead of the observed \(217 \: \text{nm}\).

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."