21.4: The Benzene Problem

We already have alluded to the difficulties encountered in the interpretation of the structure of benzene in Sections 1-1G and 6-5. Our task here is to see what new insight the VB and MO treatments can give us about benzene, but first we will indicate those properties of benzene that are difficult to explain on the basis of simple structure theory.

Some of the Unusual Properties of Benzene

From x-ray diffraction and spectroscopic measurements, benzene is known to be a planar molecule with six carbons \(1.390\) Å apart in a hexagonal ring, \(5\). Six hydrogen atoms, one associated with each carbon, are located \(1.09\) Å from those carbons. All \(\ce{H-C-C}\) and \(\ce{C-C-C}\) bond angles are \(120^\text{o}\):

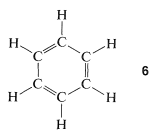
The 1,3,5-cyclohexatriene structure, \(6\), proposed for benzene in 1866 by Kekule, has alternating single and double bonds around the ring, which would be predicted to have bond lengths of \(1.48\) Å and \(1.34\) Å, respectively (see Table 2-1):

The knowledge that the bond lengths are equal in the ring in benzene is a point against the Kekule formulation, but a more convincing argument is available from a comparison of the chemistry of benzene with that of 1,3,5-hexatriene, \(7\):

Figure 21-4. The reagents that commonly add (in the dark) to the double bonds of alkenes (e.g., \(\ce{Br_2}\), \(\ce{Cl_2}\), \(\ce{HOCl}\), \(\ce{H_2SO_4}\)) attack benzene relatively slowly to substitute for a hydrogen atom rather than to give addition products. Nevertheless, there can be no doubt that benzene is really saturated, because it can be hydrogenated (under forcing conditions compared with simple alkenes) to cyclohexane, and, in sunlight, adds chlorine or bromine to give 1,2,3,4,5,6-hexahalocyclohexanes. Also, benzene is attacked by ozone, and the products are those expected on the basis of Kekule's cyclohexatriene structure.

Figure 21-4: Comparative reactions of benzene and 1,3,5-hexatriene.

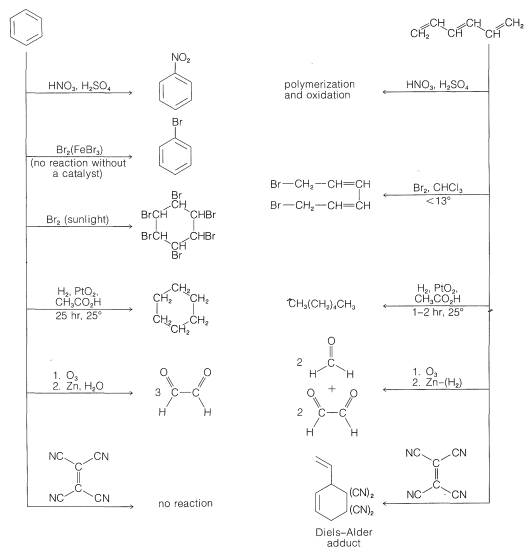
Benzene also is more stable by about \(36\)-\(38 \: \text{kcal mol}^{-1}\) than anticipated for the 1,3,5-cyclohexatriene structure. You will recall from earlier discussions that the heat of combustion of one mole of benzene is \(38 \: \text{kcal}\) less than calculated for cyclohexatriene (see Section 6-5A). Also, the heat of hydrogenation of benzene is only \(49.8 \: \text{kcal mol}^{1}\), which is \(36 \: \text{kcal}\) less than expected for 1,3,5-cyclohexatriene; this estimate is based on the assumption that the heat of hydrogenation of 1,3,5-cyclohexatriene (with three double bonds) would be three times that of cyclohexane (\(28.5 \: \text{kcal mol}^{-1}\), for one double bond), or \(3 \times 28.2 = 85.5 \: \text{kcal mol}^{-1}\).

The extra stability of benzene relative to the hypothetical 1,3,5-cyclohexatriene can be called its stabilization energy. Most (but not all) of this stabilization may be ascribed to resonance or electron delocalization.

The Atomic-Orbital Model of Benzene

In Section 6-5 an atomic model of benzene was discussed in some detail. Each carbon in the ring was considered to form three coplanar \(sp^2\)-hybrid \(\sigma\) bonds at \(120^\text{o}\) angles. These carbon-carbon and carbon-hydrogen \(\sigma\) bonds use three of the four valence electrons of each carbon. The remaining six carbon electrons are in parallel \(p\) orbitals, one on each of the six carbons. Each of the \(\pi\) electrons can be regarded as being paired with its immediate neighbors all around the ring, as shown by \(8\):

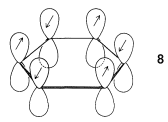
As mentioned in Section 21-2B, delocalization of the electrons over all six centers in benzene should give a more stable electron distribution than any structure in which the electrons are localized in pairs between adjacent carbons (as in the classical 1,3,5-cyclohexatriene structure).

The simple MO and VB treatments of benzene begin with the same atomic-orbital model and each treats benzene as a six-electron \(\pi\)-bonding problem. The assumption is that the \(\sigma\) bonds of benzene should not be very much different from those of ethene and may be regarded as independent of the \(\pi\) system.

The Molecular Orbital Method for Benzene

Extension of the ideas of Section 21-2 for the MO treatment of an electron-pair bond between two nuclei to the \(\pi\) bonding in benzene is fairly straightforward. What is very important to understand is that there must be more than one molecular orbital for the \(\pi\) electrons because there are six \(\pi\) electrons, and the Pauli principle does not allow more than two paired electrons to occupy a given orbital. In fact, combination (or mixing) os the six \(2p\) orbitals of benzene, shown in \(8\), gives six \(\pi\) molecular orbitals. Without exception, the number of molecular orbitals obtained by mixing is always the same as the number of atomic orbitals mixed. The details of the mathematics of the mixing process to give an optimum set of molecular orbitals will not be described here,\(^1\) but the results are shown in Figure 21-5. Of the six predicted molecular orbitals, three are bonding and three are antibonding. The six \(\pi\) electrons are assigned to the three bonding orbitals in pairs and are calculated to have a total \(\pi\)-electron energy of \(6 \alpha + 8 \beta\).

Figure 21-5: Energies and schematic representation of the \(\pi\) molecular orbitals of benzene. If the six \(\pi\) electrons are placed in the three lowest orbitals in three pairs, the \(\pi\)-electron energy is \(2 \left( \alpha + 2 \beta \right) + 4 \left( \alpha + \beta \right) = 6 \alpha + 8 \beta\), in which \(\alpha\) and \(\beta\) are negative energy terms. The schematic representations are drawn to show the phase changes (nodes) of the molecular orbitals. Notice that the more phase changes there are, the less bonding and more antibonding the orbital becomes. Although one could hardly believe it by looking at the schematic representations of the occupied \(\pi\) orbitals, the mathematical form of these is such that benzene is predicted to have its \(\pi\) electrons symmetrically distributed with an average of one per carbon atom. That is, the total \(\pi\)-electron distribution is the same as that suggested by the lowest-energy, nodeless molecular orbital.

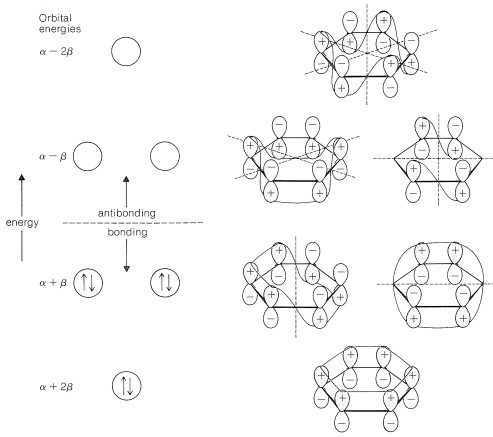
The calculation that leads to the results shown in Figure 21-5 is not very sophisticated. It is based on the assumption that the \(\pi\) bonding between each carbon and its immediate neighbors is equal all around the ring and that bonding involving carbons more than \(2\) Å apart is unimportant.

What happens if we use the MO method to calculate the \(\pi\)-electron energy of classical 1,3,5-cyclohexatriene? The procedure is exactly as for benzene, except that we decree that each carbon \(p\) orbital forms a \(\pi\) bond with only one of its neighboring \(p\) orbitals. The results are shown in Figure 21-6. The \(\pi\)-electron energy turns out to be three times that of ethene, or \(6 \alpha + 6 \beta\) compared to \(6 \alpha + 8 \beta\) for benzene.

Figure 21-6: Energies and schematic representations of the \(\pi\) molecular orbitals of localized 1,3,5-cyclohexatriene. The molecular orbitals are the \(\pi\) orbitals of three localized ethene bonds and the total \(\pi\)-electron energy is \(6 \left( \alpha + \beta \right) = \left( 6 \alpha + 6 \beta \right)\).

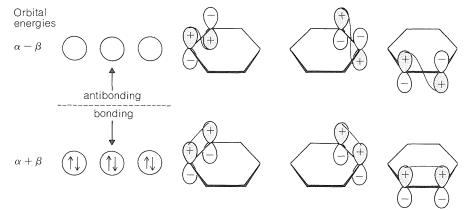
The calculated delocalization energy for benzene is the difference between these quantities, or \(\left( 6 \alpha + 8 \beta \right) - \left( 6 \alpha + 6 \beta \right) = 2 \beta\). That is to say, the calculated delocalization energy is the difference between the energy of benzene with full \(\pi\) bonding and the energy of 1,3,5-cyclohexatriene with alternating single and double bonds. If the electron delocalization energy \(\left( 2 \beta \right)\) is equal to the stabilization energy \(\left( 38 \: \text{kcal mol}^{-1} \right)\), then \(\beta = 19 \: \text{kcal mol}^{-1}\). Whether this is a valid method for determining \(\beta\) has been a matter of dispute for many years. Irrespective of this, the results of the calculations do account for the fact that benzene is more stable than would be expected for 1,3,5-cyclohexatriene.

However, do the results also account for the low reactivity toward the various reagents in Figure 214, such as those that donate \(\ce{Br}^\oplus\) to double bonds (see Section 10-3A)? To settle this question, we have calculated the changes in \(\pi\)-electron energy that occur in each of the following reactions:

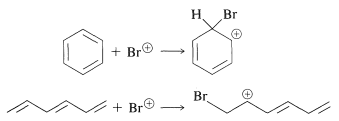
This means calculating the \(\pi\)-electron energies of all four entities and assuming that the differences in the \(\sigma\)-bond energies cancel between the two reactions. The result of this rather simple calculation is that attack of \(\ce{Br}^\oplus\) on benzene is thermodynamically less favorable than on 1,3,5-cyclohexatriene by about \(\beta\). If \(\beta\) is \(19 \: \text{kcal mol}^{-1}\), this is clearly a sizable energy difference, and we can conclude that the simple MO method does indeed account for the fact that benzene is attacked by \(\ce{Br}^\oplus\) far less readily than is 1,3,5-cyclohexatriene.

The Valence Bond Method for Benzene

Extension of the basic ideas of the VB treatment described in Section 21-2 to the atomic-orbital model of benzene is straightforward. We can write VB structures that represent pairing schemes of electrons in the atomic orbitals as shown in \(9\) through \(13\):

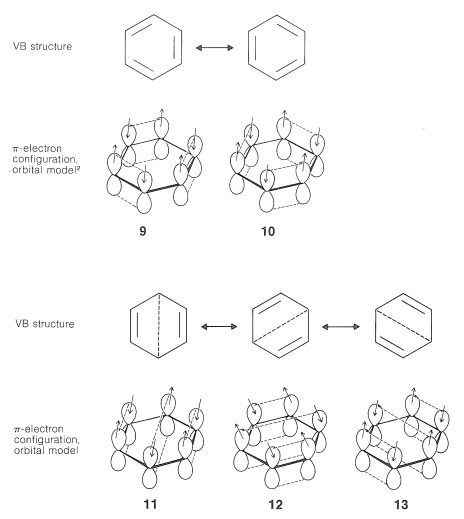
Pairing schemes \(9\) and \(10\) correspond to Kekule's structures, whereas \(11\), \(12\), and \(13\) are called "Dewar structures" because J. Dewar suggested, in 1869, that benzene might have a structure such as \(14\):

The electrons are paired in the configurations represented by \(11\), \(12\), and \(13\), but these pairing schemes are not as energetically favorable as \(9\) and \(10\). The reason is that the two electrons paired according to the dashed lines in \(11\), \(12\), and \(13\) are on nuclei separated by \(2.8\) Å, which is too far apart for effective bonding. The dashed lines between the distant carbons in \(11\), \(12\), and \(13\) are significant only in that they define a pairing scheme. Such lines sometimes are said to represent "formal bonds".

We hope that it is clear from what we have said here and previously that the electron-pairing schemes \(9\) through \(13\) do not separately have physical reality or independent existence; indeed, the energy of the actual molecule is less than any one of the contributing structures. The double-headed arrow between the structures is used to indicate that they represent different electron-pairing schemes for a molecule and not different forms of the molecule in equilibrium with one another. When we use the resonance method in a qualitative way, we consider that the contribution of each of the several structures is to be weighted in some way that accords with the degree of bonding each would have, if it were to represent an actual molecule with the specified geometry. Thus the Kekule-type electron-pairing schemes, \(9\) and \(10\), are to be taken as contributing equally and predominantly to the hybrid structure of benzene - equally because they are energetically equivalent, and predominantly because they can contribute much more to the overall bonding than \(11\), \(12\), and \(13\).

In using the resonance method, we assume that all the resonance structures contributing to a given resonance hybrid have exactly the same spatial arrangements of the nuclei but different pairing schemes for the electrons. Therefore \(11\), \(12\), and \(13\) are not to be confused with bicyclo[2.2.0]-2,5-hexadiene, \(15\), because \(15\) is a known (albeit not very stable) molecule with different atom positions and therefore vastly different bond angles and bond lengths from benzene:

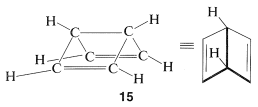
The electron-pairing schemes \(9\) and \(10\) represent the electron pairing that \(15\) would have if it were grossly distorted, with each carbon at the corner of a regular hexagon and a formal bond in place of a carbon-carbon single bond. Thus \(9\) and \(10\) would not contribute in a significant way to the resonance hybrid of \(15\).

Clearly, it is inconvenient and tedious to write the structures of the contributing forms to show the structure of a resonance hybrid. A shorthand notation is therefore desirable. Frequently, dashed rather than full lines are used where the bonding electrons are expected to be delocalized over several atoms. For benzene, \(16a\) or \(16b\) is quite appropriate:

Unfortunately, although these are clear and explicit renderings, they are tedious to draw. As a result, many authors use (as we will most often) a single Kekule structure to represent benzene, with the understanding that all the \(\ce{C-C}\) bonds are equivalent. Other authors choose to represent benzene as a hexagon with an inscribed circle:

This is a simple notation for benzene, but is quite uninformative and even can be actively misleading with some aromatic ring systems, and thus should be used with this limitation in mind.

In calculations of the resonance energy of benzene, the five electronic configurations (valence-bond structures \(9\) through \(13\)) are combined mathematically to give five hybrid states, and of these the lowest-energy state is assumed to correspond to the normal state of the molecule. Thus benzene is considered by this approach to be a resonance hybrid of the valence-bond structures \(9\) through \(13\). In this simple treatment, \(9\) and \(10\) are calculated to contribute about \(80\%\) and \(11\), \(12\), and \(13\) about \(20\%\) to the hybrid. The actual numerical VB calculations, which are much more difficult to carry through than the corresponding MO calculations, give an energy of \(Q + 2.61 J\) for benzene and \(Q + 1.50 J\) for classical 1,3,5-cyclohexatriene.\(^3\) The resonance or delocalization energy then is \(\left( Q + 2.61 J \right) - \left( Q + 1.50 J \right) = 1.11 J\), which makes \(J \sim 35 \: \text{kcal mol}^{-1}\) if the resonance energy is taken to be equal to the \(38 \: \text{kcal}\) value obtained for the stabilization energy. If one carries through a simple VB calculation of the relative energy change associated with attack of \(\ce{Br}^\oplus\) on benzene as compared to 1,3,5-cyclohexatriene, the value obtained is \(0.63 J\), which corresponds to \(22 \: \text{kcal}\). This is in excellent agreement with the \(19 \: \text{kcal}\) value obtained by the MO method (Section 21-3C).

\(^1\)There are many excellent books that cover this subject in great detail; however, the simplest introductory work is J. D. Roberts, Molecular Orbital Calculations, W. A. Benjamin, Inc., Menlo Park, Calif., 1961.

\(^2\) Note that in \(9\) and also in \(10\), we show a particular way of pairing the electrons. However, just as \(1 \leftrightarrow 2\), and \(4a \leftrightarrow 4b\), we also must consider other sets that represent exchanges of electrons across the dashed lines of \(9\) and also of \(10\).

\(^3\)\(Q\) and \(J\) are negative VB energy parameters that correspond roughly to the MO parameters \(\alpha\) and \(\beta\).

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."