21.3: Comparison of the Resonance and Molecular-Orbital Methods
- Page ID
- 22312
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Electron-Pair Bond
In this section, we will sketch the similarities and differences in the resonance (or valence-bond, VB) and molecular-orbital (MO) approaches for electron-pair bonds. Both methods normally start with atomic orbitals \(1s\), \(2s\), \(2p\), and so on, of the types discussed in Section 6-1. Where the methods differ is in how these orbitals are used. For a bond between two atoms, the MO procedure combines (or mixes) two atomic orbitals, one from each atom, with proper account of orbital phase (Section 6-2) to obtain two molecular orbitals, one of low energy and one of higher energy. The atomic orbitals can be pure or hybrid orbitals (Sections 6-1 and 6-4). In Figure 21-2, we show the results of combining the \(1s\) orbitals of hydrogen. The calculation for the most stable state proceeds by determining the energy of the system when two paired electrons are in the low-energy molecular orbital. The binding energy is the difference between the energy so calculated and the energies of the separated atoms. Because the molecular orbital extends over both atoms, the bonding electrons must be associated with both atoms.
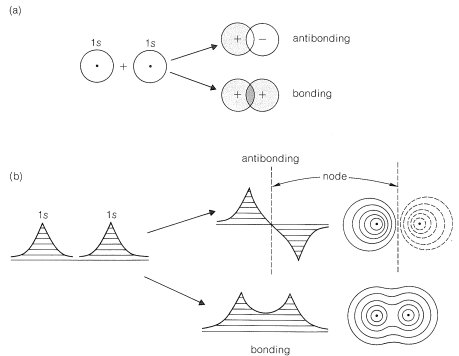
Remember, the MO method first combines the atomic orbitals to give molecular orbitals, then populates the molecular orbitals with electrons (no more than two paired electrons per orbital). This part of the procedure is similar to the way electrons are allocated to atomic orbitals (Section 6-1).
The VB treatment starts with the same atomic orbitals but assigns one electron to each orbital. For an electron-pair bond between two hydrogen atoms, the VB treatment in its simplest form considers two electronic configurations. One of these has electron 1 in the orbital of hydrogen 1 and electron 2 in the orbital of hydrogen 2, \(\left( 1 \right)\). The other configuration, \(2\), has electron 2 in the orbital of hydrogen 1 and electron 1 in the orbital of hydrogen 2:
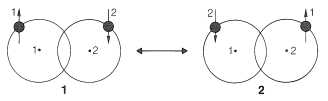
The calculation then proceeds to predict a low-energy state and a high-energy state. These states can be regarded as hybrids of \(1\) and \(2\). The low-energy state, which is the one of more interest to us, usually is called a resonance hybrid.
In the VB method, each of the electrons becomes associated with both atoms through the mixing of the two configurations. A very important point here is that the calculation that mixes \(1\) and \(2\) leads to a six times greater binding energy than calculated for \(1\) and \(2\) alone. Thus in the VB treatment we combine electronic configurations (here \(1\) and \(2\), \(\leftrightarrow\) symbolizing mixing), whereas in the MO treatment we combine atomic orbitals to get low- and high-energy molecular orbitals.
What is the Glue in These Bonds?
The forces that hold atoms together through chemical bonds are electrostatic, that is, the attraction of positively charged nuclei for negatively charged electrons. But the energy calculated for a single configuration, such as \(1\), only accounts for about one sixth of the total binding. In either the VB or the MO method the electrons in an electron pair between two nuclei brought to within bonding distances are equivalent and indistinguishable. That is, we are unable to identify one electron any more than the other with a given atom. The significance of the pairing of the electrons is that is permits each electron to have maximum possible freedom to move through the orbitals of the two-atom system rather than being "localized" on particular atoms. Quantum-mechanical calculations tell us that freedom of motion of the electrons is very important. Thus, using the VB method, we calculate that fully five sixths of the binding of the hydrogen molecule is associated with the "delocalization" of the electrons between the two nuclei.
There are many compounds with structures in which electrons are delocalized over more than two atoms. Such molecules should be more stable than would be expected for molecules with the same geometry but with electron pairs constrained to be associated with just one or two atoms. We will shortly discuss some specific examples, but because most of these examples involve the delocalization of \(\pi\) electrons, it is expedient to first discuss ethene as a prototype, using both the MO and VB methods.
The \(\pi\) Bond in Ethene
The atomic-orbital picture of ethene (Figure 6-14) formulates the \(\pi\) bond as resulting from overlap of two adjacent \(p\) atomic orbitals, one from each of two \(sp^2\) hybridized carbons. The \(p\) orbitals are directed perpendicularly to the plane defined by the hybrid orbitals of the \(\sigma\) bonds, and to a first approximation, we assume that exchange of the \(\pi\) and \(\sigma\) electrons between their respective orbitals does not affect the energy of the molecule. If this assumption is valid, \(\pi\) bonding can be treated independently of \(\sigma\) bonding. Although undoubtedly oversimplified, the VB and MO methods have been remarkably successful using this assumption. In our subsequent discussions, we shall treat the \(\pi\) electrons separately from localized \(\sigma\) electrons.
The \(\pi\) bond of the ethene molecule can be formulated very much like the bond in the hydrogen molecule (Section 21-2A), with the difference that the bonding is achieved by the overlap of two \(2p\) atomic orbitals of carbon rather than two \(1s\) atomic orbitals of hydrogen.
In the MO method the mixing of the two \(2p\) atomic orbitals gives two molecular orbitals. The details of the mathematics of the mixing process to give an optimum set of molecular orbitals are well beyond the scope of this book,\(^1\) but the results are shown in Figure 21-3. The two \(\pi\) electrons of ethene are taken as occupying the low-energy bonding orbital, while the high-energy antibonding orbital normally is empty.
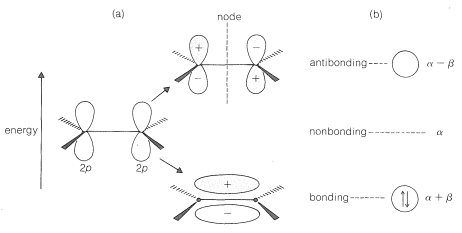
How much more stable is the bonding molecular orbital relative to a pair of noninteracting \(p\) atomic orbitals? It is difficult to provide a numerical answer in \(\text{kcal mol}^{-1}\) that is meaningful, but we can describe the energy in symbolic terms. First, the energy of one electron in the \(p\) atomic orbital of an \(sp^2\)-hybridized carbon, as in \(3\), is taken as a standard quantity, \(\alpha\), often called the Coulomb energy:
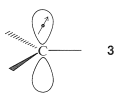
Thus, if there were no \(\pi\) bonding in ethene and no repulsion between the electrons, the energy of the two electrons (one in each of the two adjacent \(p\) orbitals of the carbons) would be twice the Coulomb energy, or \(2 \alpha\). This would be the situation for two carbons such as \(3\) that are widely separated.
The MO calculation shows that the bonding molecular orbital of ethene is more stable (of lower energy) than the nonbonding level, \(\alpha\), by a quantity, \(\beta\), where \(\beta\) is a negative energy term (Figure 21-3). Likewise, the antibonding level is destabilized by an amount \(-\beta\). For two paired electrons in the bonding molecular orbital, the \(\pi\)-electron energy of ethene is calculated to be \(2 \left( \alpha + \beta \right) = 2 \alpha + 2 \beta\).
In the valence-bond approach, the \(\pi\) bond of ethene is considered to be a hybrid of all reasonable electronic configurations of two indistinguishable paired electrons distributed between two \(p\) orbitals. Each of the configurations that can be written, \(4a\), \(4b\), \(4c\), and \(4d\), have identical locations of the atomic nuclei in space:
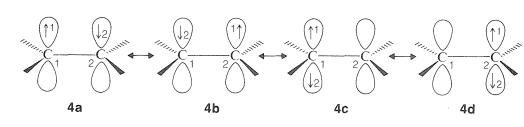
The four valence-bond structures or configurations, \(4a\)-\(d\), are combined mathematically to give four hybrid states, and of these, the lowest-energy one corresponds approximately to the normal state of the molecule. The calculation shows that the structures \(4a\) and \(4b\), which have one electron in each \(p\) orbital, are the major contributors to the "hybrid" of ethene. The valence-bond structures, \(4c\) and \(4d\), are ionic structures, which correspond to the conventional formulas, \(4e\) and \(4f\):

These valence-bond structures are not important to the \(\pi\) bond of the ground state of ethene, although they are important for carbonyl bonds (Section 16-1B).
\(^1\)There are many excellent books that cover this subject in great detail; however, the simplest introductory work is J. D. Roberts; Molecular Orbital Calculations, W. A. Benjamin, Inc., Menlo Park, Calif., 1961.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


