21.7: Which Is Better- MO or VB?
- Page ID
- 22316
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The calculated energy of the electron-pair bond of the hydrogen molecule as a function of \(\ce{H-H}\) intermolecular distance \(r\) by the ab initio (exact), MO, and VB procedures is shown in Figure 21-11. The results show that neither the MO nor the VB calculations come close to the ab initio calculation in reproducing the experimental dissociation energy, \(D_e\), or the variation of the energy with the intermolecular distance. The VB method gives a little better energy value at the minimum and the MO method gives poor results at larger values of \(r\). We can say that, as calculated by the MO method, the molecule does not "dissociate properly".
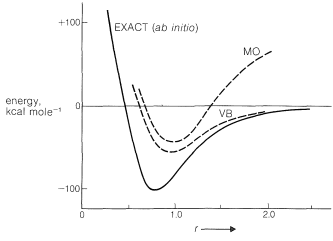
Within the calculations of the MO method, the molecule does not "dissociate properly".
Why do these calculations yield results so far from the ab initio curve? There are two reasons. First, atomic orbitals are used that are appropriate for isolated atoms, but are hardly expected to be the best orbitals for the electrons when two or more atoms are in close proximity. It is convenient to use atomic orbitals in simple calculations because they are mathematically simple, but more complicated orbitals are known to give better results. Second, neither treatment properly takes into account electron-electron repulsions. For two electrons, a term of the form \(\frac{e^2}{r^2_{12}}\) (in which \(e\) is the electronic charge and \(r_{12}\) is the distance between the electrons) is required to describe the repulsion between electrons. The exact calculations avoid both difficulties but are so complex mathematically as to be devoid of any capability for providing qualitative understanding.
The VB method gives a slightly lower energy than the MO method at the minimum, because in the simple MO method, when we calculate the energy resulting from two electrons going into the lowest molecular orbital, we put no restraints on their being close together. As a result there is a \(50\%\) probability for both electrons being simultaneously in either half of the molecular orbital. In contrast, the simple VB method combines configurations \(1\) and \(2\), each having just one electron per atomic orbital, and no account is taken of the possibility of either atomic orbital containing more than one electron. This is equivalent to neglecting the pairing schemes \(\ce{H}^\ominus \ce{H}^\oplus \leftrightarrow \ce{H}^\oplus \ce{H}^\ominus\). Neither the VB nor the MO approximation is the best possible; the simple MO method tends to take too little account of interelectronic repulsion, whereas the VB method tends to take too much account of it. However, as can be seen in Figure 21-11, taking too much account of electron repulsion is the better approximation.
Why does an electron-pair bond calculated by the MO method not dissociate properly? We have seen that half of the time both electrons in the low-energy molecular orbital are in the vicinity of just one of the nuclei. But as the nuclei move far apart, this corresponds to a far greater energy than having only one electron in the vicinity of each nucleus, as the VB method suggests.
There is no unequivocal answer to the question as to which is the better method. Calculations by the VB method are likely to be more reliable than those by the MO method, but in practice are much more difficult to carry out. For many-electron molecules the MO procedure is simpler to visualize because we combine atomic orbitals into molecular orbitals and then populate the lower-energy orbitals with electrons. In the VB method, atomic orbitals are occupied, but the electrons of different atoms are paired to form bonds, a process that requires explicit consideration of many-electron wave functions. To put it another way, it is easier to visualize a system of molecular orbitals containing \(N\) electrons than it is to visualize a hybrid wave function of \(N\) electrons.
How can the MO and VB methods be improved? The answer depends on what one wants - more accurate calculations or better qualitative understanding. To improve VB calculations we need orbitals that allow the electrons to spread out over more than one atom. The GVB orbitals discussed in Section 6-6 suit this purpose and give an energy curve only slightly above the exact curve of Figure 21-11. In the GVB treatment the orbitals delocalize less as \(r\) increases.
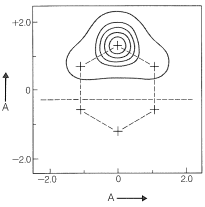
When atomic orbitals are derived for each carbon of the \(\pi\)-electron system of benzene by the GVB method, they are somewhat more spread out than simple carbon \(p\) orbitals (Figure 21-12). Use of these orbitals in VB calculations gives excellent results with just the two pairing schemes of benzene, \(9\) and \(10\).
Improvement of the MO method involves better orbitals, better account of interelectronic repulsion, and introduction of mixing of different electron configurations in the molecular orbitals ("configuration interaction"). Improved MO calculations give much more accurate energies at the minimum of a plot such as Figure 21-11, but the bonds still do not dissociate properly, for the same reason as with the simple MO method.
We cannot say that either the VB or the MO method is more correct; only that one approximation may be more useful than the other in attempting to solve a particular problem. The fact is, the more each is refined, the more they appear to merge into a common procedure; but, unfortunately, in the refinement process the mathematics become so complex that qualitative understanding of what is being done tends to disappear altogether.
We cannot say that either the VB or the MO method is more correct; only that one approximation may be more useful than the other in attempting to solve a particular problem.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


