6.6: The pH
- Page ID
- 371807
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)What is pH?
The acidity of an aqueous solution relates to H3O+ ion concentration, but there are two problems with it. The first problem is that the molar concentration of hydronium ion [H3O+] varies over a wide range, usually from 1-to-0.00000000000001 which is not easy to comprehend. Log scale solves the problem, e.g., if a number increases from 1 to 1000, it increases from 0 to 3 on a log scale to the base 10. The second problem is that the [H3O+] is usually a small number between 0 and 1. The log of a number that is between 0 and 1 is a negative number that is not easy to grasp mentally. If a number is between 0 and 1, its reciprocal is more than 1, and its log is a +ve number.
The pH is defined as a log of reciprocal of the molar concentration of hydronium ions [H3O+]. It can also be stated that the pH is a negative log of the molar concentration of hydronium ion [H3O+]. The mathematical form of the pH is the following.
\begin{equation}
p H=\log \frac{1}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\nonumber
\end{equation}
A pH is usually a positive number between 0 to 14.
Calculating pH
First, determine the molar concentration of hydronium ion [H3O+]. Than take log base 10 of [H3O+] and change the sign of the answer, i.e.:
\begin{equation}
p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\nonumber
\end{equation}
Calculate the pH of neutral water that has [H3O+] = 10-7M?
Solution
Given [H3O+] = 10-7 M, desired pH = ?
Formula: \(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\)
Plug in values and calculate: \(p H=-\log \left(10^{-7}\right)=7.0\)
The keys-sequence for the calculation on a Microsoft Window’s scientific calculator is (the last box is the output of the keys-sequence):

The given number in scientific notation is 1 x 10-7 which has one significant figure shown by the coefficient part of the number in bold font. The number of decimal places in the pH number shows the significant figures, i.e., 7.0 has one decimal place shown in bold font, which means it has one significant figure.
Calculate the pH of the 0.010 M HCl solution?
Solution
Given [HCl] = 0.010 M = [H3O+], desired pH = ?
Formula: \(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\)
Plug in values and calculate: \(p H=-\log (0.010)=2.00\)
The keys-sequence for the calculation on a Microsoft Window’s scientific calculator is (the last box is the output of the keys-sequence):

Note that the given number 0.010 M has two significant figures shown in bold fonts. So, the answer pH 2.00 also has two significant figures shown in bold fonts.
Calculate the pH of 0.10 M HCl solution?
Solution
Given [HCl] = 0.10 M = [H3O+], desired pH = ?
Formula: \(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\)
Calculations: \(p H=-\log (0.10)=1.00\)
As the acid 0.01M and 0.10M is gradually added to increase the acid from neutral water in example 1 to 0.01M in example 2 to 0.10 M in example 3, , the pH gradually decreased from 7 to 2 to 1.
The pH of the acidic solution is less than 7. The more acidic the solution, the lower the pH.
The pH decreases as the [H3O+] increases because the reciprocal of [H3O+] is used in the pH calculation. The larger the given number, the smaller the reciprocal; it translates to “the more acidic the solution, the lower the pH.
Calculate the pH of 0.010 M NaOH solution?
Solution
Given [NaOH] = 0.010 M = [OH-], desired pH = ?
First, calculate [H3O+] from the give [OH-]: \(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=10^{-14} /\left[\mathrm{OH}^{-}\right]=10^{-14} / 0.010=1.0 \times 10^{-12}\)
Than calculate the pH: \(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=-\log \left(1.0 \times 10^{-12}\right)=12.00\)
Note that the given number 0.010 M has two significant figures shown in bold fonts. So, the answer pH 12.00 also has two significant figures shown in bold fonts.
Calculate the pH of 0.10 M NaOH solution?
Solution
Given [NaOH] = 0.10 M = [OH-], desired pH = ?
First, calculate [H3O+] from the give [OH-]: \(10^{-14} /\left[\mathrm{OH}^{-}\right]=10^{-14} / 0.10=1.0 \times 10^{-13}\)
Formula: [H3O+] = 10-14/[OH-] = 10-14/0.10 = 1.0 x 10-13.
Than calculate the pH: \(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=-\log \left(1.0 \times 10^{-13}\right)=13.00\)
As the base, 0.010M and 0.10M are gradually added in the previous two exams to the neutral water at pH 7, the pH increases from 7 to 12 to 13.
The pH of the basic solution is more than 7. The more basic the solution, the higher the pH.
pH measurement
The pH is usually measured in laboratories by digital pH meters. The electrode of the pH meter is first calibrated with solutions of know pH values, and then the electrode is dipped in the test solution to read its pH value. Universal pH indicator papers are available that turn to a specific color when placed in the solution. The pH is read by matching the color of the test paper with the color on the chart. Fig. 6.6.1 shows a digital pH meter and two universal pH indicating papers commonly used for pH measurements in laboratories.



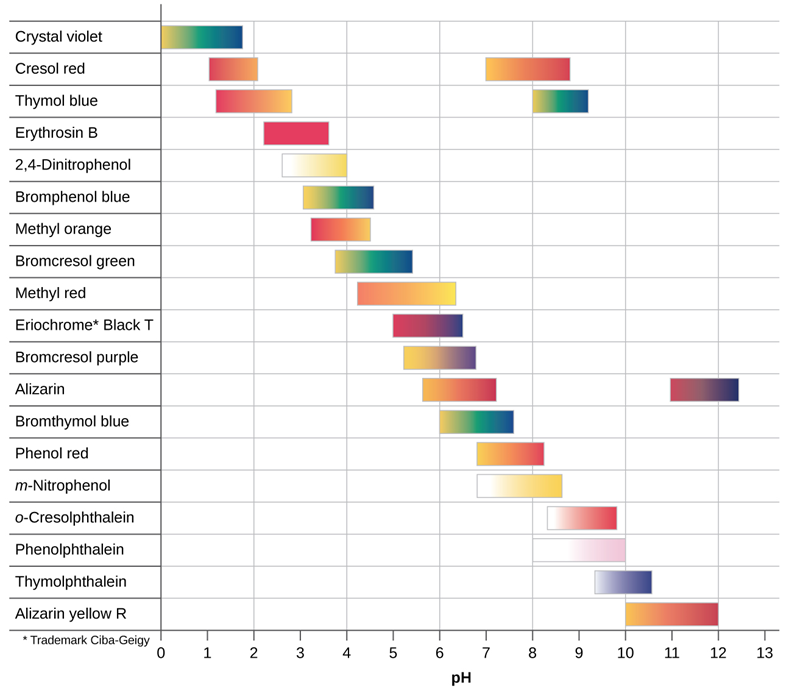
The pH indicators are weak acids or weak bases that change color in a specific pH range. A few drops of the solution of a pH indicator paper are added to the test solution in which pH is changed by adding acid or base. The change in the color of the solution indicates the pH range in which the indicator changes the color. Figure 6.6.2 shows the colors and the color transition ranges of some of the common pH indicators.
Calculating hydronium ion concentration from pH
The formula for calculating the molar concentration of hydronium ions [H3O+] is obtained by rearranging the pH formula. \(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\), re-arranges to: \(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\operatorname{antilog}(-p H)=10^{-p H}\).
Calculate [H3O+] of a urine sample that has pH 7.56?
Solution
Given: pH = 7.56, Desired: [H3O+] = ?
Formula: \(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=10^{-p H}\).
Plug in the values and calculate: \(\left[H_{3} O^{+}\right]=10^{-p H}=10^{-(7.56)}=2.8 \times 10^{-8} M\)
The keys-sequence for the calculation on a Microsoft Window’s scientific calculator is (the last box is the output of the keys-sequence):

The calculated answer in the above example is a lengthy number, but it is rounded to two significant figures shown in bold font in 2.8\(\times 10^{-8} M\), because the given number pH 7.56 has two significant figures shown in bold font.
Significance of pH Scale
The pH scale varies from ~0 to ~14. The pH of 7 is neutral, pH more than 7 is basic, and pH less than 7 is acidic, as illustrated in Fig. 6.6.3. Different foods have different pH values, as shown in Fig. 6.1.1. Similarly, several of the acids and bases in household use have a specific pH range, as shown in Fig. 6.6.3.
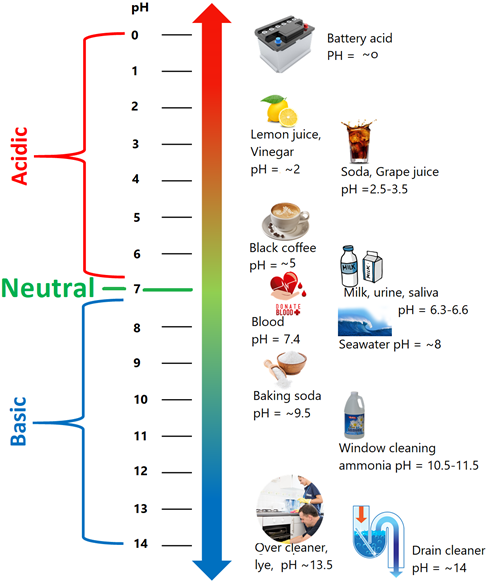
The control of pH is essential in the proper functioning of biological systems. Plants thrive if the soil does not have too acidic or too basic a pH. Lacks and revers have a specific range of pH in which the aquatic life can survive. US natural water has a pH in the range of 6.5 to 8.5 range. Seawater has a specific narrow range of pH 7.5 to pH 8.4 in which the life in the sea can function correctly.
The pH of body fluids
Human body fluids vary in pH, as shown in Fig. 6.6.4. Saliva in the mouth is slightly acidic, but the stomach has the lowest pH in the body. The strongly acidic pH in the stomach helps in digesting some foods, and it also helps in killing bacteria that may enter the stomach through the foods. When the food enters the large intestine, the pH changes to basic which helps in digesting the foods that could not be digested in the acidic environment of the stomach. The pH changes to more basic in the small intestine.
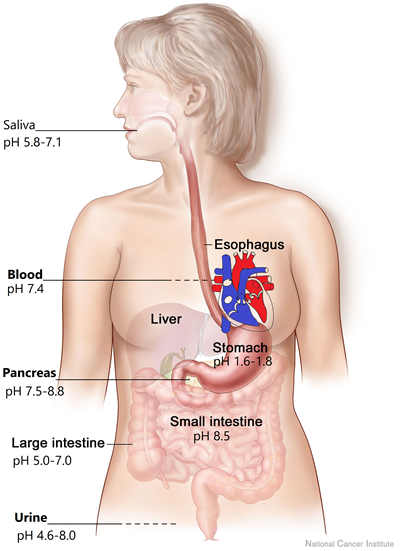
The blood has a pH of 7.4, and it can vary in a small range of 7.35 to 7.45. If the blood pH goes outside of the 7.35 to 7.45 range it can result in medical problems. Enzymes in the body need a specific pH range because hydrogen bonding plays a vital role in the structures needed for proper functioning. pH changes affect the hydrogen bonding and can make the enzymes less active or may inactivate them. The pH of blood is maintained by a complex action of buffers that are described in the later sections. The pH of urine can vary over a broad range from 4.6 to 8, depending on the recent diet and exercises.
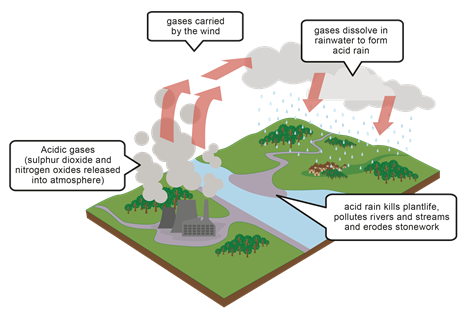
Acid rain
Acidic gases like NO, NO2, N2O4, SO2 are released into the environment primarily during the combustion of fossil fuels. These gases dissolve in the rainwater and make the rain acidic. For example, sulfur dioxide dissolves in water and makes sulfurous acid:
\[\mathrm{SO}_{2}(\mathrm{~g})+\mathrm{H}_{2} \mathrm{O}(\mathrm{I}) \rightleftarrows \mathrm{H}_{2} \mathrm{SO}_{3}(\mathrm{aq})\nonumber\]
The acid rain damages the environment by making the soil, river water, and lack-water acidic. The acidic soil and water, in turn, affect the plants and aquatic life. The acid water also reacts with calcium carbonate and corrodes metals that are responsible for damage to the sculpture and other structures, as illustrated in Fig. 6.6.5, Fig. 6.6.6, and Fig. 6.6.7.