6.5: Dissociation of water

How do water molecules dissociate?

Water is an amphoteric substance, which means water can accept a proton acting as a base, and it can also donate A proton acting as an acid.

About one water molecule in half a billion dissociates into an OH^- ion by losing a proton to another water molecule. The molecule that receives a proton becomes H₃O⁺.

The dissociation of water is an equilibrium reaction in which one water molecule donates its proton to another water molecule.

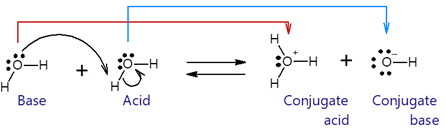
The water molecule that receives proton is acting as a base, and it converts to conjugate acid H₃O⁺. The other water molecule that donates a proton is acting as an acid, and it converts to conjugate base OH^-. The arrows in the reaction show that the base uses one of its lone pairs of electrons to make a bond with proton, and the previous bond pair of electrons turns into a third lone pair of electrons on the oxygen atom of the base. The reaction is reversible, i.e., the conjugate acid (H₃O⁺) and the conjugate base (OH^-) react to re-form the two water molecules.

Water dissociation constant

The dissociation of water is an equilibrium reaction. It means the rate of the forward reaction is equal to the rate of the reverse reaction and the concentration of the reactants and products do not change at equilibrium. The molar concentration of H₃O⁺ represented as [H₃O⁺] is equal to 10^-7 M in a pure water sample at 25 ^oC, where M is in moles/Liter. The molar concentration of OH^- represented as [OH^-] is equal to the molar concentration of H₃O⁺ in pure water, i.e., [H₃O⁺] = [OH^-] = 10^-7 M.

The product of the molar concentration of H₃O⁺ and OH^- in water is a constant called water dissociation constant K_w equal to 10^-14 at 25 ^oC, i.e.:

\[\mathrm{K}_{\mathrm{w}}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=\left(10^{-7}\right)\left(10^{-7}\right)=10^{-14}\nonumber\nonumber\]

Neutral, acidic, or basic aqueous solutions

A solution that has an equal concentration of H₃O⁺ and OH^-, each equal to 10^-7 M, is a neutral solution.

An acidic solution has an acid dissolved in water. When an acid dissolves in water it dissociates adding more H₃O^+. The [OH^-] must decrease to keep the K_w constant.

A solution that has [H₃O⁺] more than 10^-7, and [OH^-] less than 10^-7 is an acidic solution.

A basic solution has a base dissolved in water. When a base dissolves in water it dissociates adding more OH^-. The [H₃O⁺] must decrease to keep the K_w constant.

A solution that has [H₃O⁺] less than 10^-7, and [OH^-] more than 10^-7 is a basic solution.

Calculations of [H₃O⁺] and [OH^-] based on K_w

The water dissociation constant remains the same whether the aqueous solution is neutral, acidic, or basic, i.e.:

\begin{equation}
\mathrm{K}_{\mathrm{w}}=\left[\mathrm{H}_{3} \mathrm{O}_{-}^{+}\right]\left[\mathrm{OH}^{-}\right]=\left(10^{-7}\right)\left(10^{-7}\right)=10^{-14} \text { at } 25^{\circ} \mathrm{C}\nonumber
\end{equation}

Therefore, if the molar concentration of hydronium ions [H₃O⁺] is known, the molar concentration of hydroxide ions [OH^-] can be calculated using the following formula:

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{\mathrm{K}_{w}}{[\mathrm{OH}^{-}]}=\frac{10^{-14}}{[\mathrm{OH}^{-}]}\nonumber\]

Similarly, if the molar concentration of hydroxide ions [OH^-] is known, the molar concentration of hydronium ions [OH^-] can be calculated using the following formula:

\[\left[\mathrm{OH}^{-}\right]=\frac{K_{w}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{10^{-14}}{\left[\mathrm{H}_{3}\mathrm{O}^{+}\right]}\nonumber\]

When a strong acid like HCl dissolves in water, it dissociates ~100% into ions. Therefore, the [H₃O⁺] is equal to the molar concentration of the acid. The amount H₃O⁺ added by dissociation of water molecules is very small compared to that coming from the dissociation of a strong acid and can be neglected. Similarly, when a strong base like NaOH dissolves in water, it dissociates ~100% into ions. Therefore, the [OH^-] is equal to the molar concentration of the base.

Note

When a weak acid or a weak base dissolves in water, it partially dissociates into ions. Therefore, the [H₃O⁺] or the [OH^-] in the cases of weak acids and weak bases has to be determined experimentally for the calculations.

Example \(\PageIndex{1}\)

Calculate the concentration of OH^- ions in a 0.10 M HNO₃ solution?

Solution

The HNO₃ is a strong acid. Therefore, [HNO₃] = 0.10 M = [H₃O⁺]. Desired [OH^-] = ?

Formula: \(\left[\mathrm{OH}^{-}\right]=\frac{10^{-14}}{\left[\mathrm{H}_{3}\mathrm{O}^{+}\right]}\)

Plug in values an calculate: \(\left[0 \mathrm{H}^{-}\right]=\frac{10^{-14}}{0.10}=10^{-13}\mathrm{~M}\)

Example \(\PageIndex{2}\)

A vinegar solution has [H₃O⁺] = 2.0 x 10^-3. a) What is the hydroxide ion concentration in the vinegar solution? b) is the solution acidic, basic, or neutral?

Solution

a) Given [H₃O⁺] = 2.0 x 10^-3. Desired [OH^-] = ?

Formula: \(\left[\mathrm{OH}^{-}\right]=\frac{10^{-14}}{\left[\mathrm{H}_{3}\mathrm{O}^{+}\right]}\)

Plug in values and calculate: \(\left[0 H^{-}\right]=\frac{10^{-14}}{2.0 \times 10^{-3}}=5.0 \times 10^{-12} \mathrm{M}\)

b) The solution is acidic because [H₃O⁺] > [OH^-].

Example \(\PageIndex{3}\)

Calculate the value of [H³O⁺] and [OH^-] in a 0.010 M NaOH solution?

Solution

The NaOH is a strong base. Therefore [NaOH] = 0.010 M = [OH^-]. Desired [H₃O⁺] = ?

Formula: \(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\mathrm{K}_{\mathrm{w}} /\left[\mathrm{OH}^{-}\right]=10^{-14} /\left[\mathrm{OH}^{-}\right]\)

Calculations: \(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=10^{-14} / 0.010=10^{-12} \mathrm{M}\)

Example \(\PageIndex{4}\)

a) Calculate the [H₃O⁺] in an ammonia solution that has [OH^-] = 4.0 x 10^-4 M? b) Is the

solution acidic, basic, or neutral?

Solution

a) Given [OH^-] = 4.0 x 10^-4. Desired [H₃O⁺] = ?

Formula:\(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\mathrm{K}_{\mathrm{w}} /\left[\mathrm{OH}^{-}\right]=10^{-14} /\left[\mathrm{OH}^{-}\right]\)

Calculations: \(\left[0 H^{-}\right]=\frac{10^{-14}}{4.0 \times 10^{-4}}=2.5 \times 10^{-11} \mathrm{M}\)

b) The solution is basic because [H₃O⁺] < [OH^-].