Precipitation Reactions
- Page ID
- 727
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Precipitation reactions occur when cations and anions in aqueous solution combine to form an insoluble ionic solid called a precipitate. Whether or not such a reaction occurs can be determined by using the solubility rules for common ionic solids. Because not all aqueous reactions form precipitates, one must consult the solubility rules before determining the state of the products and writing a net ionic equation. The ability to predict these reactions allows scientists to determine which ions are present in a solution, and allows industries to form chemicals by extracting components from these reactions.
Properties of Precipitates
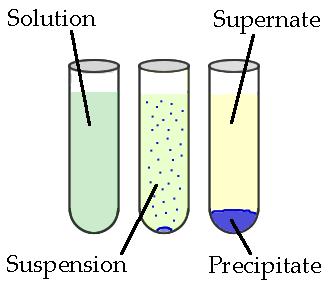
Precipitates are insoluble ionic solid products of a reaction, formed when certain cations and anions combine in an aqueous solution. The determining factors of the formation of a precipitate can vary. Some reactions depend on temperature, such as solutions used for buffers, whereas others are dependent only on solution concentration. The solids produced in precipitate reactions are crystalline solids, and can be suspended throughout the liquid or fall to the bottom of the solution. The remaining fluid is called supernatant liquid. The two components of the mixture (precipitate and supernate) can be separated by various methods, such as filtration, centrifuging, or decanting.
Precipitation and Double Replacement Reactions
The use of solubility rules require an understanding of the way that ions react. Most precipitation reactions are single replacement reactions or double replacement reactions. A double replacement reaction occurs when two ionic reactants dissociate and bond with the respective anion or cation from the other reactant. The ions replace each other based on their charges as either a cation or an anion. This can be thought of as "switching partners"; that is, the two reactants each "lose" their partner and form a bond with a different partner:

A double replacement reaction is specifically classified as a precipitation reaction when the chemical equation in question occurs in aqueous solution and one of the of the products formed is insoluble. An example of a precipitation reaction is given below:
\[\ce{CdSO4(aq) + K2S(aq) \rightarrow CdS(s) + K2SO4(aq)} \nonumber \]
Both reactants are aqueous and one product is solid. Because the reactants are ionic and aqueous, they dissociate and are therefore soluble. However, there are six solubility guidelines used to predict which molecules are insoluble in water. These molecules form a solid precipitate in solution.
Whether or not a reaction forms a precipitate is dictated by the solubility rules. These rules provide guidelines that tell which ions form solids and which remain in their ionic form in aqueous solution. The rules are to be followed from the top down, meaning that if something is insoluble (or soluble) due to rule 1, it has precedence over a higher-numbered rule.
- Salts formed with group 1 cations and \(\ce{NH4^{+}}\) cations are soluble. There are some exceptions for certain \(\ce{Li^{+}}\) salts.
- Acetates (\(\ce{C2H3O2^{-}}\)), nitrates (\(\ce{NO3^{-}}\)), and perchlorates (\(\ce{ClO4^{-}}\)) are soluble.
- Bromides, chlorides, and iodides are soluble.
- Sulfates (\(\ce{SO4^{2-}}\)) are soluble with the exception of sulfates formed with \(\ce{Ca^{2+}}\), \(\ce{Sr^{2+}}\), \(\ce{Pb^{2+}}\), and \(\ce{Ba^{2+}}\).
- Salts containing silver, lead, and mercury (I) are insoluble.
- Carbonates (\(\ce{CO3^{2-}}\)), phosphates (\(\ce{PO4^{3-}}\)), sulfides, oxides, and hydroxides (\(\ce{OH^{-}}\)) are insoluble. Sulfides formed with group 2 cations and hydroxides formed with calcium, strontium, and barium are exceptions.
If the rules state that an ion is soluble, then it remains in its aqueous ion form. If an ion is insoluble based on the solubility rules, then it forms a solid with an ion from the other reactant. If all the ions in a reaction are shown to be soluble, then no precipitation reaction occurs.
Net Ionic Equations
To understand the definition of a net ionic equation, recall the equation for the double replacement reaction. Because this particular reaction is a precipitation reaction, states of matter can be assigned to each variable pair:
AB(aq) + CD(aq) → AD(aq) + CB(s)
The first step to writing a net ionic equation is to separate the soluble (aqueous) reactants and products into their respective cations and anions. Precipitates do not dissociate in water, so the solid should not be separated. The resulting equation looks like that below:
A+(aq) + B-(aq) + C+(aq) + D-(aq) → A+(aq) + D-(aq) + CB(s)
In the equation above, A+and D- ions are present on both sides of the equation. These are called spectator ions because they remain unchanged throughout the reaction. Since they go through the equation unchanged, they can be eliminated to show the net ionic equation:
C+ (aq)+ B- (aq) → CB (s)
The net ionic equation only shows the precipitation reaction. A net ionic equation must be balanced on both sides not only in terms of atoms of elements, but also in terms of electric charge. Precipitation reactions are usually represented solely by net ionic equations. If all products are aqueous, a net ionic equation cannot be written because all ions are canceled out as spectator ions. Therefore, no precipitation reaction occurs.
Applications and Examples
Precipitation reactions are useful in determining whether a certain element is present in a solution. If a precipitate is formed when a chemical reacts with lead, for example, the presence of lead in water sources could be tested by adding the chemical and monitoring for precipitate formation. In addition, precipitation reactions can be used to extract elements, such as magnesium from seawater. Precipitation reactions even occur in the human body between antibodies and antigens; however, the environment in which this occurs is still being studied.
Complete the double replacement reaction and then reduce it to the net ionic equation.
\[\ce{NaOH(aq) + MgCl2(aq)} \rightarrow \nonumber \]
First, predict the products of this reaction using knowledge of double replacement reactions (remember the cations and anions “switch partners”).
\[\ce{2NaOH(aq) + MgCl2(aq) \rightarrow 2NaCl + Mg(OH)2} \nonumber \]
Second, consult the solubility rules to determine if the products are soluble. Group 1 cations (\(\ce{Na^{+}}\)) and chlorides are soluble from rules 1 and 3 respectively, so \(\ce{NaCl}\) will be soluble in water. However, rule 6 states that hydroxides are insoluble, and thus \(\ce{Mg(OH)2}\) will form a precipitate. The resulting equation is the following:
\[\ce{2NaOH(aq) + MgCl2(aq) \rightarrow 2NaCl(aq) + Mg(OH)2(s)} \nonumber \]
Third, separate the reactants into their ionic forms, as they would exist in an aqueous solution. Be sure to balance both the electrical charge and the number of atoms:
\[\ce{2Na^{+}(aq) + 2OH^{-}(aq) + Mg^{2+}(aq) + 2Cl^{-}(aq) \rightarrow Mg(OH)2(s) + 2Na^{+}(aq) + 2Cl^{-}(aq)} \nonumber \]
Lastly, eliminate the spectator ions (the ions that occur on both sides of the equation unchanged). In this case, they are the sodium and chlorine ions. The final net ionic equation is:
\[\ce{Mg^{2+}(aq) + 2OH^{-}(aq) \rightarrow Mg(OH)2(s)} \nonumber \]
Complete the double replacement reaction and then reduce it to the net ionic equation.
\[\ce{CoCl2(aq) + Na2SO4(aq)} \rightarrow \nonumber \]
Solution
The predicted products of this reaction are \(\ce{CoSO4}\) and \(\ce{NaCl}\). From the solubility rules, \(\ce{CoSO4}\) is soluble because rule 4 states that sulfates (\(\ce{SO4^{2-}}\)) are soluble. Similarly, we find that \(\ce{NaCl}\) is soluble based on rules 1 and 3. After balancing, the resulting equation is as follows:
\[\ce{CoCl2(aq) + Na2SO4(aq) \rightarrow CoSO4(aq) + 2 NaCl(aq)} \nonumber \]
Separate the species into their ionic forms, as they would exist in an aqueous solution. Balance the charge and the atoms. Cancel out all spectator ions (those that appear as ions on both sides of the equation.):
\[\cancel{\ce{Co^{2-}(aq)}} + \cancel{\ce{2Cl^{-}(aq)}} + \cancel{\ce{2Na^{+}(aq)}} + \cancel{\ce{SO4^{2-}(aq)}} \rightarrow \cancel{\ce{Co^{2-}(aq)}} + \cancel{\ce{SO4^{2-}(aq)}} + \cancel{\ce{2Na^{+}(aq)}} + \cancel{\ce{2Cl^{-}(aq)}} \nonumber\]
No precipitation reaction
This particular example is important because all of the reactants and the products are aqueous, meaning they cancel out of the net ionic equation. There is no solid precipitate formed; therefore, no precipitation reaction occurs.
Write the net ionic equation for this potentially double displacement reaction. Make sure to include the states of matter and balance the equations.
\[\ce{Fe(NO3)3(aq) + NaOH(aq)} \rightarrow\nonumber \]
- Answer
-
Regardless of physical state, the products of this reaction are \(\ce{Fe(OH)3}\) and \(\ce{NaNO3}\). The solubility rules predict that \(\ce{NaNO3}\) is soluble because all nitrates are soluble (rule 2). However, \(\ce{Fe(OH)3}\) is insoluble, because hydroxides are insoluble (rule 6) and \(\ce{Fe}\) is not one of the cations which results in an exception. After dissociation, the ionic equation is as follows:
\[\ce{Fe^{3+}(aq) + NO^{-}3(aq) + Na^{+}(aq) + 3OH^{-}(aq) \rightarrow Fe(OH)3(s) + Na^{+}(aq) + NO^{-}3(aq)} \nonumber \]
Canceling out spectator ions
\[\ce{Fe^{3+}(aq) + \bcancel{NO^{-}3(aq)} + \cancel{Na^{+}(aq)} + 3OH^{-}(aq) \rightarrow Fe(OH)3(s) + \cancel{Na^{+}(aq)} + \bcancel{NO^{-}3(aq)}} \nonumber \]
leaves the net ionic equation:
\[\ce{Fe^{3+}(aq) + 3OH^{-}(aq) \rightarrow Fe(OH)3(s)} \nonumber \]
Write the net ionic equation for this potentially double displacement reaction. Make sure to include the states of matter and balance the equations.
\[\ce{Al2(SO4)3(aq) + BaCl2(aq)} \rightarrow \nonumber \]
- Answer
-
From the double replacement reaction, the products are \(\ce{AlCl3}\) and \(\ce{BaSO4}\). \(\ce{AlCl3}\) is soluble because it contains a chloride (rule 3); however, \(\ce{BaSO4}\) is insoluble: it contains a sulfate, but the \(\ce{Ba^{2+}}\) ion causes it to be insoluble because it is one of the cations that causes an exception to rule 4. The ionic equation is (after balancing):
\[\ce{2Al^{3+}(aq) + 6Cl^{-}(aq) + 3Ba^{2+}(aq) + 3SO^{2-}4(aq) \rightarrow 2 Al^{3+}(aq) + 6Cl^{-}(aq) + 3BaSO4(s)} \nonumber \]
Canceling out spectator ions leaves the following net ionic equation:
\[\ce{Ba^{2+}(aq) + SO^{2-}4(aq) \rightarrow BaSO4(s)} \nonumber \]
Write the net ionic equation for this potentially double displacement reaction. Make sure to include the states of matter and balance the equations.
\[\ce{HI(aq) + Zn(NO3)2(aq)} \rightarrow \nonumber \]
- Answer
-
From the double replacement reaction, the products \(\ce{HNO3}\) and \(\ce{ZnI2}\) are formed. Looking at the solubility rules, \(\ce{HNO3}\) is soluble because it contains nitrate (rule 2), and \(\ce{ZnI2}\) is soluble because iodides are soluble (rule 3). This means that both the products are aqueous (i.e. dissociate in water), and thus no precipitation reaction occurs.
Write the net ionic equation for this potentially double displacement reaction. Make sure to include the states of matter and balance the equations.
\[\ce{CaCl2(aq) + Na3PO4(aq)} \rightarrow \nonumber \]
- Answer
-
The products of this double replacement reaction are \(\ce{Ca3(PO4)2}\) and \(\ce{NaCl}\). Rule 1 states that \(\ce{NaCl}\) is soluble, and according to solubility rule 6, \(\ce{Ca3(PO4)2}\) is insoluble. The ionic equation is:
\[\ce{Ca^{2+}(aq) + Cl^{-}(aq) + Na^{+}(aq) + PO^{3-}4(aq) \rightarrow Ca3(PO4)2(s) + Na^{+}(aq) + Cl^{-}(aq)} \nonumber \]
After canceling out spectator ions, the net ionic equation is given below:
\[\ce{Ca^{2+}(aq) + PO^{3-}4(aq) \rightarrow Ca3(PO4)2(s)} \nonumber \]
Write the net ionic equation for this potentially double displacement reaction. Make sure to include the states of matter and balance the equations.
\[\ce{Pb(NO3)2(aq) + K2SO4(aq)} \rightarrow \nonumber \]
- Answer
-
The first product of this reaction, \(\ce{PbSO_4}\), is insoluble according to rule 4 because it is a sulfate. The second product, \(\ce{KNO_3}\), is soluble because it contains nitrate (rule 2). Therefore, \(\ce{PbSO3(s)}\) will precipitate.
\[\ce{Pb^{2+}(aq) + SO4(aq) -> Pb(SO3)2(s)} \nonumber \]
References
- Campbell, Dan, Linus Pauling, and Davis Pressman. "The Nature of the Forces Between Antigen and Antibody and of the Precipitation Reaction." Physiological Reviews 23.3 (1943): 203-219. Online.
- Harwood, William, F Herring, Jeffry Madura, and Ralph Petrucci. General Chemistry. 9th ed. Upper Saddle River: Pearson Pretence Hall, 2007. Print.
- Freeouf, J.L, Grischkowsky, D., McInturff, D.T., Warren, A.C., & Woodall, J.M. (1990). Arsenic precipitates and the semi-insulating properties of gaas buffer layers grown by low-temperature molecular beam epitaxy. Applied Physics Letters, 57(13)
- Petrucci, et al. General Chemistry: Principles & Modern Applications. 9th ed. Upper Saddle River, New Jersey 2007.

