1.14: Stretching Frequencies and Structure Determination
- Page ID
- 204715
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Stretching Modes of Vibration
Often, we are only concerned with the stretching modes of vibrations for certain groups in a molecule. In this case, we can use the bonds to describe the stretching vibration for that group, though we have to consider all the bonds of the same type together. The general strategy is to come up with a reducible representation for only the bond vectors of the groups we are concerned with, then reduce them into their irreducible representations.
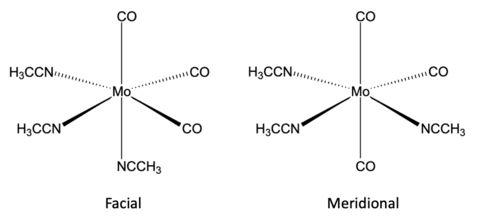
Consider the compound fac-Mo(CO)3(NCCH3)3 shown in Figure \(\PageIndex{1}\). We first determine the point group of the molecule, which is C3v for this molecule (character table shown in Table \(PageIndex{1}\)). We then use the Mo-CO bonds as a basis and generate a reducible representation using the character table. We therefore apply each operation to this basis and if a bond does not move we add a character of 1, if a bond is inverted it gets a character of -1, and if it moves we don't add anything to that character. Under the operation E, all three bonds are left unchanged so we give it a character of 3. Under the C3 operation, all of the bond vectors move, so we have a character of 0. Lastly, for the σv two bond vectors move and one stays in place, so we give it a character of 1. So our reducible representation is:
| E | C2 | σv (xz) | σ'v (yz) | |
|---|---|---|---|---|
| Γ | 3 | 1 | 0 | 3 |
This reduces into Γ= A1 + E. We can then determine from the character table that both of these will be IR and Raman active stretches.
Structure Determination
In chemistry, we are often concerned with the exact molecular structure of the compounds we are working with. We can use spectroscopy to further identify the structure of the molecule by considering the number of IR or Raman modes of vibration present. For example, Mo(CO)3(NCCH3)3 is can come in either its facial or meridional form (Figure 1) and therefore have different symmetries present - facial is C3v and meridional is C2v (C2v character table shown in Table \(PageIndex{2}\)). If we generate a reducible representation for the CO stretching vibrations in the meridional form, we get that:
| E | C2 | σv (xz) | σ'v (yz) | |
|---|---|---|---|---|
| Γ | 3 | 1 | 0 | 3 |
This can then be reduced to Γmer = 2A1 + E. All three of these stretching vibrations are IR active. If we compare that to the facial version: Γfac= A1 + E as determined above, we can see that the fac-Mo(CO)3(NCCH3)3 will have 2 IR active CO vibrational modes and mer-Mo(CO)3(NCCH3)3 has 3 IR active CO vibrational modes. This information can be used to distinguish between the two structures experimentally using IR spectroscopy. The same technique can be applied to Raman active modes.
Centrosymmetric Point Groups
We can further use Raman and IR spectroscopy to determine if our molecule has an inversion center present. This is because for molecules with an inversion center, all IR active modes are not Raman active and all Raman active modes are not IR active. This is known as the rule of mutual exclusion.
| E | 2C3 | 3σv | |||
|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | z | x2+y2, z2 |
| A2 | 1 | 1 | -1 | Rz | |
| E | 2 | -1 | 0 | (x,y), (Rx, Ry) | (x2-y2, xy), (xz, yz) |
| E | C2 | σv (xz) | σ'v (yz) | |||
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A2 | 1 | 1 | -1 | -1 | Rz | xy |
| B1 | 1 | -1 | 1 | -1 | x, Ry | xz |
| B2 | 1 | -1 | -1 | 1 | y, Rx | yz |


