1.13: Selection Rules for IR and Raman Spectroscopy
- Page ID
- 204714
Infrared Spectroscopy
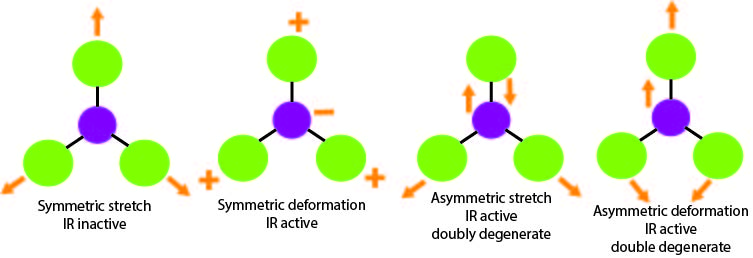
Infrared spectroscopy measures the frequency of absorption when a sample is irradiated with infrared electromagnetic radiation. It is a technique used to study the vibrations between atoms because atomic vibrational excitations occur in the infrared region of the electromagnetic spectrum. The bonds between atoms can be thought of as a spring connecting two masses. In the spring-mass analogy the moving system can be approximated by a simple harmonic oscillator. The frequency oscillation is proportional to \({\displaystyle {\sqrt {\frac {k}{m}}}}\),where k is the spring constant and m is the mass of the object. In a similar approximation, the frequency of vibration between two atoms is unique and varies depending on the strength of the bond (k) and the size of the atoms (m). When the frequency of electromagnetic radiation matches the natural frequency of vibration between atoms, the atoms are able to absorb this energy and exhibit vibrations. These vibrations can be detected as signals if they produce a change in the dipole moment between two atoms which can interact with the electric field. Representations for normal modes of vibration will be active in the infrared if they transform similar to any one of the cartesian coordinates (x,y,z). This would mean the vibrational motion has shifted the charge distribution in any of the x, y, or z directions resulting in a change in the dipole moment. Selection rules such as these are used to tell us whether such transitions are allowed, and therefore observed, or whether they are forbidden.
Raman Spectroscopy
Unlike IR spectroscopy which measures the energy absorbed, Raman spectroscopy consists of exposing a sample to high energy monochromatic light that interacts with the molecule and causes electronic, vibrational, or translational excitations. Upon interaction, the energy of the light is shifted either up or down and these changes can give information about the molecule’s various vibrational states. A photon of light excites the molecule to an excited state and upon relaxation to a different rotational or vibrational state the molecule emits a photon of a different energy. A vibration will give rise to a Raman shift, due to a shift from the incident light, if it has the same symmetry as the molecular polarizability. Polarizability measures the ability for a molecule’s electron cloud to become distorted. A dense electron cloud is more difficult to change than a more spread out electron density. The representation for one of the normal modes of vibration will be Raman active if it transforms similarly to the direct products of any one of the x, y, or z coordinates. That includes any of the functions: xy, xz, yz, x2, y2, z2, or any combination.
Rule of Mutual Exclusion
A molecule is centrosymmetric if it has a center of inversion and their corresponding point group contains the class for inversion. In such cases, the unit vectors transform as ungerade, or unsymmetric about the center of inversion, and direct products transform as gerade, or symmetric about the center of inversion. As a result, the normal modes of vibrational will show frequencies in either the IR or Raman, but the same frequency will not be observed in both.
Boron Trifluoride or D3d point group
| D3d | E | 2C3(z) | 3C'2 | σh (xy) | 2S3 | 3σv | Linear Functions/ Rotations | Quadratic Functions | Cubic Functions |
|---|---|---|---|---|---|---|---|---|---|
| A'1 | +1 | +1 | +1 | +1 | +1 | +1 | - | x2+y2, z2 | x(x2-3y2) |
| A'2 | +1 | +1 | -1 | +1 | +1 | -1 | Rz | - | y(3x2-y2) |
| E' | +2 | -1 | 0 | +2 | -1 | 0 | (x,y) | (x2-y2, xy) | (xz2, yz2) [x(x2+y2), y(x2+y2)] |
| A"1 | +1 | +1 | +1 | -1 | -1 | -1 | - | - | - |
| A"2 | +1 | +1 | -1 | -1 | -1 | +1 | z | - | z3, z(x2+y2) |
| E" | +2 | -1 | 0 | -2 | +1 | 0 | (Rx, Ry) | (xz, yz) | [xyz, z(x2-y2) |
Normal Modes of Vibration for D3d:
