2.9D: High Coordination Numbers
- Page ID
- 2534
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Coordination numbers from 2 to 6 and the associated coordination complexes are very common, especially in transition metal chemistry. These complexes can take on a variety of geometries and each individual complex will have unique properties based on its substituents and their arrangement spatially. Though there is no set number of ligands, ions, or bound atoms required for a species to be considered "highly coordinated" versus general coordination, when the coordination number exceeds seven it is generally considered a high coordination number. High coordination numbers are of particular interest in solution phase and inorganic chemistry.
Introduction
The coordination number of a specified atom in a chemical species is the "number of other atoms directly linked to that specified atom."[1] Coordination itself is "the formation of a covalent bond, the two shared electrons of which have come from only one of the two parts of the molecular entity linked by it, as in the reaction of a Lewis acid and a Lewis base to form a Lewis adduct; alternatively, the bonding formed in this way."[2] Coordination number is a measure of one of two things:
- In a molecule, the coordination number is simply the number of bound atoms to that molecule.
- For an ion the coordination number is the number of ions that are either associated to, or can associate with a given ionic species.
- Coordination requires a sigma bond be present or available to be present, and so a pi bond does not contribute to the coordination number of a species.
Lower Coordination Numbers
Following are a few examples of more commonly encountered coordination numbers
Coordination Number 2
Coordination numbers of two are more common in organic molecules, or in non transition-metal containing species and relatively rare in transition metal containing species. Coordination numbers of two result in a linear or collinear spacial arrangement.
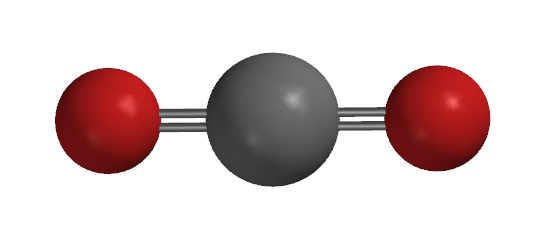
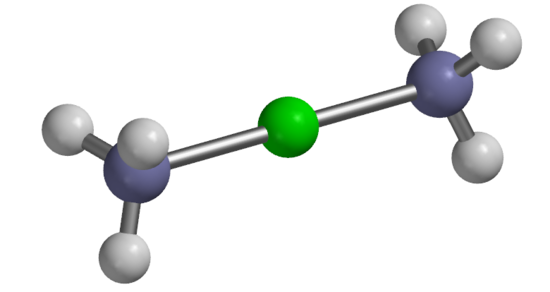
Carbon Dioxide, Coordination Number 2 [Ag(NH3)2]+, Coordination Number 2
Coordination Number 6
Coordination number 6 is the most common coordination number, especially among transition metal containing species.[4]
Generally, the octahedron is the preferred coordination geometry. Other possible coordination geometries exist for coordination number six, such as trigonal prismatic.

[Co(H2O)6)]3+, Coordination number 6
Higher Coordination
Higher coordination numbers; 7,8, 9, and above exist though they are less common.
Coordination Number 7
Seven coordinated atoms or molecules results in three main geometries:
- Pentagonal bipyramid
- Capped octahedron
- Capped trigonal prism
Coordination Number 8
Eight coordinated atoms or molecules results in two main geometries:
- Square antiprism
- Dodecahedron
Coordination Number 9
The only structure yet identified for coordination number 9 systems is the tricrapt trigonal prism.
Two examples of these structures are [ReH9]2- and [TcH9]2- with the representative geometry shown below.
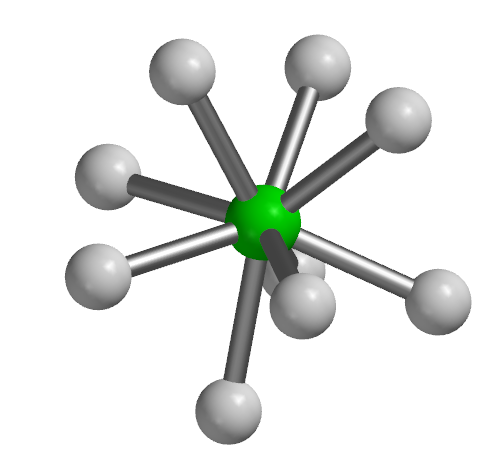
[TcH9]2-, Coordination number 9
Higher Coordination Numbers
Species exist with 10, 11, and 12 coordination numbers.
- Coordination numbers 10 and 11 are unique to complexes involving lanthanides and actinides. [4]
- Coordination number 12 has a structure that is involved in boron chemistry, the icosahedron.
- Coordination number 15 is the highest reported coordination number currently, being described for [PbHe15]2+[3]
References
- International Union of Pure and Applied Chemistry. "Coordination Number". Compendium of Chemical Terminology Internet edition.
- International Union of Pure and Applied Chemistry. "Coordination". Compendium of Chemical Terminology Internet edition.
- Hermann, A., Lein, M. and Schwerdtfeger, P. (2007), The Search for the Species with the Highest Coordination Number. Angewandte Chemie International Edition, 46: 2444–2447. doi: 10.1002/anie.200604148
- Housecroft, Catherine E.; Sharpe, Alan G., Inorganic Chemistry, 3rd Ed. Pearson Education Limited 2008
Problems
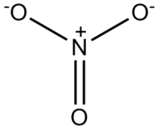
1. What is the coordination number of the nitrate ion NO3-?
2. What is the coordination number around Co in this complex? How many different ligands are around Cobalt?

3. What coordination number do you expect [Th(NO3)6]2- to have? (Draw out a rough structure, remember lone pairs are required for coordination. What is the likely geometry for this?
Answers
1. Coordination number 3. Pi Bonds do not contribute to coordination number.
2. Coordination number 6. There is one ligand around Cobalt; EDTA is hexadentate.
3. Coordination number 12; Each NO3- ligand is bidentate. The likely geometry is icosahedral like other 12 coordination number species.
Contributors and Attributions
- Brian Atwood (UC Davis)

