2.9B: Octahedral Species
- Page ID
- 2566
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In inorganic chemistry, an octahedron is classified by its molecular geometry in which its distict shape is described as having six atoms, groups of atoms or electron pairs symmetrically arranged around one central atom, defining the vertices of an octahedron. The prefix octa, which means eight, comes from the fact that the molecule has eight symmetrical faces. All atoms are 90 degrees apart from one another, and 180 degrees apart from the atom, directly across and opposite from it. In regards to identifying each species, we will be looking at three separate unique shapes with different numbers of bond pairs and lone pairs. This allows us to distinguish and classifiy the octahedrals based on the following shapes: octahedral, square pyramidal, and square planar.
Introduction
To be able to understand and distinguish the difference between the three types of octahedral species and how they differ from one molecule to the next, it is essential to try to visualize shapes geometrically and in 3D. A simple comprehension of geometry is required to be able to imagine molecules in 3D, as well as having basic background knowledge of the concept of bonding pairs and lone pairs. This allows one to recognize and see the difference in the molecular design for each individual molecule. We will begin by describing the design of an octahedral and then continue on to the next two molecules.
An octahedral is best described as a central atom symmetrically arranged by six other atoms. What makes this molecule different from other species is the fact that it is surrounded by six, either the same or different, atoms. There are six bonding pairs in this molecule and no lone electron pairs. The molecule below has no lone pairs of electrons surrounding it, thus allowing it to have a distinct shape. In a three dimensional sense, we may think of a x, y, and z coordinate plane having both its positive and negative coordinate systems. Another way of looking at it would be in the sense that all the faces of the molecule are present; through this reference, it resembles what would be a three dimensional prism. All the atoms are spread apart 90 degrees from each other and 180 from the atom directly across and opposite from it. The reson for the spacing is due to the molecule arranging itself in the most stable form possible, limiting the bond-pair to bond-pair interaction. Here is basic, but clear example of what an octahedral looks like:
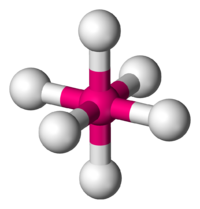
Octahedral (6 bond pairs and 0 electron pairs)
The next molecule that we will examine is known as a square pyramidal. This molecule has a lot of the same characteristics as that of an octahedral in the sense it consist of a central atom that is still symmetrically surrounded by six other atoms. What makes this molecule different from the previous molecule is the fact that this molecule does not consist of only bond-pair atoms surrounding it. There is one pair of electrons that has taken the place of one of the atoms and because these electrons are now present, it gives the molecule a distict new look. There are five bonding pairs and one electron pair. The atoms have to arrange themselves in the most stable form possible, not only limiting the bond-pair to bond-pair interaction, but also limiting the bond-pair to electron-pair interaction. The easiest way to visualize what this molecule looks like to visualize the x, y, and z coordinate plane again, but this time remove what would be considered the negative y coordinate axis and put a pair of lone pair electrons in its place. The molecule is still considered apart of the octahedral species because it still satisfies the 6 atom requirement, but in terms of its shape, the electrons effect the shape. This allows it to have its new shape. If you actually exclude those electrons and lay the molecule on the surface, you can see that it looks like a three dimensional pyramid with a square base. Again all the atoms and electron pair are 90 degrees apart from each other and 180 from the atom directly across and opposite from it. Here is what a square pyramidal would look like:
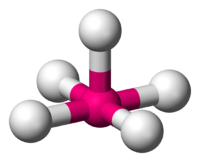
Square Pyramidal (5 bond pairs and 1 electron pair)
The last of the octahedral species is known as a square planar. This molecule resembles both of the previous molecules, but more similarly resembles a square pyramidal. It still has many of the characteristics of a square pyramidal, but what makes it different is that rather than having only one pair of electrons replacing the position of an atom, there are two pairs of electrons that are replacing the position of two atoms. To visualize what this molecule looks like, we refer back to the x, y, and z coordinate system, the only difference is this time we are taking away the entire y coordinate, and replacing it with electrons on what would be the positive y coordinate axis as well as placing a pair of electrons in what would be considered the negative y coordinate axis. The reason for this arrangement goes back to having the molecule arrange itself in the most stable form possible limiting interactions between bond-pair to bond-pair, bond-pair to electron-pair, and electron-pair to electron-pair. If you try visualizing what this would look like, it almost resembles a three-dimensional "X" with two pairs of lone electrons. Because the lone pairs of electrons are still present, that allows this molecule to still be considered an octahedral due to the fact that it still meets the requirements of being surrounded by 6 atoms or groups. In regards to its shape the electron pairs cause repulsion, thus allowing it to have its new shape. The atoms and electrons are still 90 degrees apart from eachother and 180 degrees from the atom directly across and opposite from it. Here is what a square planar would look like:
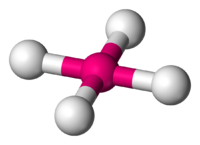
Square Planar (4 bond pairs and 2 electron pairs)
Heading #2
Rename to desired sub-topic. You can delete the header for this section and place your own related to the topic. Remember to hyperlink your module to other modules via the link button on the editor toolbar.
References
- Brown, Theodore L. Chemistry: the Central Science. 10th ed. Upper Saddle River, NJ: Pearson Prentice Hall, 2006. Print.
- Housecroft, Catherine E., and Alan G. Sharpe. Inorganic Chemistry. 3rd ed. Harlow: Pearson Education, 2008. Print. (Pgs 51-52)
Outside Links
- Sample octahedral image adapted from Wikipedia key word octahedral geometry:en.Wikipedia.org/wiki/Octahedral_molecular_geometry
- Sample square planar image adapted from Wikipedia key word square planar geometry:en.Wikipedia.org/wiki/Square_planar_molecular_geometry
- Sample square pyramidal image adapted from Wikipedia key word square pyramidal geometry:en.Wikipedia.org/.../Square_pyramidal_molecular_geometry
Problems
1. What causes the three different octahedral species to arrange the way they do? What conditions must be met?
2. Can two seperate electron-pair stand at 90 degrees apart from eachother? Why?
3. Give one example of a molecules that would fall into the category of a octehedral, square pyramidal, and square planar.
Answers
1. The molecules take the arrangment they do due to trying to arrange themselves in the most stable structure possible limiting the interaction between bond-pair and electron-pair interaction. As long as these conditions can be met, it is possible for the structure to not only exist, but remain stable.
2. This again goes back to satisfying the conditions of keeping the molecule as stable as possible by limiting lone-pair to lone -pair interaction as well as same sign interaction. Because electrons hold the same kind of charge, they can not be near eachother due to same charge repulsion and so they need to be as far away as possible from eachother so that the molecule may be stable.
3. Molecules that would fall into the category of triganol planar based on their molecular geometry would be SF6, a molecule that falls into the category of a square pyramidal would be BrF5 and one molecule that would fall into a category of a square planar would be [AuCl2]-.
Contributors and Attributions
- Name #1 here (if anonymous, you can avoid this) with university affiliation

