3.2.3: Electronegativity and Atomic Size Effects
- Page ID
- 219071
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
We saw in previous sections how lone pairs of electrons and multiple bonds distort bond angles between non-central atoms (ligands) around a central atom. This section describes how ligand electronegativity and size also influence bond angles and molecular geometry. Electronegativity is generally correlated with atomic size going down any group of the periodic table. There are some cases where bond angles can be predicted by these correlations. However, size and electronegativity can also work as competing factors in determining bond angles.
Definitions of Electronegativity
Linus Pauling introduced the first electronegativity scale in 1932 in order to explain the extra stability of molecules with polar bonds.[1] The electronegativity of an atom, represented by the Greek letter \(χ\) (chi), can be defined as the tendency of an atom to draw electrons to itself in a chemical bond. On the Pauling scale, the electronegativity difference between two atoms A and B was defined in terms of the dissociation energies Ed of the A-A, B-B, and A-B bonds:
\[\chi_{A} - \chi_{B} = \sqrt{E_{d}(AB) - [E_{d}(AA) + E_{d}(BB)]/2} \nonumber \]
where the energies are expressed in electron volts. Pauling's scale of electronegativity ranges from Fluorine (most electronegative = 4.0) to Francium (least electronegative = 0.7). [2,3] The polarity of bonds and assignment of formal charges is predicted by electronegativity differences.
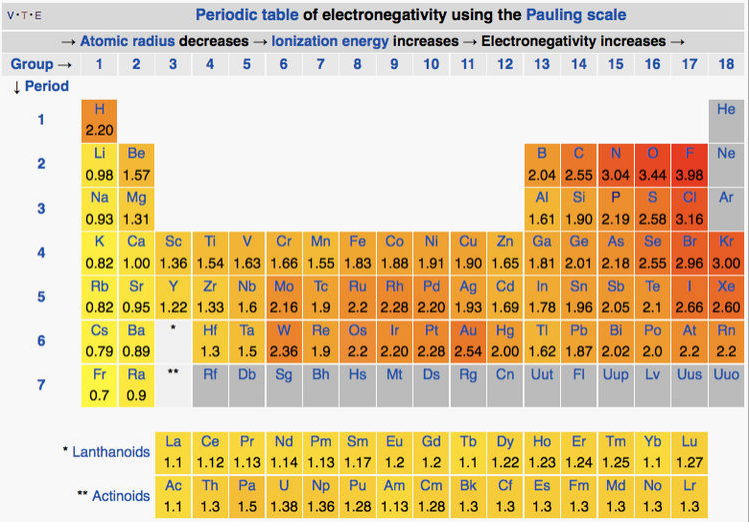
While directly relevant to the strength of chemical bonds, the Pauling definition of electronegativity has a significant limitation: calculating each value requires data from several compounds in which specific atoms are bonded. This means that the scale cannot be successfully applied to all situations. To overcome this limitation, alternative electronegativity scales were developed based on different thermochemical measurements or calculations. These other scales are listed in the table below. More thorough descriptions of how values in each scale are calculated are described on Wikipedia's Electronegativity page (click) and a concise history of electronegativity scales is summarized in ref 4.
| Scale Developer | Year first described | Characteristics |
|---|---|---|
| Linus Pauling[1] | 1932 | Based on bond energies |
| Robert S. Mulliken[5,6] | 1934 | Based on valence electron properties of atoms (electron affinity and ionization energy) |
| Louis Allred & Eugene G. Rochow[7] | 1958 | Based on electrostatic force (effective nuclear charge) |
| Robert T. Sanderson[8] | 1983 | Based on atomic electron density |
| Ralph G. Pearson[9] | 1985 | Related to Hard-Soft Acid-Based theory |
| Leland C. Allen, Joseph Mann, Terry L. Meek[10,11,12] | 1989, 2000 |
Average ionization energies of valence shell electrons, configuration energies (CE)\[\mathrm{CE}=\frac{n \varepsilon_{s}+m \varepsilon_{p}}{n+m} \nonumber \] \(n = \text{number of s electrons}\) |
The primary advantage to this scale developed by Mann, Meek, and Allen[12] is that it is based on configuration energy (CE), the average ionization energies of valence electrons in ground state free atoms. A scale based on ionization energies can be calculated more directly for any element. However, a critique of all electronegativity scales, including this one, is that they are all based on assumptions that fail in some cases.
There is a relationship between electronegativity and atomic size because both are related to ionization energy. Like ionization energy, there is a general trend across the periodic table for both electronegativity and atomic size; in general, smaller atoms toward the top right-hand side of the periodic table have greater electronegativity values and smaller atomic size. We will see below that both electronegativity and atomic size influence bond angles and absolute molecular geometry around a central atom. In some cases, the size and electronegativity affects are aligned; in some cases these effects compete.
Electronegativity and Size Influence Bond Angles
Let's begin by examining the bond angles of several trigonal pyramidal molecules. The molecules shown in Figure \(\PageIndex{2}\) each have three identical "pendant groups" on the central atom (Figure \(\PageIndex{2}\)). Pendant atoms or pendant groups are the atoms, or groups of atoms, that are bonded directly to the central atom. The molecules shown here are arranged according to the size of the central and pendant atoms. Central atoms increase in size going down this figure, and pendant atoms increase in size going across from left to right. The bond angles and bond lengths are labeled in each case.
What trends can you identify?
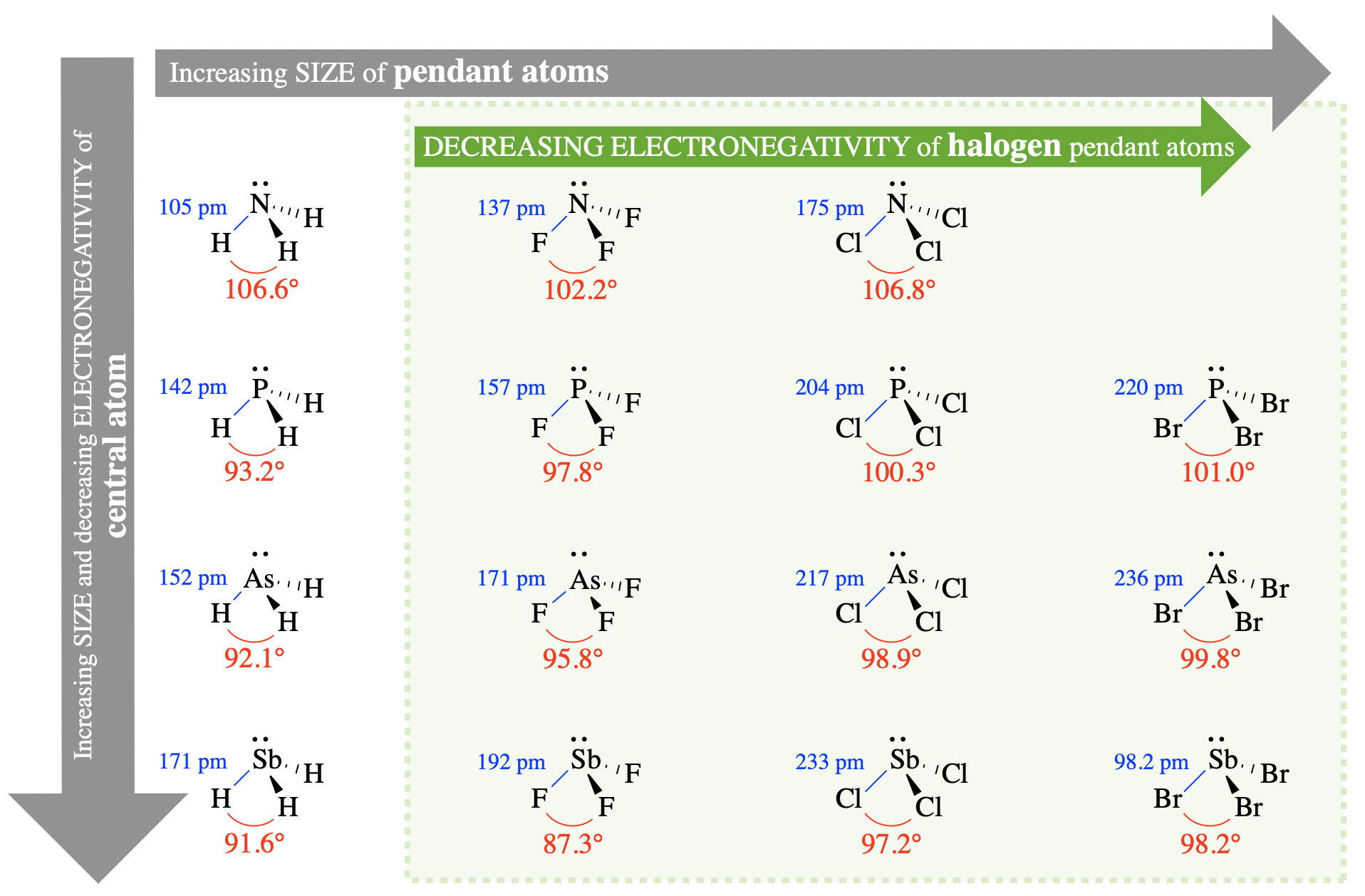
Trends in Size
First, let's examine how the size of the central and pendant groups might influence bond angle. In VSEPR theory, the size of atoms (or groups of atoms) will affect bond angles due to changes in steric interactions between pendant groups.
Size of the central atom
Examine the relationship between the size of the central atom and the bond angles in Figure \(\PageIndex{2}\) (go down any column in the figure). For example, compare NH3, PH3, AsH3, and SbH3, with bond angles 106.6°, 93.2°, 92.1°, and 91.6°, respectively. In this series, the size of the central atom increases from N to Sb while the size of the pendant atom (hydrogen) remains constant. As the size of the central atom increases, the bond angles decrease; thus, we observe a negative relationship between size of the central atom and the bond angle in these molecules. This relationship is explained by sterics. As the central atom increases in size, the bond lengths also increase and the pendant atoms are farther from each other in space. In VSEPR theory, this will reduce steric interactions between the pendant groups. Since the lone pair on these molecules is more repulsive than bonded groups, the decrease in steric interactions between bonded groups results in a decrease in bond angles.
Size of the pendant atoms (or groups)
Examine the relationships between size of the halogen pendant atoms and bond angle in Figure \(\PageIndex{2}\) (go across any row within the shaded region). For example, compare PF3, PCl3, and PBr3, with bond angles 97.8°, 100.3°, and 101.0°, respectively. In this series, the size of the pendant atom increases from F to Br while the central atom remains constant (phosphorous). As the size of pendant atoms increases, the bond angle increases; thus, we observe a direct relationship between size of the pendant group and the bond angle in these molecules. Again, we can explain this using sterics. As the size of the pendant atoms increases, sterics between the pendant groups will increase (despite small changes in bond length). Increased steric interactions between pendant groups will prefer larger bond angles between the groups.
This trend fails, however, if we consider the molecules with hydrogen as the pendant atoms. Notice, for example, that H is the smallest pendant atom. If we consider the trend described above, we should assume that XH3 (where X is a variable atom) would have the smallest bond angle in the series of XH3, XF3, XCl3, and XBr3. However this is not the case of NH3, NF3, and NCl3, with bond angles 106.6°, 102.2°, and 106.8°, respectively. To explain the variation in these bond angles, we need to consider electronegativity.
Trends in Electronegativity
Now let's examine how electronegativity influences bond angles around a central atom. In VSEPR theory, electronegativity of atoms/groups will affect bond angles due to changes in the distribution of electron pairs around the central atom (and thus changes in the severity of electron pair repulsion). This really comes down to bond polarity caused by the difference in electronegativity between the central atom and pendant groups (bond polarity in the context of valence bond theory). In a polar bond, the more electronegative atom will pull electron density towards itself. When a pendant atom is more electronegative, it will pull the bonded electron pair towards itself and away from the central atom; this will reduce the electron pair repulsion between bonded electron pairs on the central atom. A decrease in electron pair repulsion on the central atom should decrease bond angles between the groups (Figure \(\PageIndex{3}\)).
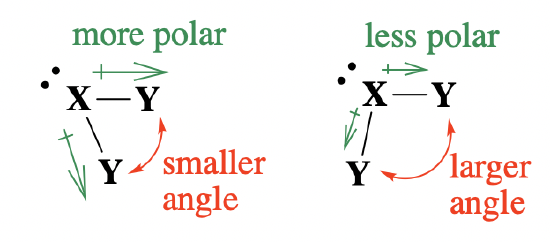
Electronegativity is an alternative explanation to the trends we already examined above in Figure \(\PageIndex{2}\) . For example, when we compare the halogen pendant atoms (shaded region in Figure \(\PageIndex{2}\)) , the electronegativity of pendant groups decreases, bond polarity of the bonds decreases, and bond angles increase going from left to right and from F to Br. As more electron density remains on the central atom, electron repulsion between the bonded pairs increases and bond angles increase.
The electronegativity argument can also be used to explain the fact that NH3 (106.6°) has a larger bond angle than NF3 (102.2°). This particular case illustrates how electronegativity and size can be competing factors. While electronegativity differences seem to dominate in the case of NH3 (106.6°) compared to NF3 (102.2°), size differences still dominate in the cases of other XH3 and XF3 examples in Figure \(\PageIndex{2}\)).
Predict the geometry and approximate bond angles. Then put the molecules in each series in order of smallest to largest bond angle. Defend your answer.
- The X-S-X bond angle in OSF2, OSCl2, OSBr2
- H2O, H2S, H2Se, H2Te
- H2O, OF2, OCl2
- Answer (a)
-
Geometry and predicted bond angles: These are molecules with steric number 4. They can be written as two different resonance structures, and the resonance hybrid would have double bond character between S and O.
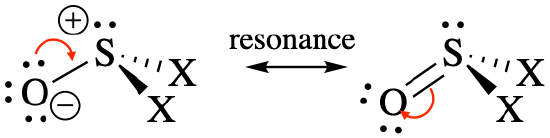
We would expect a trigonal pyramidal geometry with all bond angles <109.5° because the lone pair is more repulsive than bonds. Because the double bond is more repulsive than single bonds, we should also expect the O-S-X bond angles to be greater than the X-S-X bond angles.
Trend: This is a series of molecules that varies in the identity of the pendant atoms; the variation is within the halogens. The size of the halogens increases, and the electronegativity decreases in the order F, Cl, Br. Both size and electronegativity would lead us to conclude that the X-S-X bond angles would increase in the order OSF2 < OSCl2 < OSBr2
Explanation: (1) Increasing electonegativity of the pendant atom (F > Cl > Br) increases the polarity of the bond and reduces the electron density of the bonded pair on the central atom. This reduces the e-e repulsions of adjacent bonded electron pairs on S, allowing the halogens to become closer. The more electronegative pendant atoms can have smaller bond angles. (2) Increasing size of pendant atoms (F < Cl < Br) increases steric repulsions and increases bond angle. Both explanations lead to the same predicted trend.
The actual measured X-S-X bond angles are OSF2 (92.3°) / OSCl2 (96.2°) / OSBr2 (98.2°). The trend in these bond angles is consistent with the prediction.
- Answer (b)
-
Geometry and predicted bond angles: These are molecules with steric number 4, bent molecular geometry, with predicted bond angles <109.5° because the two lone pairs are each more repulsive than the bonds. There are two lone pairs and two single bonds to H around each central atom.
Trend: This is a series of molecules that varies in the identity of the central atom. The central atom increases in the order O < S < Se < Te, where Te is the largest element and O is the smallest. Arguments based on size would lead us to predict that the pendant groups of H2Te would be less sterically crowded and thus have a smaller bond angle than the pendant groups of H2O. The electronegativity decreases in the order O > S > Se > Te, where O is the most electronegative element and Te is the least. Thus, we expect the bonding electro pairs to be closer to the central atom on O than they would be on Te; we should expect H2Te to have the least electron pair repulsions and thus smallest bond angle in this series, while H2O would have the strongest electron pair repulsions and largest bond angles.
Both arguments lead to the same conclusion, that the order of increasing bond angle is H2Te < H2Se < H2S < H2O.
The actual measured bond angles are H2Te (90.2°) / H2Se (90.6°) / H2S (92.1°) / H2O (104.5). The trend in these bond angles is consistent with prediction.
- Answer (c)
-
Geometry and predicted bond angles: These are molecules with steric number 4, bent molecular geometry, with predicted bond angles <109.5° because the two lone pairs are each more repulsive than the bonds. There are two lone pairs and two single bonds to H around each central atom. (This is similar to the case in (b)).
Trend: This is a series of molecules that varies in the identity of the pendant atoms; two of the molecules have halogens, and the other has hydrogen pendant atoms. This is a case where size and electronegativity will be conflicting factors because trends in electronegativity do not mirror the trend in size.
- Size: The size of pendant atoms increases in the order H < F < Cl where H is smallest and Cl is largest. Prediction of bond angles based on size alone would lead to the predicted order of increasing bond angle H2O < OF2 < OCl2.
- Electronegativity: The electronegativity decreases in the order F > Cl > H where F has the greatest electronegativity and H has the least. Since we expect the most electronegative pendant atoms to have the smallest bond angles, prediction based on electronegativity alone would lead to the predicted order of increasing bond angle OF2 < OCl2 < H2O.
The points above illustrate how the two different arguments would lead to different predictions about the trend in bond angle. This makes it difficult to predict the actual order of increasing bond angle. However, we saw above in the example of NH3 vs NF3 that electronegativity is more important than size; yet in the case of NH3 vs NCl3, the much larger size of the pendant atom is more important. If we apply this lesson to the current problem, we might predict the order OF2 < H2O< OCl2 , and in fact this more nuanced prediction, based on a similar case, matches the actual order for measured bond angles: OF2 (103.3°) < H2O (104.5°) < OCl2 (110.9°).
Group Electronegativities
You probably heard the terms "electron donating group" and "electron withdrawing group" from your coursework in Organic Chemistry. For example, the acid trifluoroacetic acid (TFA) is more acidic than acetic acid due to the electron withdrawing effects of the CF3 group compared to CH3. CF3 is an electron withdrawing group, while CH3 is an electron donating group. In other words, CF3 is more electronegative than CH3.
The electron withdrawing ability (electronegativity) of groups can be estimated and compared, just as they are with atoms. Although there is no one scale that is used for group electronegativities, and published values even for the same groups vary widely, there are reliable trends within similar groups. The same size and electronegativity factors discussed above that affect bond angles for pendant atoms, also can be used to rationalize distorted bond angles for pendant groups around a central atom.
Consider the relative electronegativities and sizes of the pendant atoms/groups in the following examples. Is the trend in bond angles what you would expect from the relative group electronegativities and relative sizes? What, if any, is the more dominant factor in determining the trend?
- N(CH3)3 has an C-N-C bond angle of 110.9°, while N(CF3)3 has a bond angle of 117.9°.
- The X-S-X bond angles in molecules of the form SO2(X)2 are: SO2(OH)2 101.3°; SO2(CF3)2 102.0°; SO2(CH3)2 102.6°.
- Answer (a)
-
Add texts here. Do not delete this text first.
- Answer (b)
-
Add texts here. Do not delete this text first.
Special case of electronegativity and size in steric number 5 (trigonal bypyramid)
Molecules with steric number 5 are interesting because they posses two different types of positions (equatorial and axial). These positions have unique bond angles and bond lengths. Pendant atoms/groups have different preferences for the axial and equatorial positions that depend somewhat on their electronegativity.
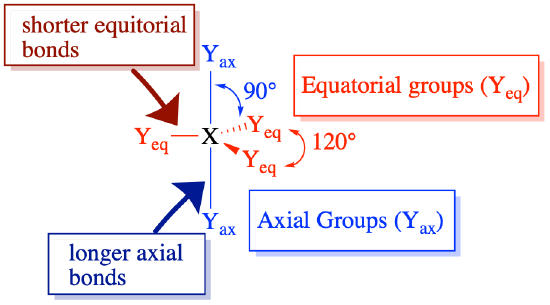
In a previous section, we discussed the preference of lone pairs and multiple bonds for the equatorial positions in trigonal bipyramidal molecules. VSEPR theory rationalizes this by assuming that lone pairs and multiple bonds are more repulsive than the electron pairs in single bonds. Equatorial positions are less crowded (with only two closest neighbors at 90°, and two farther neighbors at 120°) compared to axial positions (with three closest neighbors at 90°), thus the more repulsive groups prefer the less crowded equatorial positions.
Pendant groups that are more electronegative result in weaker electron pair repulsion around the central atom, while groups that are less electronegative result in stronger electron-pair repulsion around the central atom (as described above). The result for steric number 5: bonding pairs to less electronegative elements are more repulsive, and generally prefer equatorial positions. Still, lone pairs and multiple bonds are more repulsive than single bonds and would show a stronger preference for equatorial positions.
Examples and Nuances
Some examples of molecule that demonstrate the equatorial preference of less electronegative groups are below. Predict (draw) their structures.
- PF4Cl, PF3Cl2, and PF2Cl3
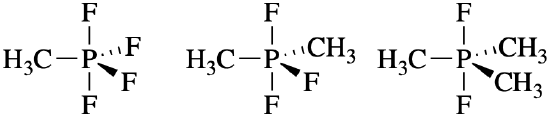
- PF4(CH3) PF3(CH3)2, and PF2(CH3)3
- Answer (a)
-
Cl is less electronegative than F; thus we expect Cl to have stronger preference for the equatorial positions.
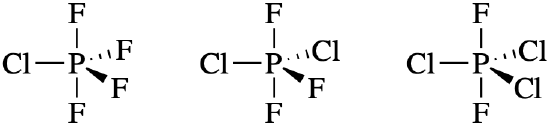
- Answer (b)
-
CH3, an electron donating group, is less electronegative than F. We expect CH3 to have a stronger preference for the equatorial positions.
In the exercise above, the structures can be explained by the electronegativity of the pendant groups; less electronegative groups prefer the equatorial positions. There are other similar molecules for which explanations (or predictions) are difficult. For example, the series of molecules below seems to have completely random placement of F and CF3 groups. These structures could not be predicted based on VSEPR theory. It seems that in this case, the more symmetrical arrangements of pendant groups is preferred.
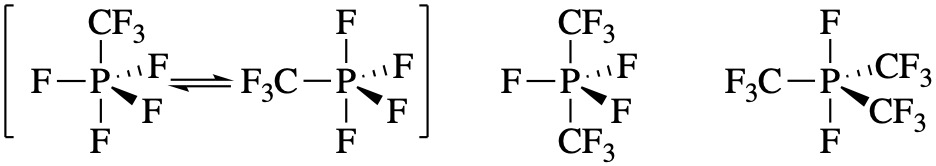
References and resources
- Pauling, L. (1932). "The Nature of the Chemical Bond. IV. The Energy of Single Bonds and the Relative Electronegativity of Atoms". J. Am. Chem. Soc. 54(9): 3570–3582. doi:10.1021/ja01348a011.
- Housecroft, Catherine E. et. al. "Inorganic Chemistry" 3rd Edition. Pearson Education Limited 2008. Chapter 2.5 "Electronegativity Values" pgs. 42-44
- International Union of Pure and Applied Chemistry. "Electronegativity". goldbook.iupac.org/E01990.html.
- Pearson, R.G. Acc. Chem. Res. 1990, 23, 1, 1–2. https://doi.org/10.1021/ar00169a001
- Mulliken, R. S. (1934). "A New Electroaffinity Scale; Together with Data on Valence States and on Valence Ionization Potentials and Electron Affinities". J. Chem. Phys.2 (11): 782–793. doi:10.1063/1.1749394.
- Mulliken, R. S. (1935). "Electronic Structures of Molecules XI. Electroaffinity, Molecular Orbitals and Dipole Moments". J. Chem. Phys. 3 (9): 573–585. doi:10.1063/1.1749731.
- Allred, A. L.; Rochow, E. G. (1958). "A scale of electronegativity based on electrostatic force". Journal of Inorganic and Nuclear Chemistry. 5 (4): 264–268. doi:10.1016/0022-1902(58)80003-2
- Sanderson, R. T. (1983). "Electronegativity and bond energy". Journal of the American Chemical Society. 105 (8): 2259–2261. doi:10.1021/ja00346a026
- Pearson, R. G. (1985). "Absolute electronegativity and absolute hardness of Lewis acids and bases". J. Am. Chem. Soc. 107 (24): 6801. doi:10.1021/ja00310a009.
- Allen, Leland C. (1989). "Electronegativity is the average one-electron energy of the valence-shell electrons in ground-state free atoms". Journal of the American Chemical Society. 111 (25): 9003–9014. doi:10.1021/ja00207a003.
- Mann, Joseph B.; Meek, Terry L.; Allen, Leland C. (2000). "Configuration Energies of the Main Group Elements". Journal of the American Chemical Society. 122 (12): 2780–2783. doi:10.1021/ja992866e.
- Mann, Joseph B.; Meek, Terry L.; Knight, Eugene T.; Capitani, Joseph F.; Allen, Leland C. (2000). "Configuration energies of the d-block elements". Journal of the American Chemical Society. 122 (21): 5132–5137. doi:10.1021/ja9928677
Acknowledgment
- Matthew Salem (UC Davis) (Pauling Electronegativity)
- Introduction to Inorganic Chemistry Wikibook (https://chem.libretexts.org/Bookshel..._Bond_Strength)
Curated or created by Kathryn Haas


