1.4: Bond Polarity and Bond Strength
- Page ID
- 183292
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Linus Pauling introduced the concept of electronegativity 1932 in order to explain the extra stability of molecules with polar bonds. [12] The electronegativity of an atom, represented by the Greek letter χ, can be defined as the tendency of an atom to draw electrons to itself in a chemical bond. On the Pauling scale, the electronegativity difference between two atoms A and B was defined in terms of the dissociation energies Ed of the A-A, B-B, and A-B bonds:
\[\chi_{A} - \chi_{B} = \sqrt{E_{d}(AB) - [E_{d}(AA) + E_{d}(BB)]/2}\]
where the energies are expressed in electron volts.
This definition, while directly relevant to the strength of chemical bonds, requires thermochemical input data from many compounds, some of which were not available at the time. Mulliken[13][14] and later Pearson[15] developed a scale of electronegativities based on the average of the electron affinity and ionization energy of the free A and B atoms, which they correlated with thermochemical data and the Pauling scale.
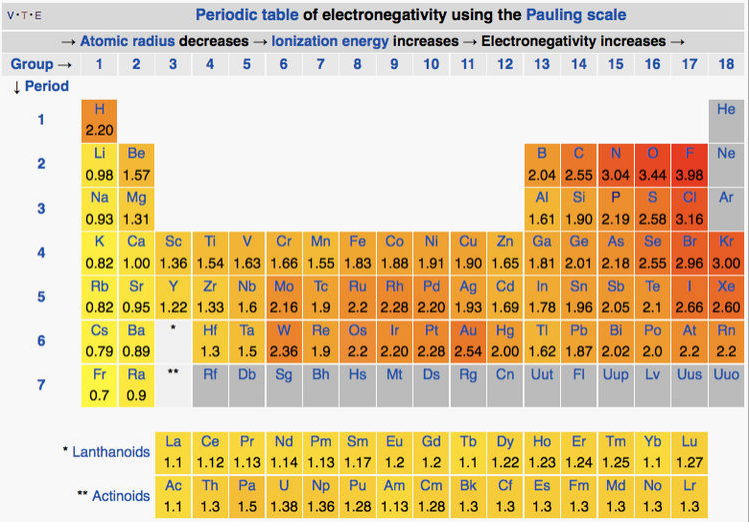
On the Pauling scale, the least electronegative elements are the alkali metals (χ = 0.7-1.0) and the most electronegative are oxygen (3.5) and fluorine (4.0) at the upper right of the periodic table. Carbon and hydrogen have intermediate electronegativities (2.6 and 2.2 on the Pauling scale, respectively). The general trend (see table below) is that electronegativities increase going up and to the right in the periodic table. There are some interesting exceptions to this behavior, most notably two islands of high electronegatvity at the bottom of the transition series, peaking at tungsten (χ = 2.4) and gold (χ = 2.5). The first of these can be explained by the very high metal-metal bond energy of elements such as Mo and W, which can use all six of their valence electrons in bonding, as we will discuss in Chapter 6. The second however occurs with more weakly bonded noble metals such as Pt and Au, and is responsible for their low position in the activity series,[16] as well as their extraordinary properties as catalysts.
Table of Pauling electronegativities
The polarity of bonds is determined by electronegativity differences. As a guideline we define bonds as:
- ionic if Δχ > 2.0
- polar if 2.0 > Δχ > 0.5
- nonpolar if 0.5 > Δχ
The polarity of bonds helps us understand non-covalent forces between molecules, such as hydrogen bonding and dipole-dipole interactions. It also helps us interpret the reactivity of molecules. For example, the Si-H bond (χSi = 1.8, χH = 2.1) is more hydride-like than the C-H bond (χC = 2.5, χH = 2.1). Therefore silanes react with acids to make H2, whereas phosphines (χP = 2.1) and hydrocarbons do not. Similarly, electrophilic substitution reactions occur more readily on Si-H and P-H compounds than they do on C-H compounds.
There is also a correlation between the strength of a chemical bond and the bond length, longer bonds being weaker because of weaker orbital overlap. Pauling introduced an empirical formula relating bond length to bond strength. For a given pair of atoms (for example, two carbon atoms):
\[D(n) = D(1) - 0.6 \log_{10}(n)\]
where D(n) represents the bond length in Å and n is the bond order. D(1) in this case would be the length of a C-C single bond, which we can obtain from the average bond length in alkanes (1.54 Å). Using this formula we can predict that the bond lengths in ethylene (C=C double bond) and acetylene (C≡C triple bond) should be 1.36 and 1.25 Å, respectively, which are close to the experimental values of 1.33 and 1.20 Å. In a related form the Pauling formula can be used to calculate bond lengths when the single bond length D(1) is not available:
\[D(n) = D(m) -0.6 \log_{10}(n/m)\]
Here n and m represent two different bond orders between the same kinds of atoms. This tells, for example, that the difference in length between a triple and double bond, D(2)-D(3), should be - 0.6 log10(2/3) = 0.11 Å. Some bond lengths and bond energies are anomalous. For example, the F-F bond length in F2 is 1.43 Å, which is 0.15 Å longer than twice the covalent radius of the F atom (0.64 Å). The F-F bond is also quite weak (bond dissociation energy = 155 kJ/mol) relative to the Cl-Cl bond (242 kJ/mol). By putting the extra bond length into the Pauling formula, we calculate that the bond order in the F2 molecule is only 0.6, i.e., substantially weaker than a F-F single bond. The physical reason for this is that the F-F bond is "stretched" by repulsion of the lone pairs on the F atoms. This crowding is caused by the fact that the [He] 1s2 core orbital, as well as the valence orbitals of the fluorine atoms, are contracted by the high nuclear charge. The Cl2 atom, with its larger [Ne] (1s22s22p6) core, in contrast, has a "normal" single bond length (1.98 Å) that is twice the covalent radius of the Cl atom (0.99 Å). A similar lone pair repulsion effect explains the anomalously long and weak N-N and O-O single bonds in hydrazine (H2N-NH2) and hydrogen peroxide (HO-OH), which are both highly reactive molecules.
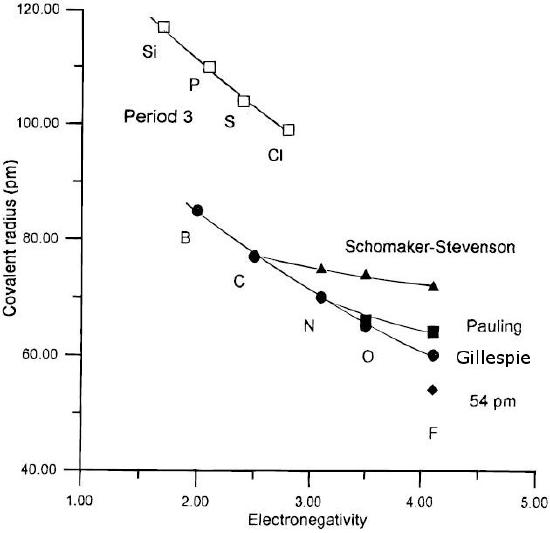
The important roles of electronegativity differences and lone pair repulsion are evident when comparing trends in bond strengths. The table below shows the average single-bond enthalpies of p-block elements with H and F. H makes stronger bonds with 2nd row elements (C, N, O, F) than with third row elements (Si, P, S, Cl) because the 2p valence electrons are closer to the nucleus and thus make stronger bonds than electrons in 3p orbitals. The bonds to H also follow the expected trend of increasing bond strength with increasing electronegativity difference. Bonds between second row elements (C, N, O, F) and F are however anomalously weak because of lone pair repulsion. For this reason, the Si-F bond is substantially stronger than the C-F bond, whereas the C-H bond is much stronger than the Si-H bond. The strong Si-F bond is the reason that HF etches glass (to produce the SiF62- anion), and the strong C-H bond is an important factor in the stability of hydrocarbons and other organic molecules.
| C-H 413 | N-H 391 | O-H 483 | H-F 567 |
| Si-H 323 | P-H 322 | S-H 339 | H-Cl 431 |
| C-F 485 | N-F 272 | O-F 190 | F-F 155 |
| Si-F 565 | P-F 490 | S-F 327 | Cl-F 253 |
The anomalously weak bond in F2 is responsible for the high electronegativity of fluorine, as well as the legendary reactivity of elemental fluorine gas, which reacts explosively with hydrogen and powdered metals. Because of the instability of elemental fluorine and the polar nature of its bonds with more electropositive elements, fluorine compounds tend to be very stable. For example, the noble gases Xe and Kr react with fluorine to make covalent compounds, whereas other halogens do not react. Fluorocarbon compounds contain strong C-F bonds and have high thermal and chemical stability. Perfluorocarbons such as Teflon (poly(tetrafluoroethylene), -(CF2CF2)n-, PTFE) are also highly hydrophobic. The extraordinary hydrophobicity of perfluorocarbons arises from the fact that -CF2- and -CF3 groups are "fatter" than -CH2- and -CH3 groups; dissolving them in water is therefore more disruptive to the hydrogen bonding network than is dissolving a hydrocarbon. [21]



