3.2.4: Ligand Close Packing
- Page ID
- 222357
Introduction
Ligand Close Packing (LCP) theory is complimentary to VSEPR, except that LCP focuses on repulsions between pendant atoms ("outer" atoms that are not directly bonded to one another), rather than focusing on the chemical environment around the central atom in a molecule. Both LCP and the VSEPR models were developed by Robert Gillespie.
The LCP model assumes that ligands (or pendant atoms) "pack" as closely as possible around a central atom. A given ligand will have a specific atomic radius when bound to a central atom. The distance between two ligands around the same central atom is simply the sum of the atomic radii of the pendant atoms. Therefore for a specific set of ligands around a specific central atom, the ligand-ligand distances are constant despite the coordination number or bond angles. In other words, for a series of similar molecules with the same central atom, while bond angles and bond distances of pendant atoms may change, the distances between two pendant atoms remain the same.
According to LCP, distances between two pendant atoms are similar...
- even when steric number changes
- even when bond angles change
- Reason: pendant atoms "pack" around the central atom.
Ligand Close Packing and Bond Distances
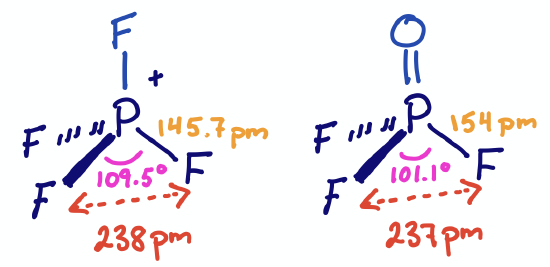
If the distance between non-bonded atoms remains constant even while bond angles change, then the bond length between the pendant and central atom must change to accommodate. For example, \(\ce{PF4+}\) and \(\ce{PF3O}\) have almost identical \(\ce{F - F}\) distances of 238 and 237 pm, respectively. As expected from VSEPR, the \(\ce{F - P - F}\) bond angle in \(\ce{PF4+}\) is 109.5°. The \(\ce{F - P - F}\) bond angle in \(\ce{PF3O}\) (101.1°) is smaller due to the increased repulsion of the oxygen double bond. Therefore the P-F bond lengths must be different. In fact, the P-F bond distances are 145.7 pm in \(\ce{PF4+}\) and 154 pm in \(\ce{PF3O}\).
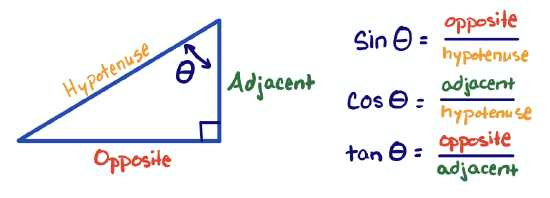
The relationship between bond angles, bond lengths, and close-packing distance is described by right angle trigonometry (recall SOA-CAH-TOA). In a right triangle, the hypotenuse is the longest side, opposite to the right angle. For either of the other two angles in the triangle, the angle (\(\theta\)) and lengths of the sides (opposite and adjacent to \(\theta\)) are related by the trigometric functions shown in Figure \(\PageIndex{2}\) .
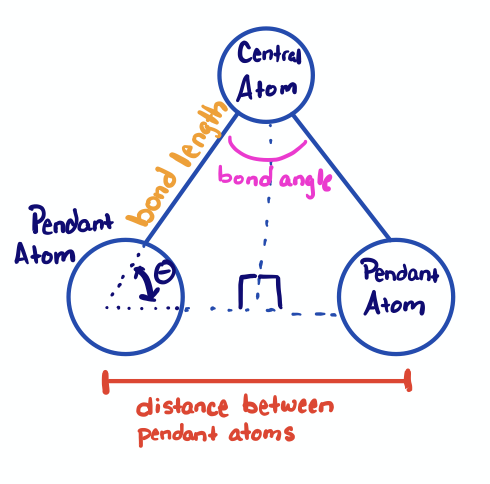
In the case of a molecule, we can apply right angle trigonometry by imagining that the bond angle is divided into two right angles, as illustrated in Figure \(\PageIndex{2}\). The hypotenuse of the triangles is the bond length, the opposite side is one half of the close-packing distance, and \(\theta\) is one half the bond angle.
The distance between F atoms is 212 pm in both \(\ce{NF4+}\) and \(\ce{NF3}\). The bond angles are 109.5° and 102.3°, respectively. What are the expected \(\ce{N - F}\) bond lengths?
- Answer
-
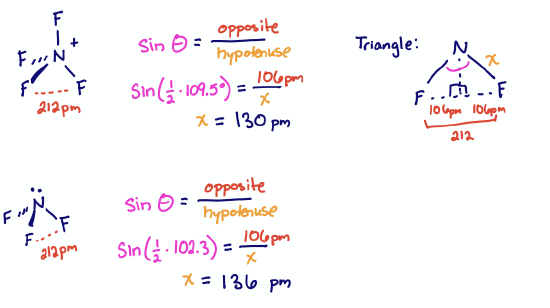
The actual measured bond lengths are 130 pm for \(\ce{NF4+}\) and 136.5 pm for \(\ce{NF3}\).


