Skip to main content
Chemistry LibreTexts

3.2: Valence Shell Electron-Pair Repulsion

  1. Last updated
  2. Save as PDF
  • Page ID
    166735

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Introduction to VSEPR

    The Valence Shell Electron Repulsion (VSEPR) model can predict the structure of most molecules and polyatomic ions in which the central atom is a nonmetal; it also works for some structures in which the central atom is a metal. VSEPR builds on Lewis electron dot structures (discussed in Section 3.1); Lewis structures alone predict only connectivity while the Lewis structure and VSEPR together can predict the geometry of each atom in a molecule. The main idea of VSEPR theory is that pairs of electrons (in bonds and in lone pairs) repel each other. The pairs of electrons (in bonds and in lone pairs) are called "groups". Because electrons repel each other electrostatically, the most stable arrangement of electron groups (i.e., the one with the lowest energy) is the one that minimizes repulsion. Groups are positioned around the central atom in a way that produces the molecular structure with the lowest energy. In other words, the repulsion between groups around an atom favors a geometry in which the groups are as far apart from each other as possible. Although VSEPR is simplistic because it does not account for the subtleties of orbital interactions that influence molecular shapes, it accurately predicts the three-dimensional structures of a large number of compounds.

    We can use the VSEPR model to predict the geometry around the atoms in a polyatomic molecule or ion by focusing on the number of electron pairs (groups) around a central atom of interest. Groups include bonded and unbonded electrons; a single bond, a double bond, a triple bond, a lone pair of electrons, or even a single unpaired electron each count as one group. The molecule or polyatomic ion is given an AXmEn designation, where A is the central atom, X is a bonded atom, E is a nonbonding valence electron group (usually a lone pair of electrons), and m and n are integers. The number of groups is equal to the sum of m and n. Using this information, we can describe the molecular geometry around a central atom, that is, the arrangement of the bonded atoms in a molecule or polyatomic ion. The geometries that are predicted from VSEPR when a central atom has only bonded groups (n = 0) are listed below in Table \(\PageIndex{1}\). The cases where lone pairs contribute to the total groups (n \(\geq\) 1) are discussed in the next section about lone pair repulsion.

    Table \(\PageIndex{1}\). Geometries predicted using VSEPR theory (bonded groups only).

    Groups around central atom

    (m + n)

    		 Geometry Name Geometry Sketch Predicted bond Angle Example
    2 linear 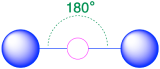clipboard_eb9312ecdde2fa2c50e199d4916d68e1d.png 180° 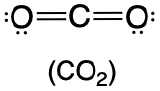clipboard_efb6914731f6cd38585e16eabce2edcd0.png
    3 trigonal plane 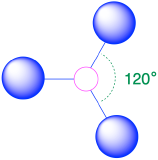clipboard_e3182b9b1c6d80b5ebdad2c66b73a2e6f.png 120° 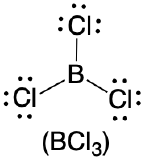clipboard_e8cf2169220755683f691f8b2cae5242f.png
    4 tetrahedron 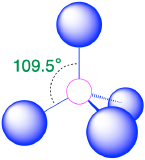clipboard_ea695c60caef5629399acfb59769cfa0e.png 109.5° 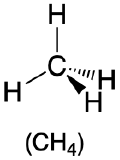clipboard_e8da1c4a1a3b8e70de878140e4f2c2817.png
    5 trigonal bipyramid 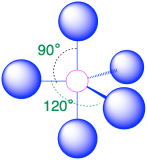clipboard_ee55b4f7ca03ee8477e1f5d6b204fd45b.png 90° and 120° 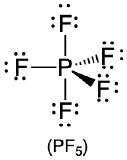clipboard_ed3acddc2a2a03fb6aa4c42074a7d5957.png
    6 octahedron 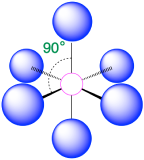clipboard_ea37bd90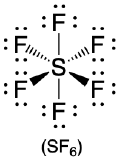86c0fb6b42452a9746fef9914.png 90° clipboard_e953f47ae566e30f4ea43ff7c8943aed7.png
    7 pentagonal bipyramid 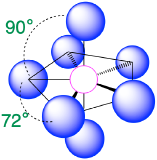clipboard_e35b713ebbc9ad70595fbe238e336c51e.png 90° and 72° clipboard_e6baf80619a2a2ba3cdc98bbf0a99a844.png
    8 square antiprism 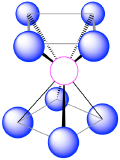clipboard_e7a25159fdfe4d982a4d39b00fd28fdf7.png 70.5°, 99.6° and 109.5° 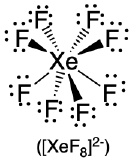clipboard_ed2d62e97b03a35a92d358896ff7d3104.png

    Practice

    VSEPR to predict Molecular Geometry

    You can follow these four steps to predict the geometry around an atom using VSEPR:

    1. Draw the Lewis electron structure of the molecule or polyatomic ion.
    2. For the central atom of interest, assign the AXmEn designation and the total number of groups (m+n).
    3. Determine the electron group arrangement around the central atom that minimizes repulsions.
    4. Describe the molecular geometry.

    Use the procedure above to complete the exercises below

    Exercise \(\PageIndex{1}\)

    Predict the geometry around the central atom in BeH2 and CO2.

    Answer BeH2

    1. The central atom, beryllium, contributes two valence electrons, and each hydrogen atom contributes one. The Lewis electron structure is

    imageedit_66_4595819201.png

    2. There are two groups around the central atom, and both groups are single bonds. Thus BeH2 is designated as AX2.

    3. We see from Table \(\PageIndex{1}\) that the arrangement that minimizes repulsions places the groups 180° apart.

    4. From Table \(\PageIndex{1}\) we see that with two bonding pairs, the molecular geometry that minimizes repulsions in BeH2 is linear.

    Answer CO2

    1. The central atom, carbon, contributes four valence electrons, and each oxygen atom contributes six. The Lewis electron structure is

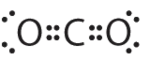
    imageedit_71_8792875617.png

    2. The carbon atom forms two double bonds. Each double bond is counted as one group, so there are two groups around the central atom. Once again, both groups around the central atom are bonds, so CO2 is designated as AX2.

    3. Like BeH2, the arrangement that minimizes repulsions places the groups 180° apart.

    4. VSEPR only recognizes groups around the central atom (the carbon). Thus the lone pairs on the oxygen atoms do not influence the molecular geometry. With two bonded groups on the central atom and no lone pairs, the molecular geometry of CO2 is linear (Table \(\PageIndex{1}\)). The structure of \(\ce{CO2}\) is shown in Table \(\PageIndex{1}\).

    Exercise \(\PageIndex{2}\)

    Predict the geometry around the central atom in BCl3 and CO32-.

    Answer BCl3

    1. The central atom, boron, contributes three valence electrons, and each chlorine atom contributes seven valence electrons. The Lewis electron structure is

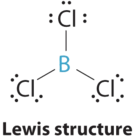
    imageedit_76_6350446108.png

    2. There are three groups around the central atom and all are single bonds. The structure is designated as AX3.

    3. To minimize repulsions, the groups are placed 120° apart (Table \(\PageIndex{1}\)).

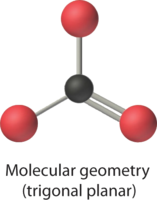
    4. From Table \(\PageIndex{1}\) we see that with three bonding pairs around the central atom, the molecular geometry of BCl3 is trigonal planar.

    Answer CO32-

    1. The central atom, carbon, has four valence electrons, and each oxygen atom has six valence electrons. The Lewis electron structure of one of three resonance forms is represented as

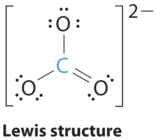
    imageedit_81_6956748295.png

    2. The structure of CO32− is a resonance hybrid. It has three identical bonds, each with a bond order of \(1 \frac{1}{3}\). All electron groups are bonds. With three bonding groups around the central atom, the structure is designated as AX3.

    3. We minimize repulsions by placing the three groups 120° apart (Table \(\PageIndex{1}\)).

    4. We see from Table \(\PageIndex{1}\) that the molecular geometry of CO32− is trigonal planar with bond angles of 120°.

    imageedit_86_9899847779.png

    In our next example we encounter the effects of lone pairs and multiple bonds on molecular geometry for the first time.

    Exercise \(\PageIndex{3}\)

    Predict the geometry around the central atom in CH4, PCl5 and SF6.

    Answer CH4

    1. The central atom, carbon, contributes four valence electrons, and each hydrogen atom has one valence electron, so the full Lewis electron structure is

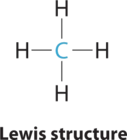
    imageedit_108_5449688695.png

    2. There are four electron groups around the central atom. All electron groups are bonding pairs, so the structure is designated as AX4.

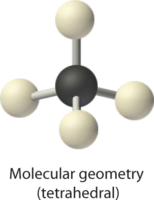
    3. As shown in Table \(\PageIndex{1}\), repulsions are minimized by placing the groups in the corners of a tetrahedron with bond angles of 109.5°.

    4. With four bonding pairs, the molecular geometry of methane is tetrahedral (Table \(\PageIndex{1}\)).

    imageedit_113_2836031615.png

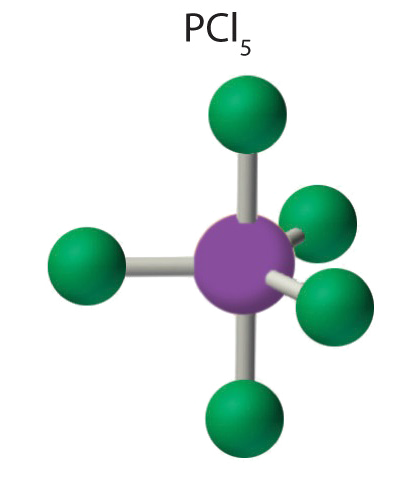
    Answer PCl5

    1. Phosphorus has five valence electrons and each chlorine has seven valence electrons, so the Lewis electron structure of PCl5 is

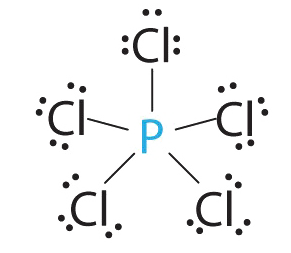
    9.2.1.png

    2. There are five bonding groups around phosphorus, the central atom. All electron groups are bonds, so the structure is designated as AX5.

    3. The structure that minimizes repulsions is a trigonal bipyramid, which consists of two trigonal pyramids that share a base (Table \(\PageIndex{1}\)).

    4. The molecular geometry of PCl5 is trigonal bipyramidal, as shown below. The molecule has three atoms in a plane in equatorial positions and two atoms above and below the plane in axial positions. The three equatorial positions are separated by 120° from one another, and the two axial positions are at 90° to the equatorial plane. The axial and equatorial positions are not chemically equivalent.

    9.2.2.png

    Answer SF6

    1. The central atom, sulfur, contributes six valence electrons, and each fluorine atom has seven valence electrons, so the Lewis electron structure is

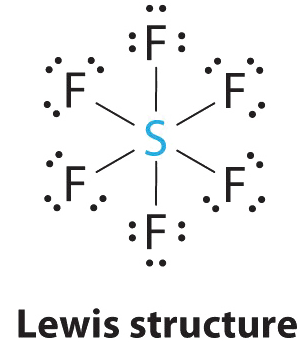
    9.2.11.png

    With an expanded valence, this species is an exception to the octet rule.

    2. There are six electron groups around the central atom, each a bonding pair. We see from Figure \(\PageIndex{2}\) that the geometry that minimizes repulsions is octahedral.

    3. With only bonding pairs, SF6 is designated as AX6. All positions are chemically equivalent, so all electronic interactions are equivalent.

    4. There are six nuclei, so the molecular geometry of SF6 is octahedral.

    9.2.12.png

    This page titled 3.2: Valence Shell Electron-Pair Repulsion is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Kathryn Haas.