27.2: Introduction to Substitution Reactions
- Page ID
- 24389
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In many ways, the proton transfer process in a Brønsted-Lowry acid-base reaction can be thought of as simply a special kind of nucleophilic substitution reaction, one in which the electrophile is a hydrogen rather than a carbon.
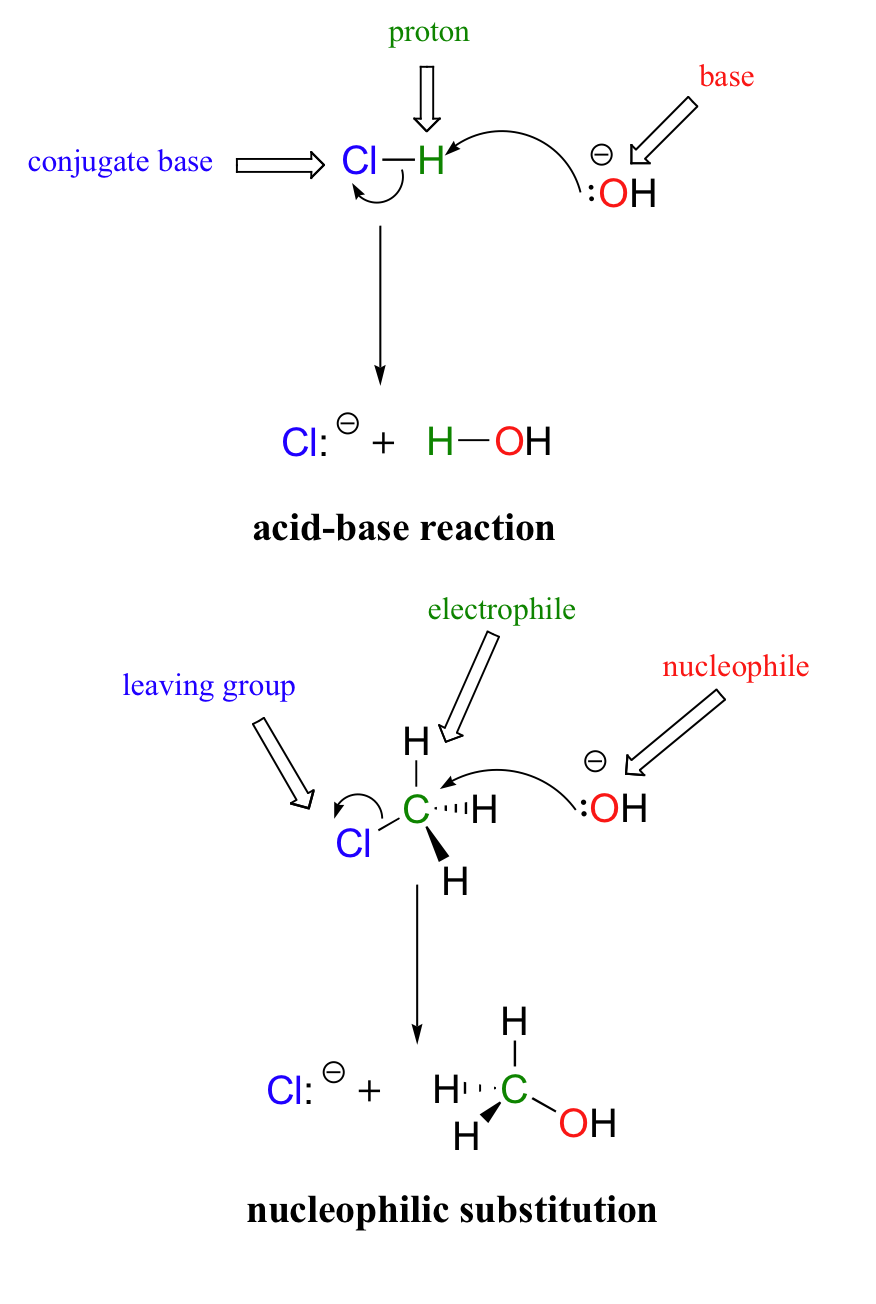
In both reaction types, we are looking at very similar players: an electron-rich species (the nucleophile/base) attacks an electron-poor species (the electrophile/proton), driving off the leaving group/conjugate base.In the next few sections, we are going to be discussing some general aspects of nucleophilic substitution reactions, and in doing so it will simplify things greatly if we can use some abbreviations and generalizations before we dive into real examples.
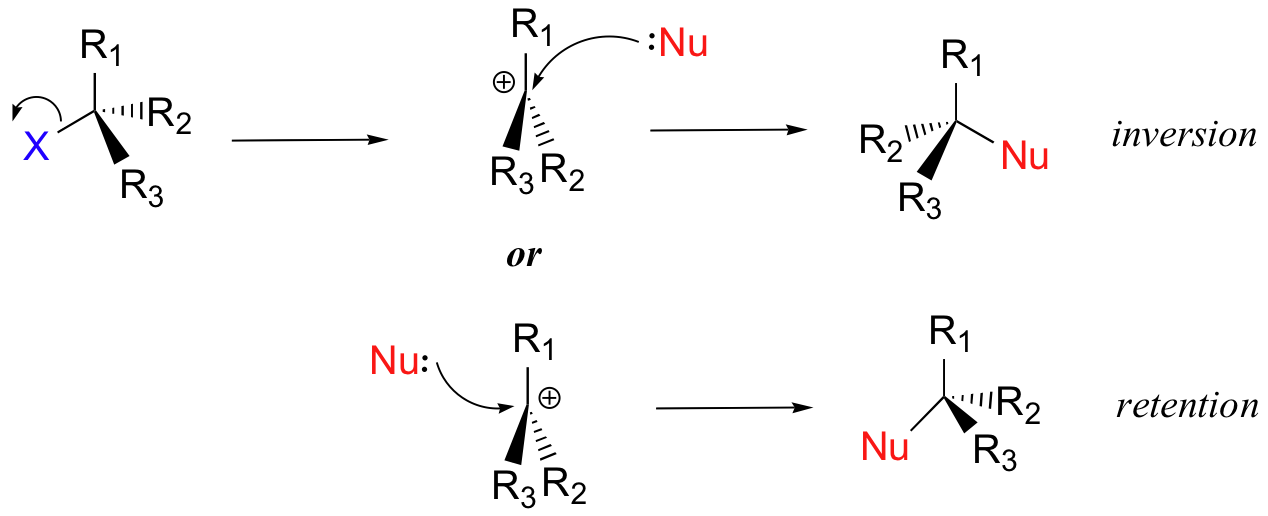
Instead of showing a specific nucleophile like hydroxide, we will simply refer to the nucleophilic reactant as 'Nu'. In a similar fashion, we will call the leaving group 'X'. We will see as we study actual reactions that leaving groups are sometimes negatively charged, sometimes neutral, and sometimes positively charged. We will also see some examples of nucleophiles that are negatively charged and some that are neutral. Therefore, in this general picture we will not include a charge designation on the 'X' or 'Nu' species. In the same way, we will see later that nucleophiles and leaving groups are sometimes protonated and sometimes not, so for now, for the sake of simplicity, we will not include protons on 'Nu' or 'X'. We will generalize the three other groups bonded on the electrophilic central carbon as R1, R2, and R3: these symbols could represent hydrogens as well as alkyl groups. Finally, in order to keep figures from becoming too crowded, we will use in most cases the line structure convention in which the central, electrophilic carbon is not drawn out as a 'C'.
Here, then, is the generalized picture of a concerted (single-step) nucleophilic substitution reaction:
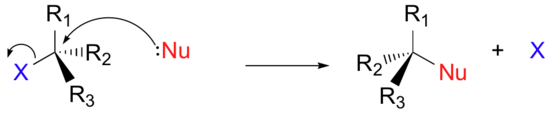
Associative nucleophilic substitution: the SN2 reaction
There are two mechanistic models for how a nucleophilic substitution reaction can proceed. In the first picture, the reaction takes place in a single step, and bond-forming and bond-breaking occur simultaneously.
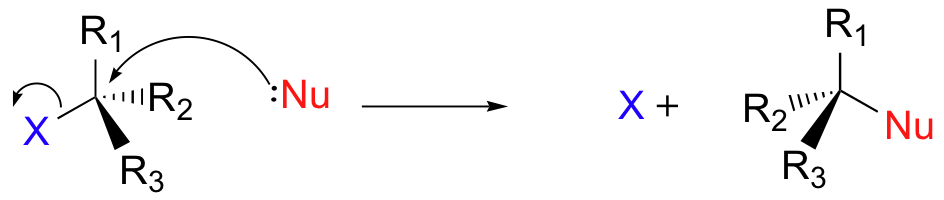
This is called an 'associative', or 'SN2' mechanism. In the term SN2, S stands for 'substitution', the subscript N stands for 'nucleophilic', and the number 2 refers to the fact that this is a bimolecular reaction: the overall rate depends on a step in which two separate molecules (the nucleophile and the electrophile) collide. A potential energy diagram for this reaction shows the transition state (TS) as the highest point on the pathway from reactants to products.

If you look carefully at the progress of the SN2 reaction, you will realize something very important about the outcome. The nucleophile, being an electron-rich species, must attack the electrophilic carbon from the back side relative to the location of the leaving group. Approach from the front side simply doesn't work: the leaving group - which is also an electron-rich group - blocks the way.

The result of this backside attack is that the stereochemical configuration at the central carbon inverts as the reaction proceeds. In a sense, the molecule is turned inside out. At the transition state, the electrophilic carbon and the three 'R' substituents all lie on the same plane.

What this means is that SN2 reactions whether enzyme catalyzed or not, are inherently stereoselective: when the substitution takes place at a stereocenter, we can confidently predict the stereochemical configuration of the product.
Dissociative nucleophilic substitution: the SN1 reaction
A second model for a nucleophilic substitution reaction is called the 'dissociative', or 'SN1' mechanism: in this picture, the C-X bond breaks first, before the nucleophile approaches:
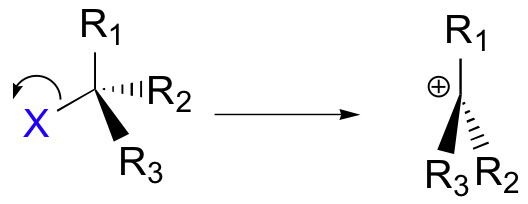
This results in the formation of a carbocation: because the central carbon has only three bonds, it bears a formal charge of +1. Recall that a carbocation should be pictured as sp2 hybridized, with trigonal planar geometry. Perpendicular to the plane formed by the three sp2 hybrid orbitals is an empty, unhybridized p orbital.

In the second step of this two-step reaction, the nucleophile attacks the empty, 'electron hungry' p orbital of the carbocation to form a new bond and return the carbon to tetrahedral geometry.
We saw that SN2 reactions result specifically in inversion of stereochemistry at the electrophilic carbon center. What about the stereochemical outcome of SN1 reactions? In the model SN1 reaction shown above, the leaving group dissociates completely from the vicinity of the reaction before the nucleophile begins its attack. Because the leaving group is no longer in the picture, the nucleophile is free to attack from either side of the planar, sp2-hybriduzed carbocation electrophile. This means that about half the time the product has the same stereochemical configuration as the starting material (retention of configuration), and about half the time the stereochemistry has been inverted. In other words, racemization has occurred at the carbon center. As an example, the tertiary alkyl bromide below would be expected to form a racemic mix of R and S alcohols after an SN1 reaction with water as the incoming nucleophile.

While most nonenzymatic SN1 reactions are not stereoselective, we will see later that enzyme-catalyzed nucleophilic substitution reactions - whether SN1 or SN2 - almost always are stereoselective. The direct result of an enzymatic nucleophilic substitution reaction is more often than not inversion of configuration - this is because the leaving group usually remains bound in the enzyme's active site long enough to block a nucleophilic attack from that side. This does not mean, however, that enzymes can only catalyze substitution reactions with inversion of configuration: we will see in the next chapter (section 9.2) an example of an enzymatic nucleophilic substitution reaction in which the overall result is 100% retention of configuration.
In the SN1 reaction we see an example of a reaction intermediate, a very important concept in the study of organic reaction mechanisms that was first introduced in Chapter 6. Recall that many important organic reactions do not occur in a single step; rather, they are the sum of two or more discreet bond-forming / bond-breaking steps, and involve transient intermediate species that go on to react very quickly. In the SN1 reaction, the carbocation species is a reaction intermediate. A potential energy diagram for an SN1 reaction shows that the carbocation intermediate can be visualized as a kind of valley in the path of the reaction, higher in energy than both the reactant and product but lower in energy than the two transition states.
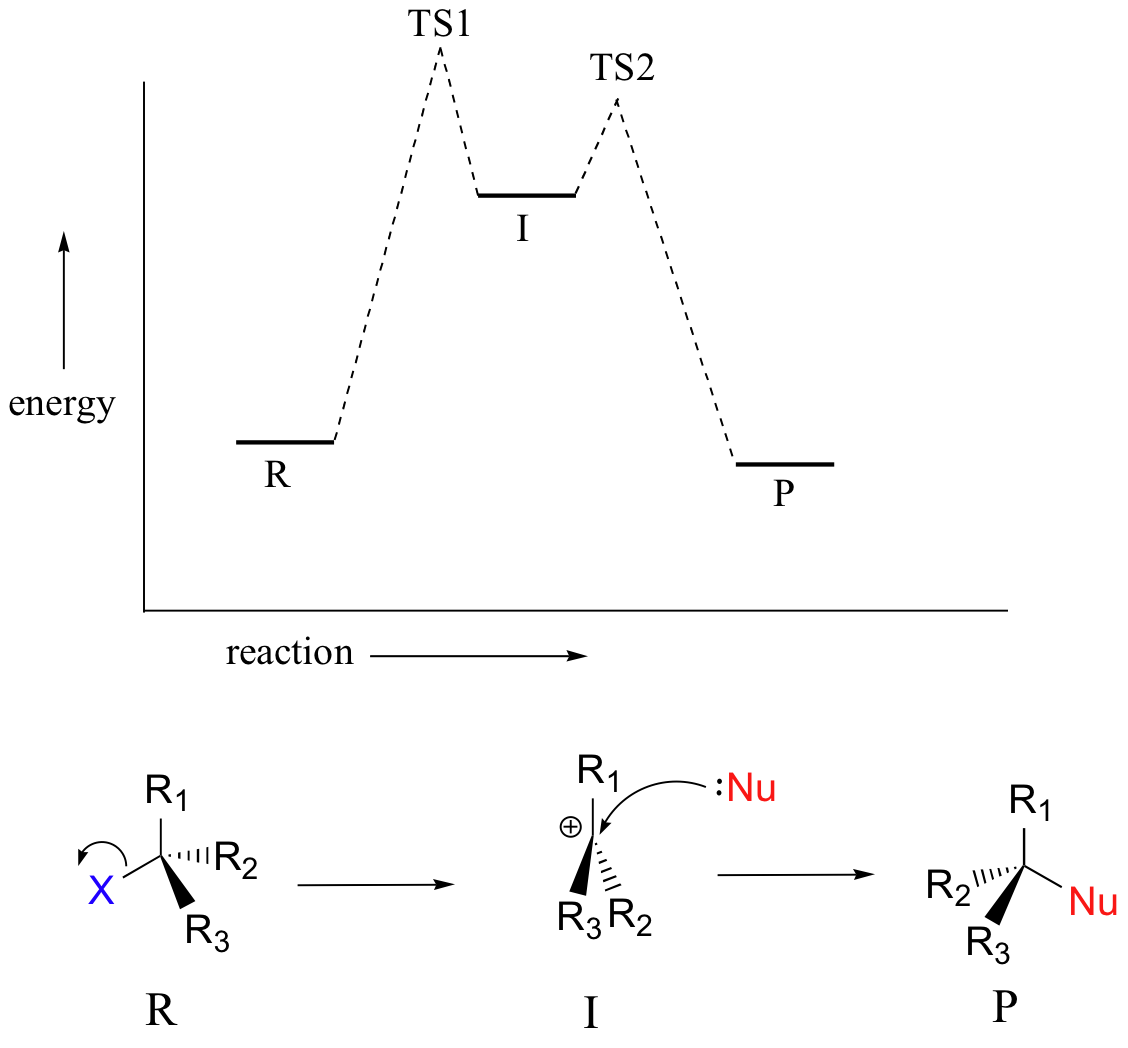
Recall (section 6.2) that the first step of the reaction above, in which two charged species are formed from a neutral molecule, is much the slower of the two steps, and is therefore rate-determining. This is illustrated by the energy diagram, where the activation energy for the first step is higher than that for the second step. Also recall that an SN1 reaction has first order kinetics, because the rate determining step involves one molecule splitting apart, not two molecules colliding.
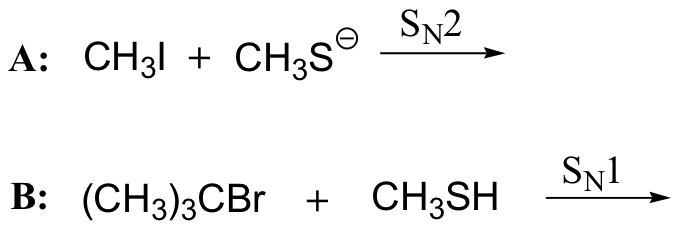
Consider two nucleophilic substitutions that occur uncatalyzed in solution. Assume that reaction A is SN2, and reaction B is SN1. Predict, in each case, what would happen to the rate of the reaction if the concentration of the nucleophile were doubled, while all other conditions remained constant.
Many SN1 reactions are of a class that are referred to as solvolysis, where a solvent molecule participates in the reaction as a nucleophile. The SN1 reaction of allyl bromide in methanol is an example of what we would call methanolysis, while if water is the solvent the reaction would be called hydrolysis:
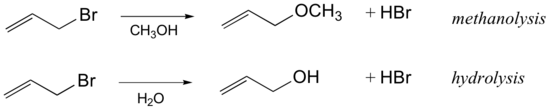
Because water and alcohols are relatively weak nucleophiles, they are unlikely to react in an SN2 fashion.
Nucleophilic substitutions occur at sp3-hybridized carbons
One more important point must be made before continuing: nucleophilic substitutions as a rule occur at sp3-hybridized carbons, and not where the leaving group is attached to an sp2-hybridized carbon::

Bonds on sp2-hybridized carbons are inherently shorter and stronger than bonds on sp3-hybridized carbons (section 1.5C), meaning that it is harder to break the C-X bond in these substrates. SN2 reactions of this type are unlikely also because the (hypothetical) electrophilic carbon is protected from nucleophilic attack by electron density in the p bond. SN1 reactions are highly unlikely, because the resulting carbocation intermediate, which would be sp-hybridized, would be very unstable (we’ll discuss the relative stability of carbocation intermediates in section 8.4B).
Before we look at some real-life nucleophilic substitution reactions in the next chapter, we will spend some time in the remainder of this chapter focusing more closely on the three principal partners in the nucleophilic substitution reaction: the nucleophile, the electrophile, and the leaving group.
What makes a nucleophile?
As a general rule, nucleophile substitution reactions that involve powerful nucleophiles tend to occur with SN2 mechanisms, while reactions with weaker nucleophiles tend to be SN1. But what makes a group a strong or weak nucleophile? Nucleophilic functional groups are those which have electron-rich atoms able to donate a pair of electrons to form a new covalent bond. In both laboratory and biological organic chemistry, the most relevant nucleophilic atoms are oxygen, nitrogen, and sulfur, and the most common nucleophilic functional groups are water, alcohols, phenols, amines, thiols, and occasionally carboxylates.
Of course, carbons can also be nucleophiles - otherwise how could new carbon-carbon bonds be formed in the synthesis of large organic molecules like DNA or fatty acids? When thinking about nucleophiles, the first thing to recognize is that, for the most part, the same quality of 'electron-richness' that makes a something nucleophilic also makes it basic: nucleophiles can be bases, and bases can be nucleophiles. It should not be surprising, then, that most of the trends in basicity that we have already discussed also apply to nucleophilicity.
Protonation states and nucleophilicity
The protonation state of a nucleophilic atom has a very large effect on its nucleophilicity. This is an idea that makes intuitive sense: a hydroxide ion is much more nucleophilic (and basic) than a water molecule, because the negatively charged oxygen on the hydroxide ion carries greater electron density than the oxygen atom of a neutral water molecule. In practical terms, this means that a hydroxide nucleophile will react in an SN2 reaction with methyl bromide much faster ( about 10,000 times faster) than a water nucleophile.
A neutral amine is nucleophilic, whereas a protonated ammonium cation is not. This is why enzymes which have evolved to catalyze nucleophilic reactions often have a basic amino acid side chain poised in position to accept a proton from the nucleophilic atom as the nucleophilic attack occurs.

Depending on the specific reaction being discussed, deprotonation of the nucleophile might occur before, during, or after the actual nucleophilic attack. In general for enzymatic reactions, however, it is most accurate to depict the proton abstraction and nucleophilic attack occurring simultaneously.
The basic enzymatic group could be a histidine, a neutral (deprotonated) arginine or lysine, or a negatively-charged (deprotonated) aspartate, glutamate, or tyrosine. For example, a more complete picture of the DNA methylation reaction we saw in section 8.1 shows an aspartate from the enzyme's active site accepting a proton from the nucleophilic amine as it attacks the carbon electrophile.
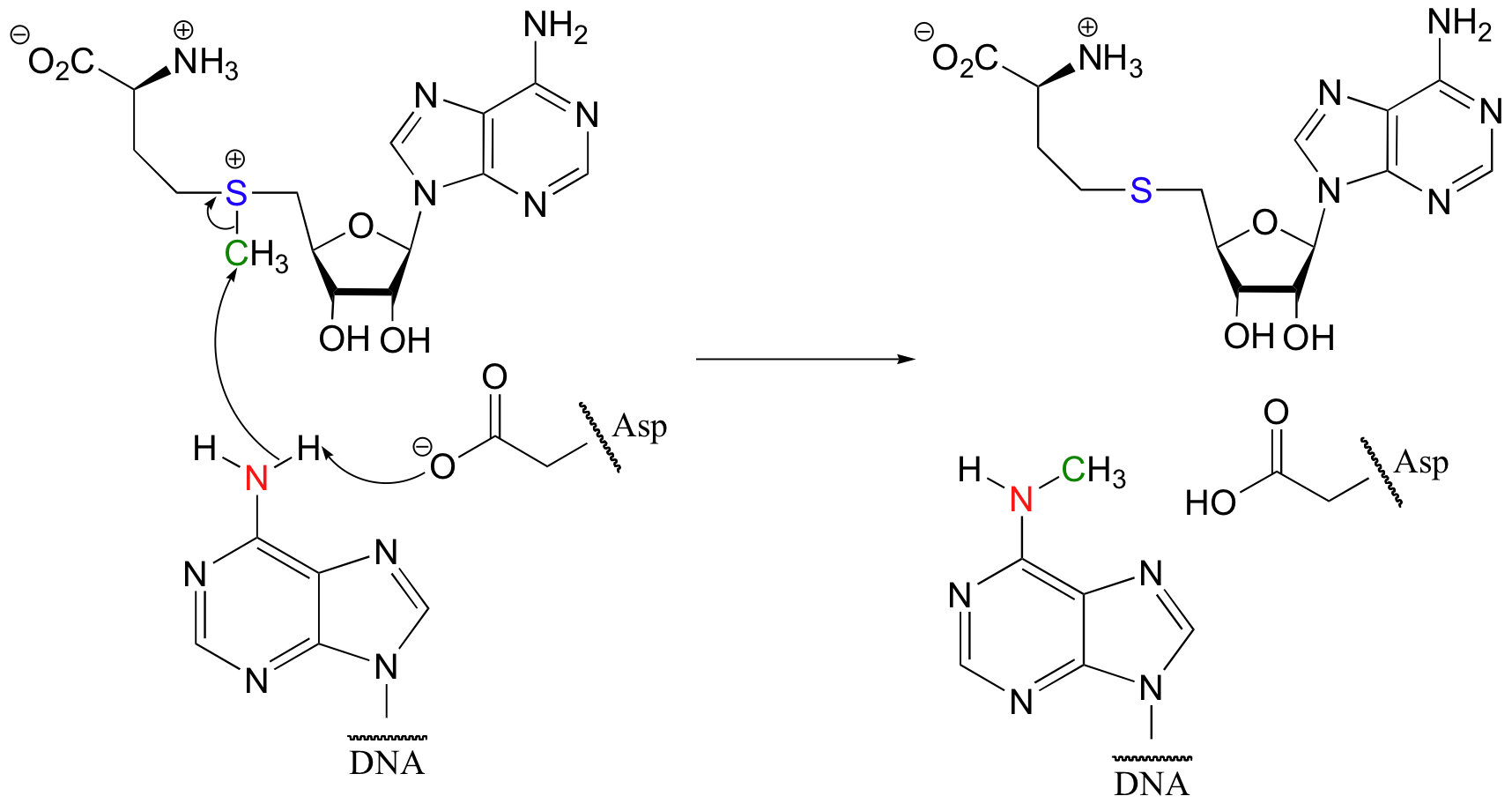
As it is deprotonated by the aspartate, the amine nitrogen becomes more electron-rich, and therefore more nucleophilic.
Periodic trends and solvent effects in nucleophilicity
There are predictable periodic trends in nucleophilicity. Moving horizontally across the second row of the table, the trend in nucleophilicity parallels the trend in basicity:
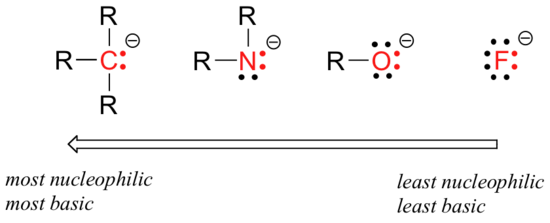
The reasoning behind the horizontal nucleophilicity trend is the same as the reasoning behind the basicity trend: more electronegative elements hold their electrons more tightly, and are less able to donate them to form a new bond. This horizontal trends also tells us that amines are more nucleophilic than alcohols, although both groups commonly act as nucleophiles in both laboratory and biochemical reactions.
Recall from section 7.3A that the basicity of atoms decreases as we move vertically down a column on the periodic table: thiolate ions are less basic than alkoxide ions, for example, and bromide ion is less basic than chloride ion, which in turn is less basic than fluoride ion. Recall also that this trend can be explained by considering the increasing size of the 'electron cloud' around the larger ions: the electron density inherent in the negative charge is spread around a larger area, which tends to increase stability (and thus reduce basicity).
The vertical periodic trend for nucleophilicity is somewhat more complicated that that for basicity: depending on the solvent that the reaction is taking place in, the nucleophilicity trend can go in either direction. Let's take the simple example of the SN2 reaction below:

. . .where Nu- is one of the halide ions: fluoride, chloride, bromide, or iodide, and the leaving group I* is a radioactive isotope of iodine (which allows us to distinguish the leaving group from the nucleophile in that case where both are iodide). If this reaction is occurring in a protic solvent (that is, a solvent that has a hydrogen bonded to an oxygen or nitrogen - water, methanol and ethanol are the most important examples), then the reaction will go fastest when iodide is the nucleophile, and slowest when fluoride is the nucleophile, reflecting the relative strength of the nucleophile.

This of course, is opposite that of the vertical periodic trend for basicity, where iodide is the least basic (you may want to review the reasoning for this trend in section 7.3A). What is going on here? Shouldn't the stronger base, with its more reactive unbonded valence electrons, also be the stronger nucleophile?
As mentioned above, it all has to do with the solvent. Remember, we are talking now about the reaction running in a protic solvent like ethanol. Protic solvent molecules form very strong ion-dipole interactions with the negatively-charged nucleophile, essentially creating a 'solvent cage' around the nucleophile:

In order for the nucleophile to attack the electrophile, it must break free, at least in part, from its solvent cage. The lone pair electrons on the larger, less basic iodide ion interact less tightly with the protons on the protic solvent molecules - thus the iodide nucleophile is better able to break free from its solvent cage compared the smaller, more basic fluoride ion, whose lone pair electrons are bound more tightly to the protons of the cage.
The picture changes if we switch to a polar aprotic solvent, such as acetone, in which there is a molecular dipole but no hydrogens bound to oxygen or nitrogen. Now, fluoride is the best nucleophile, and iodide the weakest.
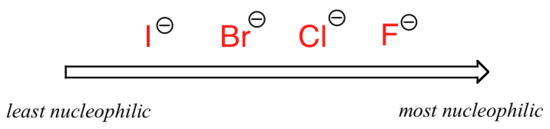
The reason for the reversal is that, with an aprotic solvent, the ion-dipole interactions between solvent and nucleophile are much weaker: the positive end of the solvent's dipole is hidden in the interior of the molecule, and thus it is shielded from the negative charge of the nucleophile.
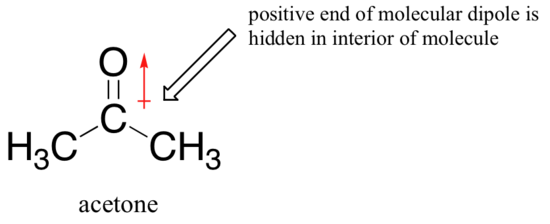
A weaker solvent-nucleophile interaction means a weaker solvent cage for the nucleophile to break through, so the solvent effect is much less important, and the more basic fluoride ion is also the better nucleophile.
Why not use a completely nonpolar solvent, such as hexane, for this reaction, so that the solvent cage is eliminated completely? The answer to this is simple - the nucleophile needs to be in solution in order to react at an appreciable rate with the electrophile, and a solvent such as hexane will not solvate an a charged (or highly polar) nucleophile at all. That is why chemists use polar aprotic solvents for nucleophilic substitution reactions in the laboratory: they are polar enough to solvate the nucleophile, but not so polar as to lock it away in an impenetrable solvent cage. In addition to acetone, three other commonly used polar aprotic solvents are acetonitrile, dimethylformamide (DMF), and dimethyl sulfoxide (DMSO).
In biological chemistry, where the solvent is protic (water), the most important implication of the periodic trends in nucleophilicity is that thiols are more powerful nucleophiles than alcohols. The thiol group in a cysteine amino acid, for example, is a powerful nucleophile and often acts as a nucleophile in enzymatic reactions, and of course negatively-charged thiolates (RS-) are even more nucleophilic. This is not to say that the hydroxyl groups on serine, threonine, and tyrosine do not also act as nucleophiles - they do.
Resonance effects on nucleophilicity
Resonance effects also come into play when comparing the inherent nucleophilicity of different molecules. The reasoning involved is the same as that which we used to understand resonance effects on basicity (see section 7.3C). If the electron lone pair on a heteroatom is delocalized by resonance, it is inherently less reactive - meaning less nucleophilic, and also less basic. An alkoxide ion, for example, is more nucleophilic and more basic than a carboxylate group, even though in both cases the nucleophilic atom is a negatively charged oxygen. In the alkoxide, the negative charge is localized on a single oxygen, while in the carboxylate the charge is delocalized over two oxygen atoms by resonance.

The nitrogen atom on an amide is less nucleophilic than the nitrogen of an amine, due to the resonance stabilization of the nitrogen lone pair provided by the amide carbonyl group.

Steric effects on nucleophilicity
Steric hindrance is an important consideration when evaluating nucleophility. For example, tert-butanol is less potent as a nucleophile than methanol. This is because the comparatively bulky methyl groups on the tertiary alcohol effectively block the route of attack by the nucleophilic oxygen, slowing the reaction down considerably (imagine trying to walk through a narrow doorway while carrying three large suitcases!).
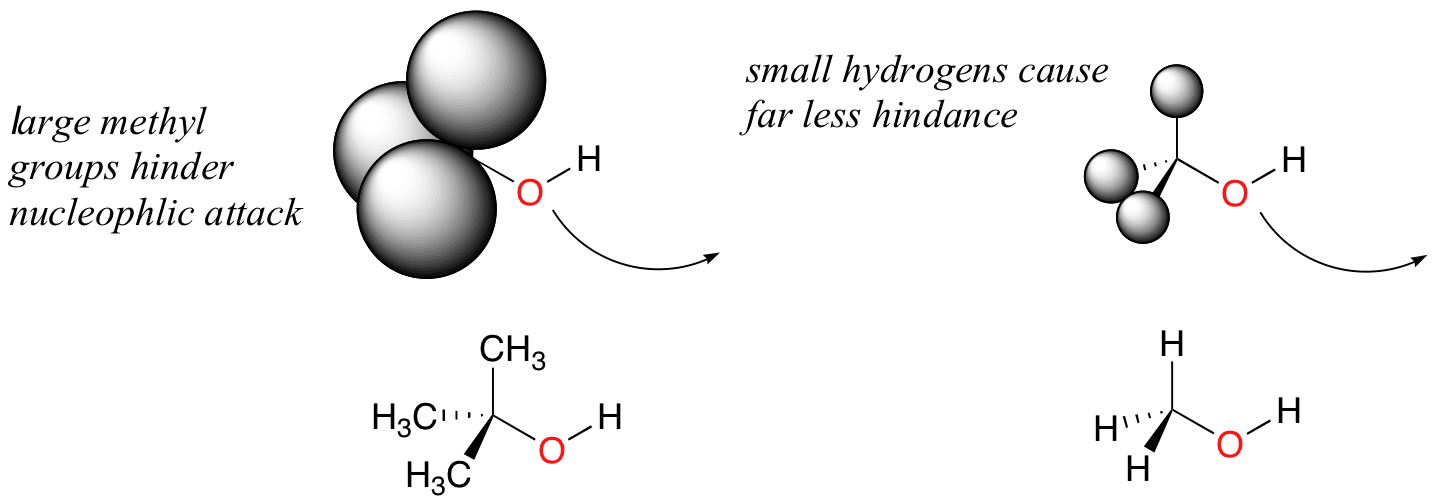
It is not surprising that it is more common to observe serines acting as nucleophiles in enzymatic reactions compared to threonines - the former is a primary alcohol, while the latter is a secondary alcohol.
Contributors and Attributions
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

