Electron Spin or Spin Quantum Number is the fourth quantum number for electrons in atoms and molecules. Denoted as \(m_s\), the electron spin is constituted by either upward (\(m_s=+1/2\)) or downward (\(m_s=-1/2\)) arrows.
Introduction
In 1920, Otto Stern and Walter Gerlach designed an experiment, which unintentionally led to the discovery that electrons have their own individual, continuous spin even as they move along their orbital of an atom. Today, this electron spin is indicated by the fourth quantum number, also known as the Electron Spin Quantum Number and denoted by ms. In 1925, Samuel Goudsmit and George Uhlenbeck made the claim that features of the hydrogen spectrum that were unexamined might by explained by assuming electrons act as if it has a spin. This spin can be denoted by an arrow pointing up, which is +1/2, or an arrow pointing down, which is -1/2.
The experiment mentioned above by Otto Stern and Walter Gerlach was done with silver which was put in an oven and vaporized. The result was that silver atoms formed a beam that passed through a magnetic field in which it split in two.
An explanation of this is that an electron has a magnetic field due to its spin. When electrons that have opposite spins are put together, there is no net magnetic field because the positive and negative spins cancel each other out. The silver atom used in the experiment has a total of 47 electrons, 23 of one spin type, and 24 of the opposite. Because electrons of the same spin cancel each other out, the one unpaired electron in the atom will determine the spin. There is a high likelihood for either spin due to the large number of electrons, so when it went through the magnetic field it split into two beams.
Brief Explanation of Quantum Numbers
Note: In this module, capital "L" will be used instead of small case "l" for angular momentum quantum number.
A total of four quantum numbers were developed to better understand the movement and pathway of electrons in its designated orbital within an atom.
- Principal quantum number (n): energy level n = 1, 2, 3, 4, ...
- Orbital Angular Momentum Quantum Number (L): shape (of orbital) L = 0, 1, 2, 3, ...n-1
- Magnetic Quantum Number (mL): orientation mL = interval of (-L, +L)
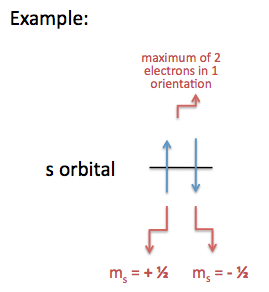
- Electron Spin Quantum Number (ms): independent of other three quantum numbers because ms is always = –½ or +½
(For more information about the three quantum numbers above, see Quantum Number.)

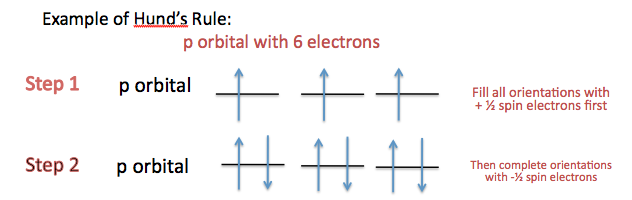
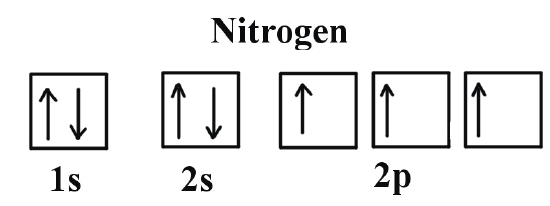
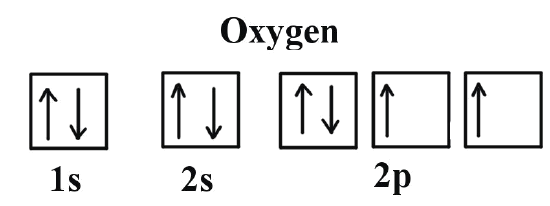
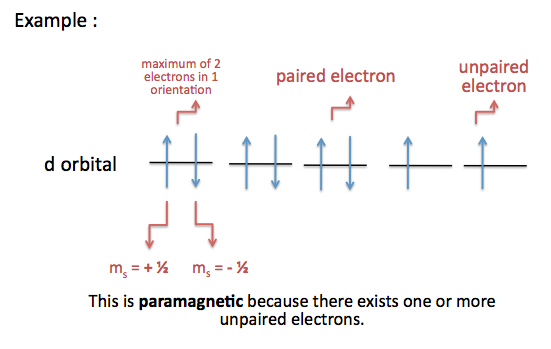
The lines represent how many orientations each orbital has, (e.g. the s-orbital has one orientation, a p-orbital has three orientations, etc.) and each line can hold up to two electrons, represented by up and down arrows. An electron with an up arrow means it has an electron spin of +\(\frac{1}{2}\), and an electron with a down arrow means it has an electron spin of -\(\frac{1}{2}\).
Electron Spin
Significance: determines if an atom will or will not generate a magnetic field (For more information, scroll down to Magnetic Spin, Magnetism, and Magnetic Field Lines). Although the electron spin is limited to +½ or –½, certain rules apply when assigning electrons of different spins to fill a subshell (orientations of an orbital) . For more information, scroll down to Assigning Spin Direction.
Solutions: Check your work!
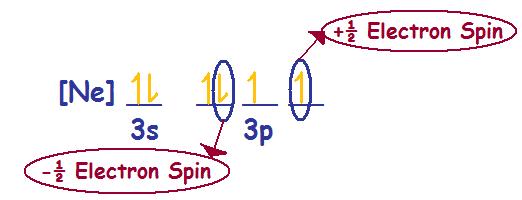
Problem (1): Sodium (Na) --> Electronic Configuration [Ne] 3s1

Spin direction for the valence electron or ms = +\(\frac{1}{2}\)
Sodium (Na) with a neutral charge of zero is paramagnetic, meaning that the electronic configuration for Na consists of one or more unpaired electrons.
Problem (2): Chlorine (Cl) --> Electronic Configuration [Ne] 3s2 3p5

Spin direction for the valence electron or ms = +\(\frac{1}{2}\)
Chlorine (Cl) with a neutral charge of zero is paramagnetic.
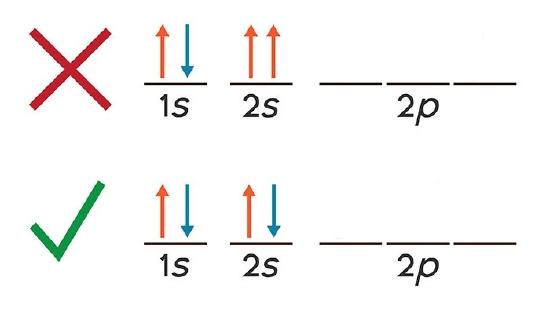
Problem (3): Calcium (Ca) --> Electronic Configuration [He] 4s2

Spin direction for the valence electron or ms = \(\pm\)\(\frac{1}{2}\)
Whereas for Calcium (Ca) with a neutral charge of zero, it is diamagnetic; meaning that ALL the electrons are paired as shown in the image above.
Problem (4): Given 5p and ms = -\(\frac{1}{2}\), identify all the possibilities of the four quantum numbers.
The principal quantum number is n = 5. Given that it is a p-orbital, we know that L = 1. And based on L, mL = 0, \(\pm\) 1 since mL = -L,...,-1, 0, 1,...+L. As for ms, this problem specifically says ms = -\(\frac{1}{2}\), meaning that the spin direction is -\(\frac{1}{2}\), pointing downwards ("down" spin).
Problem (5): Given 6f, identify all the possibilities of the four quantum numbers.
The principal quantum number is n = 6. Given that it is a f-orbital, we know that L = 3. Based on L, mL = 0, \(\pm\) 1, \(\pm\) 2, \(\pm\) 3 since mL = -L,...,-1, 0, 1,...+L. As for ms, since it isn't specified in the problem as to whether it is -\(\frac{1}{2}\) or +\(\frac{1}{2}\), therefore for this problem, it could be both; meaning that the electron spin quantum number is \(\pm\)\(\frac{1}{2}\).
Problem (6): How many electrons can have n = 4 and L = 1? 6
| n |
L |
mL |
ms |
| 4 |
1 |
\(\pm\) 1 |
-\(\frac{1}{2}\), + \(\frac{1}{2}\) |
| 0 |
This problem includes both -\(\frac{1}{2}\), +\(\frac{1}{2}\), therefore the answer is 6 electrons based on the mL.
Problem (7): How many electrons can have n = 4, L = 1, mL = -2 and ms = +\(\frac{1}{2}\)? zero
| n |
L |
mL |
ms |
| 4 |
1 |
NOT POSSIBLE |
+ \(\frac{1}{2}\) |
Since mL = -L...-1, 0, +1...+L, mL is not possible because L = 1, so it is impossible for mL to be equal to 2 when mL MUST be with the interval of -L and +L. So, there is zero electron.
Problem (8): How many electrons can have n = 5, L = 3, mL = \(\pm\) 2 and ms = +\(\frac{1}{2}\)? 2
| n |
L |
mL |
ms |
| 5 |
3 |
\(\pm\) 2 |
+ \(\frac{1}{2}\) |
| \(\pm\) 1 |
| 0 |
This problem only wants the Spin Quantum Number to be +\(\frac{1}{2}\) and mL = \(\pm\) 2, therefore 2 electrons can have n = 5, L = 3, mL = \(\pm\) 2 and ms = +\(\frac{1}{2}\).
Problem (9): How many electrons can have n = 5, L = 4 and mL = +3? 2
| n |
L |
mL |
ms |
| 5 |
4 |
-3, +3 |
-\(\frac{1}{2}\), + \(\frac{1}{2}\) |
| \(\pm\) 2 |
| \(\pm\) 1 |
| 0 |
This problem includes both -\(\frac{1}{2}\) and +\(\frac{1}{2}\) and given that mL = +3, therefore the answer is 2 electrons.
Problem (10): How many electrons can have n = 4, L = 2 and mL = \(\pm\) 1? 4
| n |
L |
mL |
ms |
| 4 |
2 |
\(\pm\) 1 |
-\(\frac{1}{2}\), + \(\frac{1}{2}\) |
| 0 |
This problem includes both -\(\frac{1}{2}\) and +\(\frac{1}{2}\) and given that mL = \(\pm\) 1, therefore the answer is 4 electrons.
Problem (11): How many electrons can have n = 3, L = 3, mL = +2 and ms = -\(\frac{1}{2}\)? zero
| n |
L |
mL |
ms |
| 3 |
3 (NOT POSSIBLE) |
\(\pm\) 2 |
-\(\frac{1}{2}\) |
| \(\pm\) 1 |
| 0 |
Since L = n - 1, there is zero electron, not possible because in this problem, n = L = 3.



.jpg?revision=1)