11.E: Liquids and Intermolecular Forces (Exercises)
- Page ID
- 24790
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)11.1: A Molecular Comparison of Gases, Liquids, and Solids
Q11.1.1
A liquid, unlike a gas, is virtually incompressible. Explain what this means using macroscopic and microscopic descriptions. What general physical properties do liquids share with solids? What properties do liquids share with gases?
Q11.1.2
Using a kinetic molecular approach, discuss the differences and similarities between liquids and gases with regard to
- thermal expansion.
- fluidity.
- diffusion.
Q11.1.3
How must the ideal gas law be altered to apply the kinetic molecular theory of gases to liquids? Explain.
Q11.1.4
Why are the root mean square speeds of molecules in liquids less than the root mean square speeds of molecules in gases?
11.2: Intermolecular Forces
Conceptual Problems
Q11.2.1
What is the main difference between intramolecular interactions and intermolecular interactions? Which is typically stronger? How are changes of state affected by these different kinds of interactions?
Q11.2.2
Describe the three major kinds of intermolecular interactions discussed in this chapter and their major features. The hydrogen bond is actually an example of one of the other two types of interaction. Identify the kind of interaction that includes hydrogen bonds and explain why hydrogen bonds fall into this category.
Q11.2.3
Which are stronger—dipole–dipole interactions or London dispersion forces? Which are likely to be more important in a molecule with heavy atoms? Explain your answers.
Q11.2.4
Explain why hydrogen bonds are unusually strong compared to other dipole–dipole interactions. How does the strength of hydrogen bonds compare with the strength of covalent bonds?
Q11.2.5
Liquid water is essential for life as we know it, but based on its molecular mass, water should be a gas under standard conditions. Why is water a liquid rather than a gas under standard conditions?
Q11.2.6
Describe the effect of polarity, molecular mass, and hydrogen bonding on the melting point and boiling point of a substance.
Q11.2.7
Why are intermolecular interactions more important for liquids and solids than for gases? Under what conditions must these interactions be considered for gases?
Q11.2.8
Using acetic acid as an example, illustrate both attractive and repulsive intermolecular interactions. How does the boiling point of a substance depend on the magnitude of the repulsive intermolecular interactions?
Q11.2.9
In group 17, elemental fluorine and chlorine are gases, whereas bromine is a liquid and iodine is a solid. Why?
Q11.2.10
The boiling points of the anhydrous hydrogen halides are as follows: HF, 19°C; HCl, −85°C; HBr, −67°C; and HI, −34°C. Explain any trends in the data, as well as any deviations from that trend.
Q11.2.11
Identify the most important intermolecular interaction in each of the following.
- SO2
- HF
- CO2
- CCl4
- CH2Cl2
Q11.2.12
Identify the most important intermolecular interaction in each of the following.
- LiF
- I2
- ICl
- NH3
- NH2Cl
Q11.2.13
Would you expect London dispersion forces to be more important for Xe or Ne? Why? (The atomic radius of Ne is 38 pm, whereas that of Xe is 108 pm.)
Q11.2.14
Arrange Kr, Cl2, H2, N2, Ne, and O2 in order of increasing polarizability. Explain your reasoning.
Q11.2.15
Both water and methanol have anomalously high boiling points due to hydrogen bonding, but the boiling point of water is greater than that of methanol despite its lower molecular mass. Why? Draw the structures of these two compounds, including any lone pairs, and indicate potential hydrogen bonds.
Q11.2.16
The structures of ethanol, ethylene glycol, and glycerin are as follows:
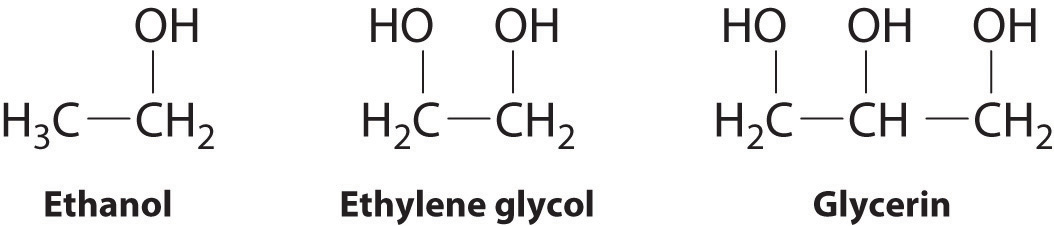
Arrange these compounds in order of increasing boiling point. Explain your rationale.
Q11.2.17
Do you expect the boiling point of H2S to be higher or lower than that of H2O? Justify your answer.
Q11.2.18
Ammonia (NH3), methylamine (CH3NH2), and ethylamine (CH3CH2NH2) are gases at room temperature, while propylamine (CH3CH2CH2NH2) is a liquid at room temperature. Explain these observations.
Q11.2.19
Why is it not advisable to freeze a sealed glass bottle that is completely filled with water? Use both macroscopic and microscopic models to explain your answer. Is a similar consideration required for a bottle containing pure ethanol? Why or why not?
Q11.2.20
Which compound in the following pairs will have the higher boiling point? Explain your reasoning.
- NH3 or PH3
- ethylene glycol (HOCH2CH2OH) or ethanol
- 2,2-dimethylpropanol [CH3C(CH3)2CH2OH] or n-butanol (CH3CH2CH2CH2OH)
Q11.2.21
Some recipes call for vigorous boiling, while others call for gentle simmering. What is the difference in the temperature of the cooking liquid between boiling and simmering? What is the difference in energy input?
Q11.2.22
Use the melting of a metal such as lead to explain the process of melting in terms of what is happening at the molecular level. As a piece of lead melts, the temperature of the metal remains constant, even though energy is being added continuously. Why?
Q11.2.23
How does the O–H distance in a hydrogen bond in liquid water compare with the O–H distance in the covalent O–H bond in the H2O molecule? What effect does this have on the structure and density of ice?
Q11.2.24
Explain why the hydrogen bonds in liquid HF are stronger than the corresponding intermolecular H⋅⋅⋅I interactions in liquid HI.
- In which substance are the individual hydrogen bonds stronger: HF or H2O? Explain your reasoning.
- For which substance will hydrogen bonding have the greater effect on the boiling point: HF or H2O? Explain your reasoning.
Answers
-
-
-
-
-
Water is a liquid under standard conditions because of its unique ability to form four strong hydrogen bonds per molecule.
-
-
-
-
As the atomic mass of the halogens increases, so does the number of electrons and the average distance of those electrons from the nucleus. Larger atoms with more electrons are more easily polarized than smaller atoms, and the increase in polarizability with atomic number increases the strength of London dispersion forces. These intermolecular interactions are strong enough to favor the condensed states for bromine and iodine under normal conditions of temperature and pressure.
-
-
- The V-shaped SO2 molecule has a large dipole moment due to the polar S=O bonds, so dipole–dipole interactions will be most important.
- The H–F bond is highly polar, and the fluorine atom has three lone pairs of electrons to act as hydrogen bond acceptors; hydrogen bonding will be most important.
- Although the C=O bonds are polar, this linear molecule has no net dipole moment; hence, London dispersion forces are most important.
- This is a symmetrical molecule that has no net dipole moment, and the Cl atoms are relatively polarizable; thus, London dispersion forces will dominate.
- This molecule has a small dipole moment, as well as polarizable Cl atoms. In such a case, dipole–dipole interactions and London dispersion forces are often comparable in magnitude.
-
-
-
-
Water has two polar O–H bonds with H atoms that can act as hydrogen bond donors, plus two lone pairs of electrons that can act as hydrogen bond acceptors, giving a net of four hydrogen bonds per H2O molecule. Although methanol also has two lone pairs of electrons on oxygen that can act as hydrogen bond acceptors, it only has one O–H bond with an H atom that can act as a hydrogen bond donor. Consequently, methanol can only form two hydrogen bonds per molecule on average, versus four for water. Hydrogen bonding therefore has a much greater effect on the boiling point of water.
-
-
-
-
-
-
Vigorous boiling causes more water molecule to escape into the vapor phase, but does not affect the temperature of the liquid. Vigorous boiling requires a higher energy input than does gentle simmering.
11.3: Some Properties of Liquids
Conceptual Problems
-
Why is a water droplet round?
-
How is the environment of molecules on the surface of a liquid droplet different from that of molecules in the interior of the droplet? How is this difference related to the concept of surface tension?
-
Explain the role of intermolecular and intramolecular forces in surface tension.
-
A mosquito is able to walk across water without sinking, but if a few drops of detergent are added to the water, the insect will sink. Why?
-
Explain how soaps or surfactants decrease the surface tension of a liquid. How does the meniscus of an aqueous solution in a capillary change if a surfactant is added? Illustrate your answer with a diagram.
-
Of CH2Cl2, hexane, and ethanol, which has the lowest viscosity? Which has the highest surface tension? Explain your reasoning in each case.
-
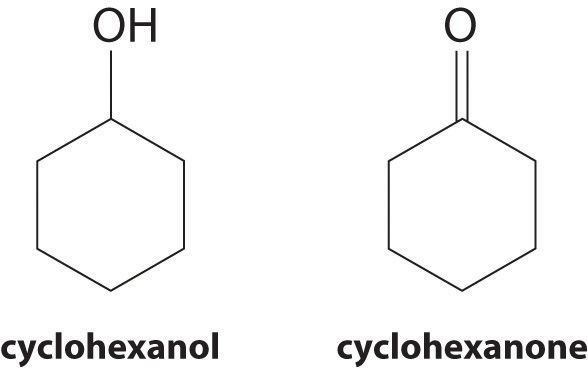
At 25°C, cyclohexanol has a surface tension of 32.92 mN/m2, whereas the surface tension of cyclohexanone, which is very similar chemically, is only 25.45 mN/m2. Why is the surface tension of cyclohexanone so much less than that of cyclohexanol?
-
What is the relationship between
- surface tension and temperature?
- viscosity and temperature?
Explain your answers in terms of a microscopic picture.
-
What two opposing forces are responsible for capillary action? How do these forces determine the shape of the meniscus?
-
Which of the following liquids will have a concave meniscus in a glass capillary? Explain your reasoning.
- pentane
- diethylene glycol (HOCH2CH2OCH2CH2OH)
- carbon tetrachloride
-
How does viscosity depend on molecular shape? What molecular features make liquids highly viscous?
Conceptual Answers
-
-
-
-
-
Adding a soap or a surfactant to water disrupts the attractive intermolecular interactions between water molecules, thereby decreasing the surface tension. Because water is a polar molecule, one would expect that a soap or a surfactant would also disrupt the attractive interactions responsible for adhesion of water to the surface of a glass capillary. As shown in the sketch, this would decrease the height of the water column inside the capillary, as well as making the meniscus less concave.

-
-
As the structures indicate, cyclohexanol is a polar substance that can engage in hydrogen bonding, much like methanol or ethanol; consequently, it is expected to have a higher surface tension due to stronger intermolecular interactions.
-
-
Cohesive forces are the intermolecular forces that hold the molecules of the liquid together, while adhesive forces are the attractive forces between the molecules of the liquid and the walls of the capillary. If the adhesive forces are stronger than the cohesive forces, the liquid is pulled up into the capillary and the meniscus is concave. Conversely, if the cohesive forces are stronger than the adhesive forces, the level of the liquid inside the capillary will be lower than the level outside the capillary, and the meniscus will be convex.
-
-
Viscous substances often consist of molecules that are much longer than they are wide and whose structures are often rather flexible. As a result, the molecules tend to become tangled with one another (much like overcooked spaghetti), which decreases the rate at which they can move through the liquid.
Numerical Problems
-
The viscosities of five liquids at 25°C are given in the following table. Explain the observed trends in viscosity.
Compound Molecular Formula Viscosity (mPa•s) benzene C6H6 0.604 aniline C6H5NH2 3.847 1,2-dichloroethane C2H4Cl2 0.779 heptane C7H16 0.357 1-heptanol C7H15OH 5.810
-
The following table gives values for the viscosity, boiling point, and surface tension of four substances. Examine these data carefully to see whether the data for each compound are internally consistent and point out any obvious errors or inconsistencies. Explain your reasoning.
Compound Viscosity (mPa•s at 20°C) Boiling Point (°C) Surface Tension (dyn/cm at 25°C) A 0.41 61 27.16 B 0.55 65 22.55 C 0.92 105 36.76 D 0.59 110 28.53 -
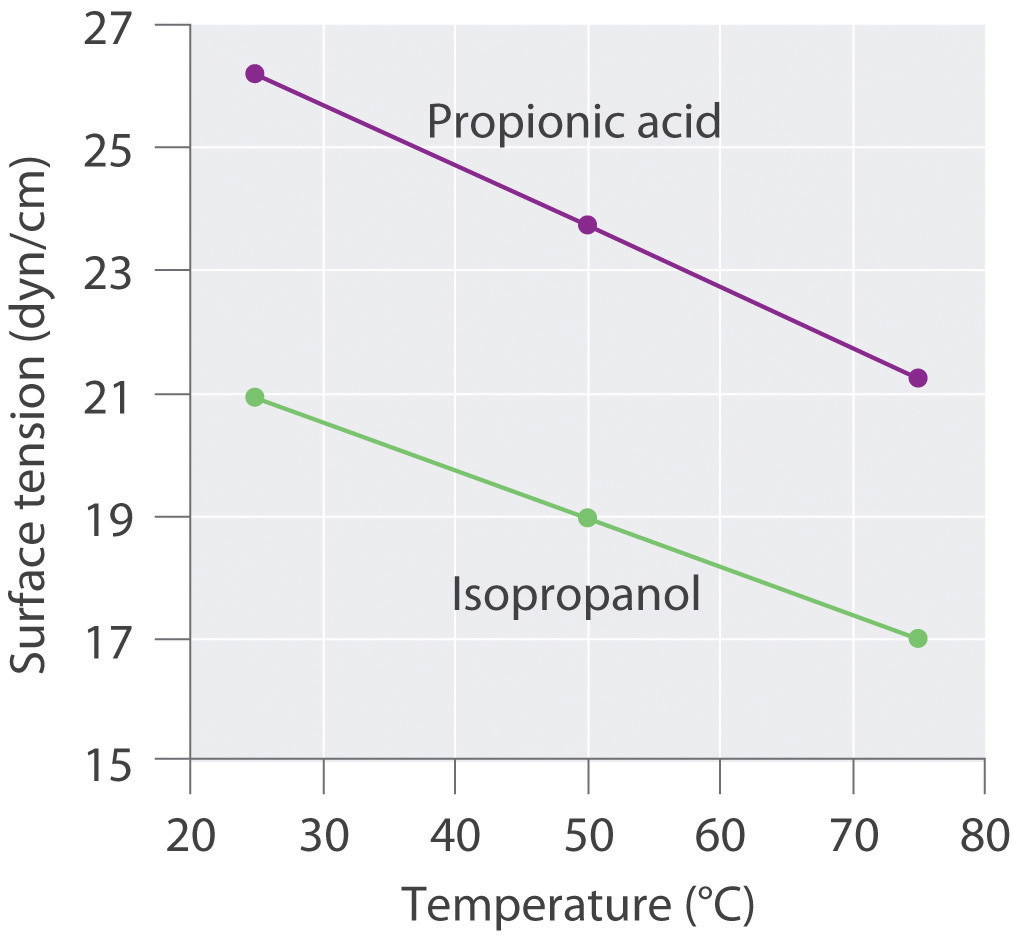
Surface tension data (in dyn/cm) for propanoic acid (C3H6O2), and 2-propanol (C3H8O), as a function of temperature, are given in the following table. Plot the data for each compound and explain the differences between the two graphs. Based on these data, which molecule is more polar?
Compound 25°C 50°C 75°C propanoic acid 26.20 23.72 21.23 2-propanol 20.93 18.96 16.98
Numerical Answer
3. The plots of surface tension versus temperature for propionic acid and isopropanol have essentially the same slope, but at all temperatures the surface tension of propionic acid is about 30% greater than for isopropanol. Because surface tension is a measure of the cohesive forces in a liquid, these data suggest that the cohesive forces for propionic acid are significantly greater than for isopropanol. Both substances consist of polar molecules with similar molecular masses, and the most important intermolecular interactions are likely to be dipole–dipole interactions. Consequently, these data suggest that propionic acid is more polar than isopropanol.
11.4: Phase Changes
Conceptual Problems
-
In extremely cold climates, snow can disappear with no evidence of its melting. How can this happen? What change(s) in state are taking place? Would you expect this phenomenon to be more common at high or low altitudes? Explain your answer.
-
Why do car manufacturers recommend that an automobile should not be left standing in subzero temperatures if its radiator contains only water? Car manufacturers also warn car owners that they should check the fluid level in a radiator only when the engine is cool. What is the basis for this warning? What is likely to happen if it is ignored?
-
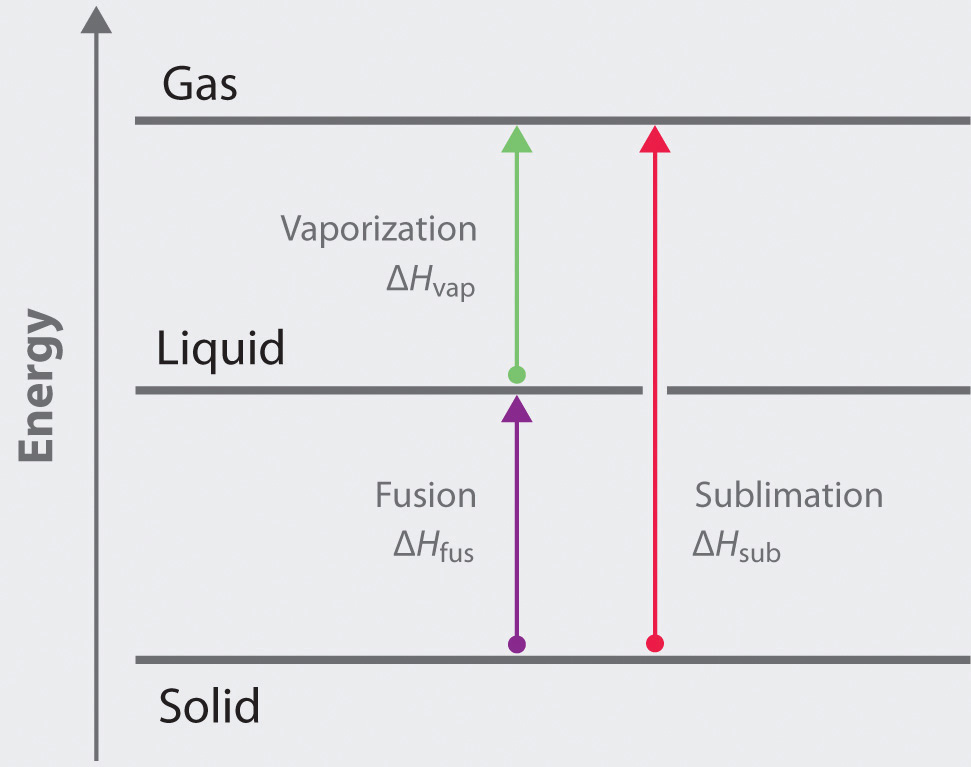
Use Hess’s law and a thermochemical cycle to show that, for any solid, the enthalpy of sublimation is equal to the sum of the enthalpy of fusion of the solid and the enthalpy of vaporization of the resulting liquid.
-
Three distinct processes occur when an ice cube at −10°C is used to cool a glass of water at 20°C. What are they? Which causes the greatest temperature change in the water?
-
When frost forms on a piece of glass, crystals of ice are deposited from water vapor in the air. How is this process related to sublimation? Describe the energy changes that take place as the water vapor is converted to frost.
-
What phase changes are involved in each process? Which processes are exothermic, and which are endothermic?
- ice melting
- distillation
- condensation forming on a window
- the use of dry ice to create a cloud for a theatrical production
-
What phase changes are involved in each process? Which processes are exothermic, and which are endothermic?
- evaporation of methanol
- crystallization
- liquefaction of natural gas
- the use of naphthalene crystals to repel moths
-
Why do substances with high enthalpies of fusion tend to have high melting points?
-
Why is the enthalpy of vaporization of a compound invariably much larger than its enthalpy of fusion?
-
What is the opposite of fusion, sublimation, and condensation? Describe the phase change in each pair of opposing processes and state whether each phase change is exothermic or endothermic.
-
Draw a typical heating curve (temperature versus amount of heat added at a constant rate) for conversion of a solid to a liquid and then to a gas. What causes some regions of the plot to have a positive slope? What is happening in the regions of the plot where the curve is horizontal, meaning that the temperature does not change even though heat is being added?
-
If you know the mass of a sample of a substance, how could you use a heating curve to calculate the specific heat of the substance, as well as the change in enthalpy associated with a phase change?
-
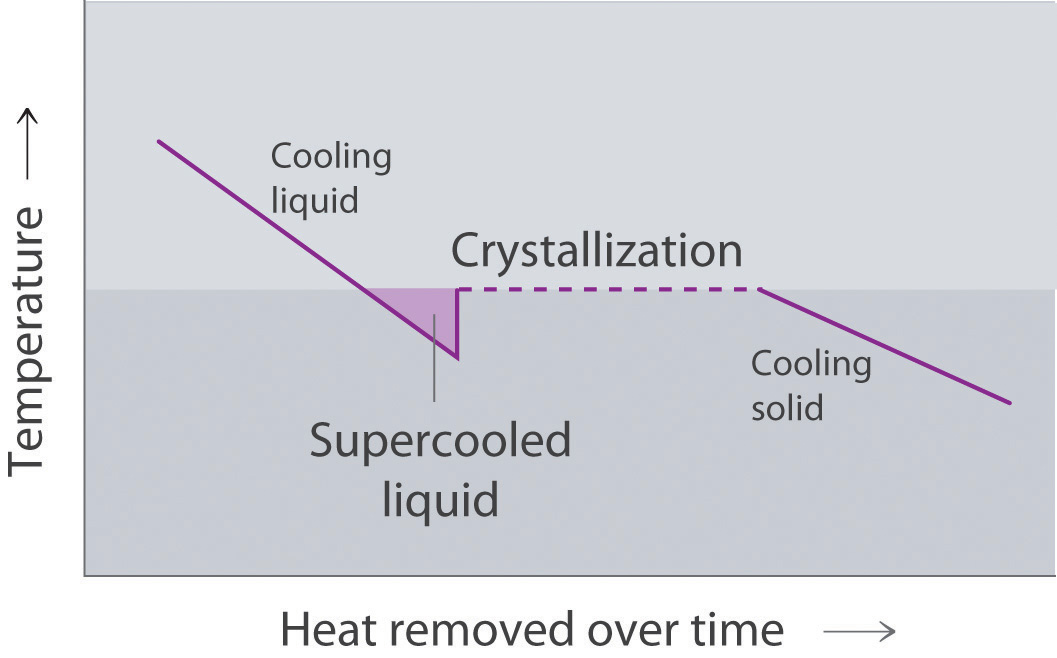
Draw the heating curve for a liquid that has been superheated. How does this differ from a normal heating curve for a liquid? Draw the cooling curve for a liquid that has been supercooled. How does this differ from a normal cooling curve for a liquid?
Conceptual Answers
-
When snow disappears without melting, it must be subliming directly from the solid state to the vapor state. The rate at which this will occur depends solely on the partial pressure of water, not on the total pressure due to other gases. Consequently, altitude (and changes in atmospheric pressure) will not affect the rate of sublimation directly.
-
3 The general equations and enthalpy changes for the changes of state involved in converting a solid to a gas are:
\[ \text{solid} \rightarrow \text{liquid}: \Delta H_{fus} \]
\[ \text{liquid} \rightarrow \text{gas}: \Delta H_{vap} \]
\[ \text{solid} \rightarrow \text{gas}: \Delta{H_{sub}}= \Delta{H_{fus}} + \Delta{H_{vap}}\]
The relationship between these enthalpy changes is shown schematically in the thermochemical cycle below:
-
-
The formation of frost on a surface is an example of deposition, which is the reverse of sublimation. The change in enthalpy for deposition is equal in magnitude, but opposite in sign, to ΔHsub, which is a positive number: ΔHsub = ΔHfus + ΔHvap.
-
-
- liquid + heat → vapor: endothermic
- liquid → solid + heat: exothermic
- gas → liquid + heat: exothermic
- solid + heat → vapor: endothermic
-
-
The enthalpy of vaporization is larger than the enthalpy of fusion because vaporization requires the addition of enough energy to disrupt all intermolecular interactions and create a gas in which the molecules move essentially independently. In contrast, fusion requires much less energy, because the intermolecular interactions in a liquid and a solid are similar in magnitude in all condensed phases. Fusion requires only enough energy to overcome the intermolecular interactions that lock molecules in place in a lattice, thereby allowing them to move more freely.
-
-
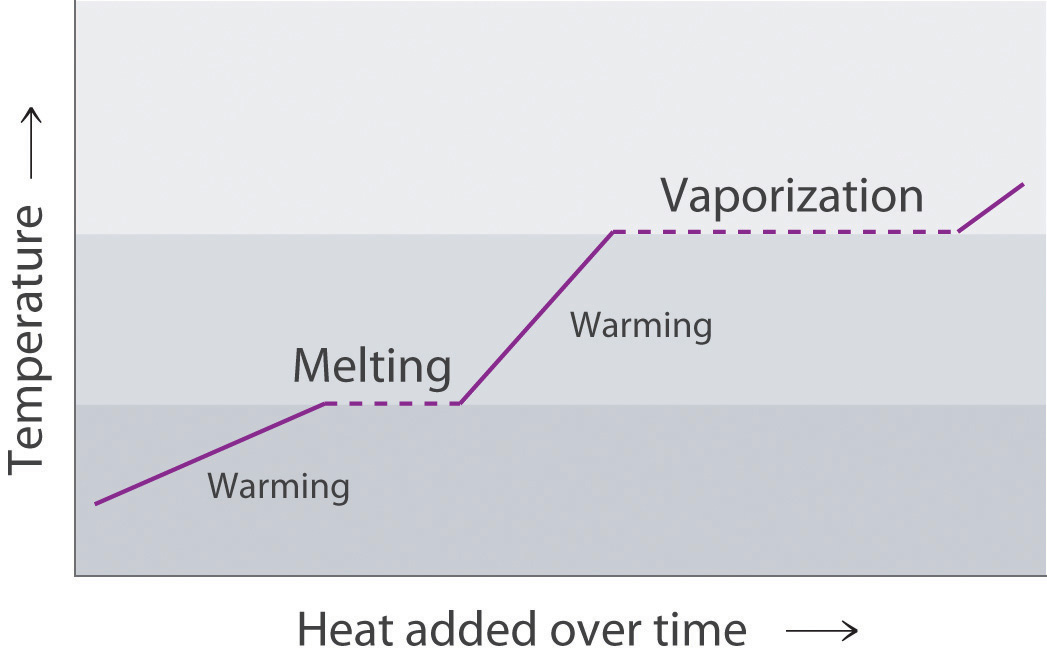
The portions of the curve with a positive slope correspond to heating a single phase, while the horizontal portions of the curve correspond to phase changes. During a phase change, the temperature of the system does not change, because the added heat is melting the solid at its melting point or evaporating the liquid at its boiling point.
-
-
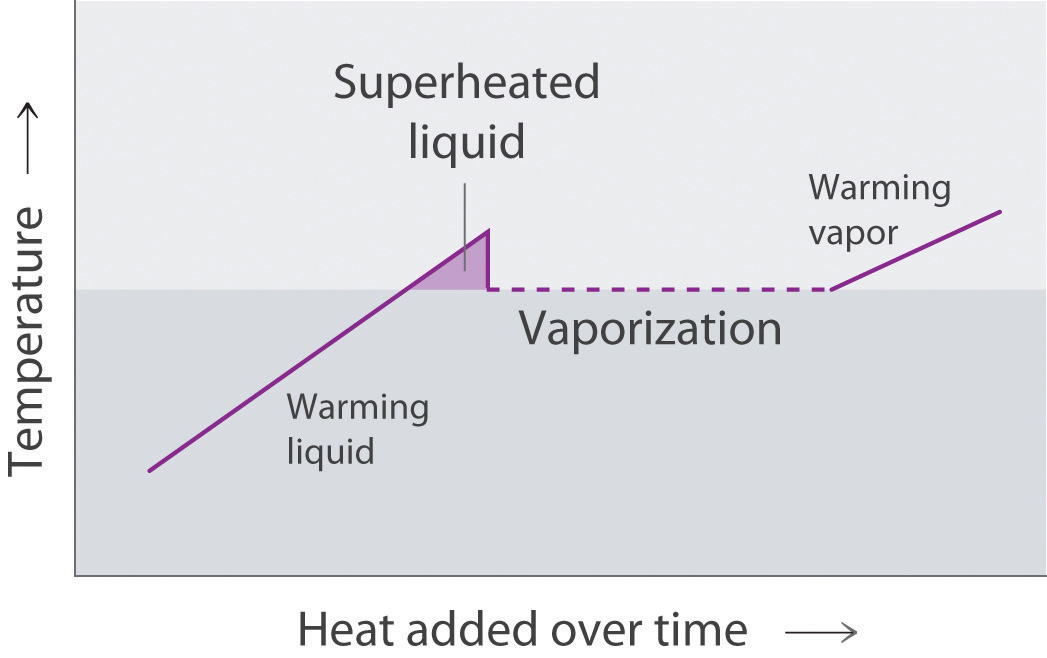
A superheated liquid exists temporarily as liquid with a temperature above the normal boiling point of the liquid. When a supercooled liquid boils, the temperature drops as the liquid is converted to vapor.
Conversely, a supercooled liquid exists temporarily as a liquid with a temperature lower than the normal melting point of the solid. As shown below, when a supercooled liquid crystallizes, the temperature increases as the liquid is converted to a solid.
Numerical Problems
-
The density of oxygen at 1 atm and various temperatures is given in the following table. Plot the data and use your graph to predict the normal boiling point of oxygen.
T (K) 60 70 80 90 100 120 140 d (mol/L) 40.1 38.6 37.2 35.6 0.123 0.102 0.087 -
The density of propane at 1 atm and various temperatures is given in the following table. Plot the data and use your graph to predict the normal boiling point of propane.
T (K) 100 125 150 175 200 225 250 275 d (mol/L) 16.3 15.7 15.0 14.4 13.8 13.2 0.049 0.044
-
Draw the cooling curve for a sample of the vapor of a compound that has a melting point of 34°C and a boiling point of 77°C as it is cooled from 100°C to 0°C.
-
Propionic acid has a melting point of −20.8°C and a boiling point of 141°C. Draw a heating curve showing the temperature versus time as heat is added at a constant rate to show the behavior of a sample of propionic acid as it is heated from −50°C to its boiling point. What happens above 141°C?
-
A 0.542 g sample of I2 requires 96.1 J of energy to be converted to vapor. What is the enthalpy of sublimation of I2?
-
A 2.0 L sample of gas at 210°C and 0.762 atm condenses to give 1.20 mL of liquid, and 476 J of heat is released during the process. What is the enthalpy of vaporization of the compound?
-
One fuel used for jet engines and rockets is aluminum borohydride [Al(BH4)3], a liquid that readily reacts with water to produce hydrogen. The liquid has a boiling point of 44.5°C. How much energy is needed to vaporize 1.0 kg of aluminum borohydride at 20°C, given a ΔHvap of 30 kJ/mol and a molar heat capacity (Cp) of 194.6 J/(mol•K)?
-
How much energy is released when freezing 100.0 g of dimethyl disulfide (C2H6S2) initially at 20°C? Use the following information: melting point = −84.7°C, ΔHfus = 9.19 kJ/mol, Cp = 118.1 J/(mol•K).
The following four problems use the following information (the subscript p indicates measurements taken at constant pressure): ΔHfus(H2O) = 6.01 kJ/mol, ΔHvap(H2O) = 40.66 kJ/mol, Cp(s)(crystalline H2O) = 38.02 J/(mol•K), Cp(l)(liquid H2O) = 75.35 J/(mol•K), and Cp(g)(H2O gas) = 33.60 J/(mol•K).
-
How much heat is released in the conversion of 1.00 L of steam at 21.9 atm and 200°C to ice at −6.0°C and 1 atm?
-
How much heat must be applied to convert a 1.00 g piece of ice at −10°C to steam at 120°C?
-
How many grams of boiling water must be added to a glass with 25.0 g of ice at −3°C to obtain a liquid with a temperature of 45°C?
-
How many grams of ice at −5.0°C must be added to 150.0 g of water at 22°C to give a final temperature of 15°C?
Numerical Answers
-
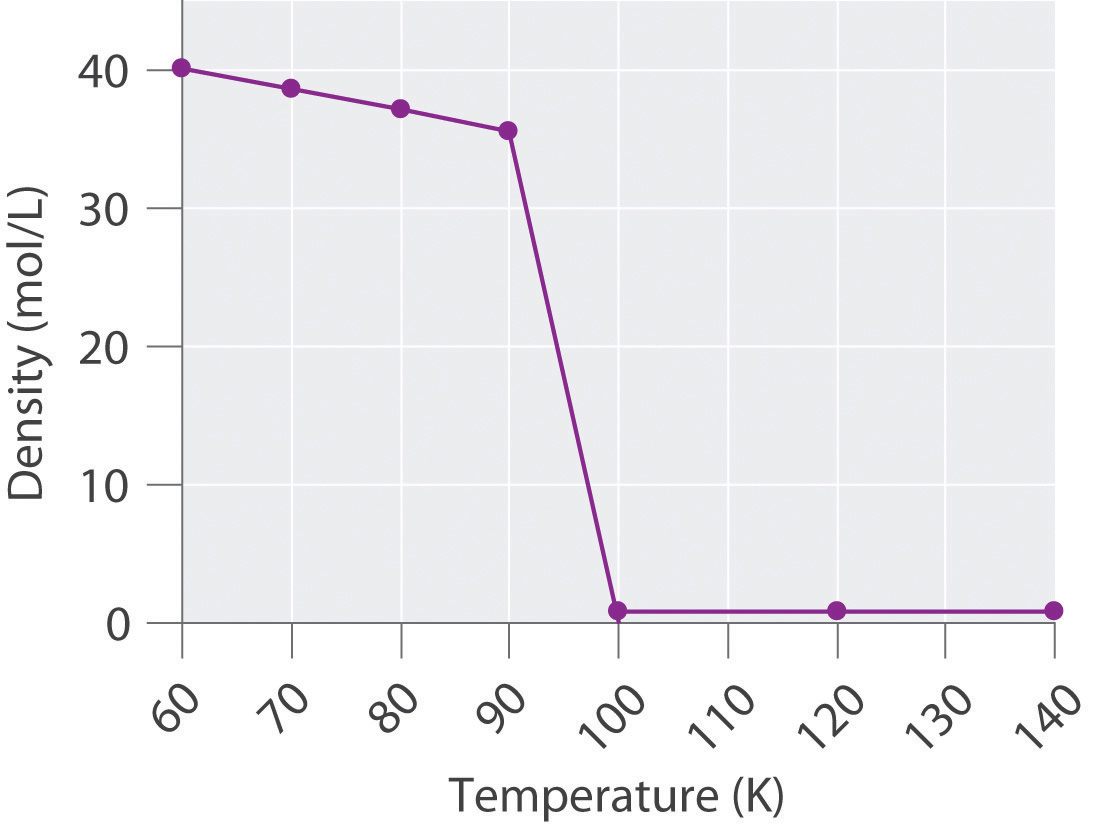
The transition from a liquid to a gaseous phase is accompanied by a drastic decrease in density. According to the data in the table and the plot, the boiling point of liquid oxygen is between 90 and 100 K (actually 90.2 K).
-
-
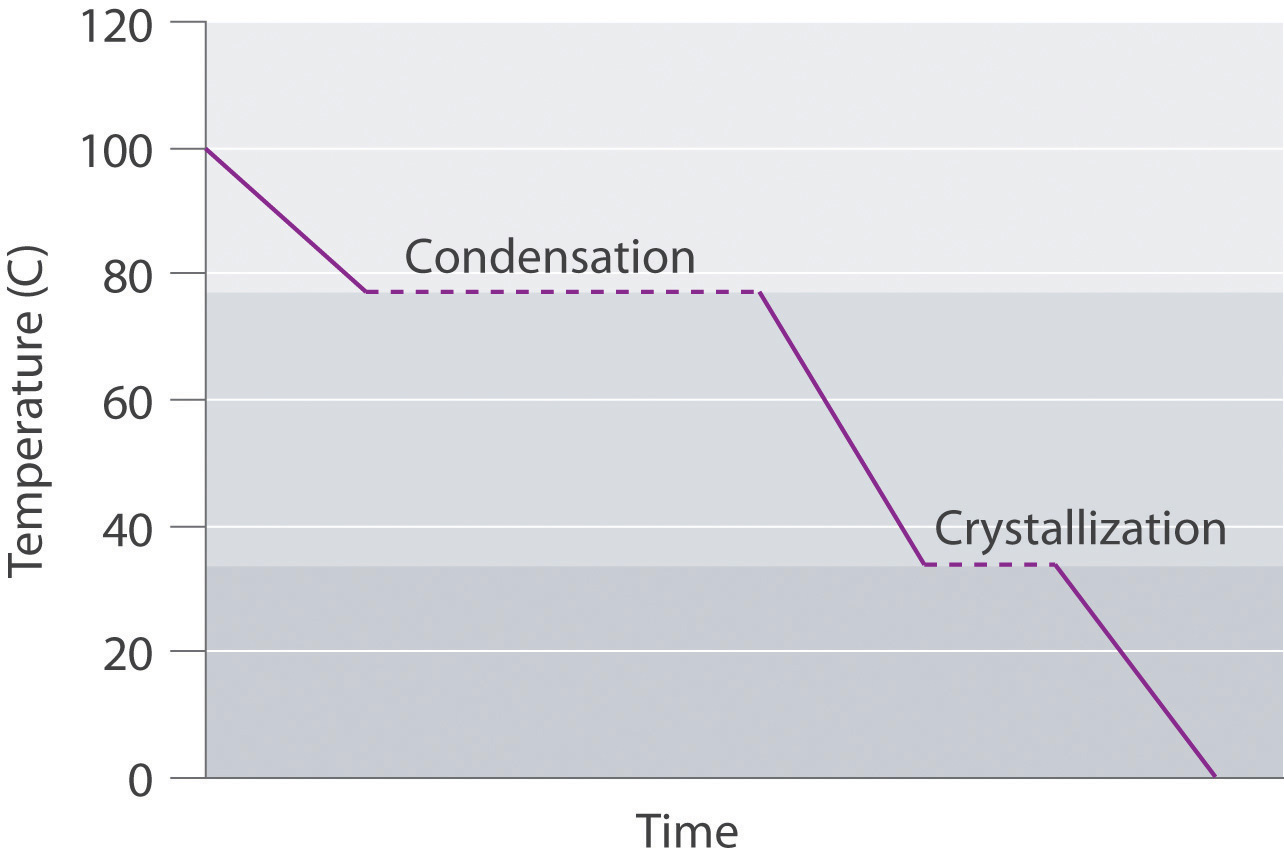
-
-
45.0 kJ/mol
-
-
488 kJ
-
-
32.6 kJ
-
-
57 g
11.5: Vapor Pressure
Conceptual Problems
-
What is the relationship between the boiling point, vapor pressure, and temperature of a substance and atmospheric pressure?
-
What is the difference between a volatile liquid and a nonvolatile liquid? Suppose that two liquid substances have the same molecular mass, but one is volatile and the other is nonvolatile. What differences in the molecular structures of the two substances could account for the differences in volatility?
-
An “old wives’ tale” states that applying ethanol to the wrists of a child with a very high fever will help to reduce the fever because blood vessels in the wrists are close to the skin. Is there a scientific basis for this recommendation? Would water be as effective as ethanol?
-
Why is the air over a strip of grass significantly cooler than the air over a sandy beach only a few feet away?
-
If gasoline is allowed to sit in an open container, it often feels much colder than the surrounding air. Explain this observation. Describe the flow of heat into or out of the system, as well as any transfer of mass that occurs. Would the temperature of a sealed can of gasoline be higher, lower, or the same as that of the open can? Explain your answer.
-
What is the relationship between the vapor pressure of a liquid and
- its temperature?
- the surface area of the liquid?
- the pressure of other gases on the liquid?
- its viscosity?
-
At 25°C, benzene has a vapor pressure of 12.5 kPa, whereas the vapor pressure of acetic acid is 2.1 kPa. Which is more volatile? Based on the intermolecular interactions in the two liquids, explain why acetic acid has the lower vapor pressure.
Numerical Problems
-
Acetylene (C2H2), which is used for industrial welding, is transported in pressurized cylinders. Its vapor pressure at various temperatures is given in the following table. Plot the data and use your graph to estimate the vapor pressure of acetylene at 293 K. Then use your graph to determine the value of ΔHvap for acetylene. How much energy is required to vaporize 2.00 g of acetylene at 250 K?
T (K) 145 155 175 200 225 250 300 P (mmHg) 1.3 7.8 32.2 190 579 1370 5093 -
The following table gives the vapor pressure of water at various temperatures. Plot the data and use your graph to estimate the vapor pressure of water at 25°C and at 75°C. What is the vapor pressure of water at 110°C? Use these data to determine the value of ΔHvap for water.
T (°C) 0 10 30 50 60 80 100 P (mmHg) 4.6 9.2 31.8 92.6 150 355 760 -
The ΔHvap of carbon tetrachloride is 29.8 kJ/mol, and its normal boiling point is 76.8°C. What is its boiling point at 0.100 atm?
-
The normal boiling point of sodium is 883°C. If ΔHvap is 97.4 kJ/mol, what is the vapor pressure (in millimeters of mercury) of liquid sodium at 300°C?
-
An unknown liquid has a vapor pressure of 0.860 atm at 63.7°C and a vapor pressure of 0.330 atm at 35.1°C. Use the data in Table 11.6 in Section 11.5 to identify the liquid.
-
An unknown liquid has a boiling point of 75.8°C at 0.910 atm and a boiling point of 57.2°C at 0.430 atm. Use the data in Table 11.6 in Section 11.5 to identify the liquid.
-
If the vapor pressure of a liquid is 0.850 atm at 20°C and 0.897 atm at 25°C, what is the normal boiling point of the liquid?
-
If the vapor pressure of a liquid is 0.799 atm at 99.0°C and 0.842 atm at 111°C, what is the normal boiling point of the liquid?
-
The vapor pressure of liquid SO2 is 33.4 torr at −63.4°C and 100.0 torr at −47.7 K.
- What is the ΔHvap of SO2?
- What is its vapor pressure at −24.5 K?
- At what temperature is the vapor pressure equal to 220 torr?
-
The vapor pressure of CO2 at various temperatures is given in the following table:
T (°C) −120 −110 −100 −90 P (torr) 9.81 34.63 104.81 279.5 - What is ΔHvap over this temperature range?
- What is the vapor pressure of CO2 at −70°C?
- At what temperature does CO2 have a vapor pressure of 310 torr?
Numerical Answers
-
vapor pressure at 273 K is 3050 mmHg; ΔHvap = 18.7 kJ/mol, 1.44 kJ
-
-
12.5°C
-
-
ΔHvap = 28.9 kJ/mol, n-hexane
-
-
ΔHvap = 7.81 kJ/mol, 36°C
11.6: Phase Diagrams
Conceptual Problems
- A phase diagram is a graphic representation of the stable phase of a substance at any combination of temperature and pressure. What do the lines separating different regions in a phase diagram indicate? What information does the slope of a line in a phase diagram convey about the physical properties of the phases it separates? Can a phase diagram have more than one point where three lines intersect?
- If the slope of the line corresponding to the solid/liquid boundary in the phase diagram of water were positive rather than negative, what would be the effect on aquatic life during periods of subzero temperatures? Explain your answer.
Conceptual Answer
-
The lines in a phase diagram represent boundaries between different phases; at any combination of temperature and pressure that lies on a line, two phases are in equilibrium. It is physically impossible for more than three phases to coexist at any combination of temperature and pressure, but in principle there can be more than one triple point in a phase diagram. The slope of the line separating two phases depends upon their relative densities. For example, if the solid–liquid line slopes up and to the right, the liquid is less dense than the solid, while if it slopes up and to the left, the liquid is denser than the solid.
Numerical Problems
- Naphthalene (C10H8) is the key ingredient in mothballs. It has normal melting and boiling points of 81°C and 218°C, respectively. The triple point of naphthalene is 80°C at 1000 Pa. Use these data to construct a phase diagram for naphthalene and label all the regions of your diagram.
- Argon is an inert gas used in welding. It has normal boiling and freezing points of 87.3 K and 83.8 K, respectively. The triple point of argon is 83.8 K at 0.68 atm. Use these data to construct a phase diagram for argon and label all the regions of your diagram.
11.7: Structure of Solids
Conceptual Problems
1. Compare the solid and liquid states in terms of
a. rigidity of structure.
b. long-range order.
c. short-range order.
2. How do amorphous solids differ from crystalline solids in each characteristic? Which of the two types of solid is most similar to a liquid?
a. rigidity of structure
b. long-range order
c. short-range order
3. Why is the arrangement of the constituent atoms or molecules more important in determining the properties of a solid than a liquid or a gas?
4. Why are the structures of solids usually described in terms of the positions of the constituent atoms rather than their motion?
5. What physical characteristics distinguish a crystalline solid from an amorphous solid? Describe at least two ways to determine experimentally whether a material is crystalline or amorphous.
6. Explain why each characteristic would or would not favor the formation of an amorphous solid.
a. slow cooling of pure molten material
b. impurities in the liquid from which the solid is formed
c. weak intermolecular attractive forces
7. A student obtained a solid product in a laboratory synthesis. To verify the identity of the solid, she measured its melting point and found that the material melted over a 12°C range. After it had cooled, she measured the melting point of the same sample again and found that this time the solid had a sharp melting point at the temperature that is characteristic of the desired product. Why were the two melting points different? What was responsible for the change in the melting point?
Conceptual Answers II
3. The arrangement of the atoms or molecules is more important in determining the properties of a solid because of the greater persistent long-range order of solids. Gases and liquids cannot readily be described by the spatial arrangement of their components because rapid molecular motion and rearrangement defines many of the properties of liquids and gases.
7. The initial solid contained the desired compound in an amorphous state, as indicated by the wide temperature range over which melting occurred. Slow cooling of the liquid caused it to crystallize, as evidenced by the sharp second melting point observed at the expected temperature.
Conceptual Problems II
- Why is it valid to represent the structure of a crystalline solid by the structure of its unit cell? What are the most important constraints in selecting a unit cell?
- All unit cell structures have six sides. Can crystals of a solid have more than six sides? Explain your answer.
- Explain how the intensive properties of a material are reflected in the unit cell. Are all the properties of a bulk material the same as those of its unit cell? Explain your answer.
- The experimentally measured density of a bulk material is slightly higher than expected based on the structure of the pure material. Propose two explanations for this observation.
- The experimentally determined density of a material is lower than expected based on the arrangement of the atoms in the unit cell, the formula mass, and the size of the atoms. What conclusion(s) can you draw about the material?
- Only one element (polonium) crystallizes with a simple cubic unit cell. Why is polonium the only example of an element with this structure?
- What is meant by the term coordination number in the structure of a solid? How does the coordination number depend on the structure of the metal?
- Arrange the three types of cubic unit cells in order of increasing packing efficiency. What is the difference in packing efficiency between the hcp structure and the ccp structure?
- The structures of many metals depend on pressure and temperature. Which structure—bcc or hcp—would be more likely in a given metal at very high pressures? Explain your reasoning.
- A metal has two crystalline phases. The transition temperature, the temperature at which one phase is converted to the other, is 95°C at 1 atm and 135°C at 1000 atm. Sketch a phase diagram for this substance. The metal is known to have either a ccp structure or a simple cubic structure. Label the regions in your diagram appropriately and justify your selection for the structure of each phase.
Numerical Problems II
- Metallic rhodium has an fcc unit cell. How many atoms of rhodium does each unit cell contain?
- Chromium has a structure with two atoms per unit cell. Is the structure of this metal simple cubic, bcc, fcc, or hcp?
- The density of nickel is 8.908 g/cm3. If the metallic radius of nickel is 125 pm, what is the structure of metallic nickel?
- The density of tungsten is 19.3 g/cm3. If the metallic radius of tungsten is 139 pm, what is the structure of metallic tungsten?
- An element has a density of 10.25 g/cm3 and a metallic radius of 136.3 pm. The metal crystallizes in a bcc lattice. Identify the element.
- A 21.64 g sample of a nonreactive metal is placed in a flask containing 12.00 mL of water; the final volume is 13.81 mL. If the length of the edge of the unit cell is 387 pm and the metallic radius is 137 pm, determine the packing arrangement and identify the element.
- A sample of an alkali metal that has a bcc unit cell is found to have a mass of 1.000 g and a volume of 1.0298 cm3. When the metal reacts with excess water, the reaction produces 539.29 mL of hydrogen gas at 0.980 atm and 23°C. Identify the metal, determine the unit cell dimensions, and give the approximate size of the atom in picometers.
- A sample of an alkaline earth metal that has a bcc unit cell is found to have a mass 5.000 g and a volume of 1.392 cm3. Complete reaction with chlorine gas requires 848.3 mL of chlorine gas at 1.050 atm and 25°C. Identify the metal, determine the unit cell dimensions, and give the approximate size of the atom in picometers.
- Lithium crystallizes in a bcc structure with an edge length of 3.509 Å. Calculate its density. What is the approximate metallic radius of lithium in picometers?
- Vanadium is used in the manufacture of rust-resistant vanadium steel. It forms bcc crystals with a density of 6.11 g/cm3 at 18.7°C. What is the length of the edge of the unit cell? What is the approximate metallic radius of the vanadium in picometers?
- A simple cubic cell contains one metal atom with a metallic radius of 100 pm.
- Determine the volume of the atom(s) contained in one unit cell [the volume of a sphere = (\({4 \over 3} \))πr3].
- What is the length of one edge of the unit cell? (Hint: there is no empty space between atoms.)
- Calculate the volume of the unit cell.
- Determine the packing efficiency for this structure.
- Use the steps in Problem 11 to calculate the packing efficiency for a bcc unit cell with a metallic radius of 1.00 Å.
Numerical Answers
1. four
3. fcc
5. molybdenum
7. sodium, unit cell edge = 428 pm, r = 185 pm
9. d = 0.5335 g/cm3, r =151.9 pm
11.8: Bonding in Solids
Conceptual Problems
1. Four vials labeled A–D contain sucrose, zinc, quartz, and sodium chloride, although not necessarily in that order. The following table summarizes the results of the series of analyses you have performed on the contents:
| A | B | C | D | |
|---|---|---|---|---|
| Melting Point | high | high | high | low |
| Thermal Conductivity | poor | poor | good | poor |
| Electrical Conductivity in Solid State | moderate | poor | high | poor |
| Electrical Conductivity in Liquid State | high | poor | high | poor |
| Hardness | hard | hard | soft | soft |
| Luster | none | none | high | none |
Match each vial with its contents.
2. Do ionic solids generally have higher or lower melting points than molecular solids? Why? Do ionic solids generally have higher or lower melting points than covalent solids? Explain your reasoning.
3. The strength of London dispersion forces in molecular solids tends to increase with molecular mass, causing a smooth increase in melting points. Some molecular solids, however, have significantly lower melting points than predicted by their molecular masses. Why?
4. Suppose you want to synthesize a solid that is both heat resistant and a good electrical conductor. What specific types of bonding and molecular interactions would you want in your starting materials?
5. Explain the differences between an interstitial alloy and a substitutional alloy. Given an alloy in which the identity of one metallic element is known, how could you determine whether it is a substitutional alloy or an interstitial alloy?
6. How are intermetallic compounds different from interstitial alloys or substitutional alloys?
Conceptual Answers
1.
a. NaCl, ionic solid
b. quartz, covalent solid
c. zinc, metal
d. sucrose, molecular solid
5. In a substitutional alloy, the impurity atoms are similar in size and chemical properties to the atoms of the host lattice; consequently, they simply replace some of the metal atoms in the normal lattice and do not greatly perturb the structure and physical properties. In an interstitial alloy, the impurity atoms are generally much smaller, have very different chemical properties, and occupy holes between the larger metal atoms. Because interstitial impurities form covalent bonds to the metal atoms in the host lattice, they tend to have a large effect on the mechanical properties of the metal, making it harder, less ductile, and more brittle. Comparing the mechanical properties of an alloy with those of the parent metal could be used to decide whether the alloy were a substitutional or interstitial alloy.
Numerical Problems
1. Will the melting point of lanthanum(III) oxide be higher or lower than that of ferrous bromide? The relevant ionic radii are as follows: La3+, 104 pm; O2−, 132 pm; Fe2+, 83 pm; and Br−, 196 pm. Explain your reasoning.
2. Draw a graph showing the relationship between the electrical conductivity of metallic silver and temperature.
3. Which has the higher melting point? Explain your reasoning in each case.
a. Os or Hf
b. SnO2 or ZrO2
c. Al2O3 or SiO2
4. Draw a graph showing the relationship between the electrical conductivity of a typical semiconductor and temperature.
Numerical Answer
3.
a. Osmium has a higher melting point, due to more valence electrons for metallic bonding.
b. Zirconium oxide has a higher melting point, because it has greater ionic character.
c. Aluminum oxide has a higher melting point, again because it has greater ionic character.

