10.E: Gases (Exercises)

Last updated
Save as PDF

Page ID: 24747

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Template:PrintMe

10.1: Characteristics of Gases

Conceptual Problems

Q10.1.1

Explain the differences between the microscopic and the macroscopic properties of matter. Is the boiling point of a compound a microscopic or macroscopic property? molecular mass? Why?

Q10.1.2

How do the microscopic properties of matter influence the macroscopic properties? Can you relate molecular mass to boiling point? Why or why not?

Q10.1.3

For a substance that has gas, liquid, and solid phases, arrange these phases in order of increasing density.

strength of intermolecular interactions.
compressibility.
molecular motion.
order in the arrangement of the molecules or atoms.

Q10.1.4

Which elements of the periodic table exist as gases at room temperature and pressure? Of these, which are diatomic molecules and which are monatomic? Which elements are liquids at room temperature and pressure? Which portion of the periodic table contains elements whose binary hydrides are most likely gases at room temperature?

10.2: Pressure

Q10.2.1

What four quantities must be known to completely describe a sample of a gas? What units are commonly used for each quantity?

Q10.2.2

If the applied force is constant, how does the pressure exerted by an object change as the area on which the force is exerted decreases? In the real world, how does this relationship apply to the ease of driving a small nail versus a large nail?

Q10.2.3

As the force on a fixed area increases, does the pressure increase or decrease? With this in mind, would you expect a heavy person to need smaller or larger snowshoes than a lighter person? Explain.

Q10.2.4

What do we mean by barometric pressure? Is the barometric pressure at the summit of Mt. Rainier greater than or less than the pressure in Miami, Florida? Why?

Q10.2.5

Which has the highest barometric pressure—a cave in the Himalayas, a mine in South Africa, or a beach house in Florida? Which has the lowest?

Q10.2.6

Mars has an average barometric pressure of 0.007 atm. Would it be easier or harder to drink liquid from a straw on Mars than on Earth? Explain your answer.

Q10.2.7

Is the pressure exerted by a 1.0 kg mass on a 2.0 m² area greater than or less than the pressure exerted by a 1.0 kg mass on a 1.0 m² area? What is the difference, if any, between the pressure of the atmosphere exerted on a 1.0 m² piston and a 2.0 m² piston?

Q10.2.8

If you used water in a barometer instead of mercury, what would be the major difference in the instrument?

Numerical Problems

Q10.2.9

Calculate the pressure in pascals and in atmospheres exerted by a carton of milk that weighs 1.5 kg and has a base of 7.0 cm × 7.0 cm. If the carton were lying on its side (height = 25 cm), would it exert more or less pressure? Explain your reasoning.

Q10.2.10

If barometric pressure at sea level is 1.0 × 10⁵ Pa, what is the mass of air in kilograms above a 1.0 cm² area of your skin as you lie on the beach? If barometric pressure is 8.2 × 10⁴ Pa on a mountaintop, what is the mass of air in kilograms above a 4.0 cm² patch of skin?

Q10.2.11

Complete the following table:

atm	kPa	mmHg
1.40
		723
	43.2

Q10.2.12

The SI unit of pressure is the pascal, which is equal to 1 N/m². Show how the product of the mass of an object and the acceleration due to gravity result in a force that, when exerted on a given area, leads to a pressure in the correct SI units. What mass in kilograms applied to a 1.0 cm² area is required to produce a pressure of

1.0 atm?
1.0 torr?
1 mmHg?
1 kPa?

Q10.2.13

If you constructed a manometer to measure gas pressures over the range 0.60–1.40 atm using the liquids given in the following table, how tall a column would you need for each liquid? The density of mercury is 13.5 g/cm³. Based on your results, explain why mercury is still used in barometers, despite its toxicity.

	Liquid Density (20°C)	Column Height (m)
isopropanol	0.785
coconut oil	0.924
glycerine	1.259

10.3: The Gas Laws

Conceptual Problems

Q10.3.1

Sketch a graph of the volume of a gas versus the pressure on the gas. What would the graph of V versus P look like if volume was directly proportional to pressure?

S10.3.1

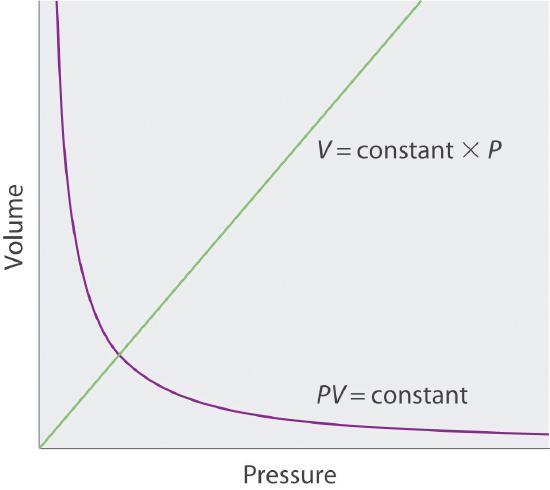
Q10.3.2

What properties of a gas are described by Boyle’s law, Charles’s law, and Avogadro’s law? In each law, what quantities are held constant? Why does the constant in Boyle’s law depend on the amount of gas used and the temperature at which the experiments are carried out?

Q10.3.3

Use Charles’s law to explain why cooler air sinks.

Q10.3.4

Use Boyle’s law to explain why it is dangerous to heat even a small quantity of water in a sealed container.

Numerical Problems

Q10.3.5

A 1.00 mol sample of gas at 25°C and 1.0 atm has an initial volume of 22.4 L. Calculate the results of each change, assuming all the other conditions remain constant.

The pressure is changed to 85.7 mmHg. How many milliliters does the gas occupy?
The volume is reduced to 275 mL. What is the pressure in millimeters of mercury?
The pressure is increased to 25.3 atm. What is the temperature in degrees Celsius?
The sample is heated to 30°C. What is the volume in liters?
The sample is compressed to 1255 mL, and the pressure is increased to 2555 torr. What is the temperature of the gas in kelvins?

S10.3.5

1.99 × 10⁵ mL
6.19 × 10⁴ mmHg
7270°C
22.8 L
51.4 K

Q10.3.6

A 1.00 mol sample of gas is at 300 K and 4.11 atm. What is the volume of the gas under these conditions? The sample is compressed to 6.0 atm at constant temperature, giving a volume of 3.99 L. Is this result consistent with Boyle’s law?

10.4: The Ideal Gas Equation

Conceptual Problems

Q10.4.1

For an ideal gas, is volume directly proportional or inversely proportional to temperature? What is the volume of an ideal gas at absolute zero?

Q10.4.2

What is meant by STP? If a gas is at STP, what further information is required to completely describe the state of the gas?

Q10.4.3

For a given amount of a gas, the volume, temperature, and pressure under any one set of conditions are related to the volume, the temperature, and the pressure under any other set of conditions by the equation

\[ \dfrac{P_1V_1}{T_1} = \dfrac{P_2V_2}{T_2} \]

Q10.4.4

Derive this equation from the ideal gas law. At constant temperature, this equation reduces to one of the gas laws discussed previosuly; which one? At constant pressure, this equation reduces to one of the laws discussed in Section 10.3"; which one?

Q10.4.5

Predict the effect of each change on one variable if the other variables are held constant.

If the number of moles of gas increases, what is the effect on the temperature of the gas?
If the temperature of a gas decreases, what is the effect on the pressure of the gas?
If the volume of a gas increases, what is the effect on the temperature of the gas?
If the pressure of a gas increases, what is the effect on the number of moles of the gas?

Q10.4.6

What would the ideal gas law be if the following were true?

volume were proportional to pressure
temperature were proportional to amount
pressure were inversely proportional to temperature
volume were inversely proportional to temperature
both pressure and volume were inversely proportional to temperature

Given the following initial and final values, what additional information is needed to solve the problem using the ideal gas law?

Given	Solve for
V₁, T₁, T₂, n₁	n ₂
P₁, P₂, T₂, n₂	n ₁
T₁, T₂	V ₂
P₁, n₁	P ₂

Q10.4.7

Given the following information and using the ideal gas law, what equation would you use to solve the problem?

Given	Solve for
P₁, P₂, T₁	T ₂
V₁, n₁, n₂	V ₂
T₁, T₂, V₁, V₂, n₂	n ₁

Q10.4.8

Using the ideal gas law as a starting point, derive the relationship between the density of a gas and its molar mass. Which would you expect to be denser—nitrogen or oxygen? Why does radon gas accumulate in basements and mine shafts?

Q10.4.9

Use the ideal gas law to derive an equation that relates the remaining variables for a sample of an ideal gas if the following are held constant.

amount and volume
pressure and amount
temperature and volume
temperature and amount
pressure and temperature

S10.4.9

P/T = constant
V/T = constant (Charles’ law)
P/n = constant
PV = constant (Boyle’s law)
V/n = constant (Avogadro’s law)

Q10.4.10

Tennis balls that are made for Denver, Colorado, feel soft and do not bounce well at lower altitudes. Use the ideal gas law to explain this observation. Will a tennis ball designed to be used at sea level be harder or softer and bounce better or worse at higher altitudes?

Numerical Problems

Q10.4.11

Calculate the number of moles in each sample at STP.

1580 mL of NO₂
847 cm³ of HCl
4.792 L of H₂
a 15.0 cm × 6.7 cm × 7.5 cm container of ethane

S10.4.11

7.05 × 10⁻² mol
3.78 × 10⁻² mol
0.2138 mol
3.4 × 10⁻² mol

Q10.4.12

Calculate the number of moles in each sample at STP.

2200 cm³ of CO₂
1200 cm³ of N₂
3800 mL of SO₂
13.75 L of NH₃

Q10.4.13

Calculate the mass of each sample at STP.

36 mL of HI
550 L of H₂S
1380 cm³ of CH₄

S10.4.13

0.21 g HI;
840 g H₂S;
0.988 g CH₄

Q10.4.14

Calculate the mass of each sample at STP.

3.2 L of N₂O
65 cm³ of Cl₂
3600 mL of HBr

Q10.4.15

Calculate the volume in liters of each sample at STP.

1.68 g of Kr
2.97 kg of propane (C₃H₈)
0.643 mg of (CH₃)₂O

S10.4.15

0.449 L Kr
1510 L C₃H₈
3.13 × 10⁻⁴ L (CH₃)₂O

Q10.4.16

Calculate the volume in liters of each sample at STP.

3.2 g of Xe
465 mg of CS₂
5.34 kg of acetylene (C₂H₂)

Q10.4.17

Calculate the volume of each gas at STP.

1.7 L at 28°C and 96.4 kPa
38.0 mL at 17°C and 103.4 torr
650 mL at −15°C and 723 mmHg

Q10.4.18

Calculate the volume of each gas at STP.

2.30 L at 23°C and 740 mmHg
320 mL at 13°C and 97.2 kPa
100.5 mL at 35°C and 1.4 atm

S10.4.18

1.5 L
4.87 mL
650 mL

Q10.4.19

A 8.60 L tank of nitrogen gas at a pressure of 455 mmHg is connected to an empty tank with a volume of 5.35 L. What is the final pressure in the system after the valve connecting the two tanks is opened? Assume that the temperature is constant.

S10.4.19

281 mmHg

Q10.4.20

At constant temperature, what pressure in atmospheres is needed to compress 14.2 L of gas initially at 25.2 atm to a volume of 12.4 L? What pressure is needed to compress 27.8 L of gas to 20.6 L under similar conditions?

Q10.4.21

One method for preparing hydrogen gas is to pass HCl gas over hot aluminum; the other product of the reaction is AlCl₃. If you wanted to use this reaction to fill a balloon with a volume of 28,500 L at sea level and a temperature of 78°F, what mass of aluminum would you need? What volume of HCl at STP would you need?

S10.4.21

20.9 kg Al, 5.20 × 10⁴ L HCl

Q10.4.21

An 3.50 g sample of acetylene is burned in excess oxygen according to the following reaction:

\[\ce{2 C2H2(g) + 5 O2(g) → 4 CO2(g) + 2 H2O(l)}\]

At STP, what volume of CO₂(g) is produced?

Q10.4.22

Calculate the density of ethylene (C₂H₄) under each set of conditions.

7.8 g at 0.89 atm and 26°C
6.3 mol at 102.6 kPa and 38°C
9.8 g at 3.1 atm and −45°C

S10.4.22

1.0 g/L
1.1 g/L
4.6 g/L

Q10.4.23

Determine the density of O₂ under each set of conditions.

42 g at 1.1 atm and 25°C
0.87 mol at 820 mmHg and 45°C
16.7 g at 2.4 atm and 67°C

Q10.4.24

At 140°C, the pressure of a diatomic gas in a 3.0 L flask is 635 kPa. The mass of the gas is 88.7 g. What is the most likely identity of the gas?

Q10.4.25

What volume must a balloon have to hold 6.20 kg of H₂ for an ascent from sea level to an elevation of 20,320 ft, where the temperature is −37°C and the pressure is 369 mmHg?

Q10.4.26

What must be the volume of a balloon that can hold 313.0 g of helium gas and ascend from sea level to an elevation of 1.5 km, where the temperature is 10.0°C and the pressure is 635.4 mmHg?

S10.4.26

2174 L

Q10.4.27

A typical automobile tire is inflated to a pressure of 28.0 lb/in.² Assume that the tire is inflated when the air temperature is 20°C; the car is then driven at high speeds, which increases the temperature of the tire to 43°C. What is the pressure in the tire? If the volume of the tire had increased by 8% at the higher temperature, what would the pressure be?

Q10.4.28

The average respiratory rate for adult humans is 20 breaths per minute. If each breath has a volume of 310 mL of air at 20°C and 0.997 atm, how many moles of air does a person inhale each day? If the density of air is 1.19 kg/m³, what is the average molecular mass of air?

Q10.4.29

Kerosene has a self-ignition temperature of 255°C. It is a common accelerant used by arsonists, but its presence is easily detected in fire debris by a variety of methods. If a 1.0 L glass bottle containing a mixture of air and kerosene vapor at an initial pressure of 1 atm and an initial temperature of 23°C is pressurized, at what pressure would the kerosene vapor ignite?

10.5: Further Applications of the Ideal-Gas Equations

Conceptual Problems

Q10.5.1

Why are so many industrially important reactions carried out in the gas phase?

Q10.5.2

The volume of gas produced during a chemical reaction can be measured by collecting the gas in an inverted container filled with water. The gas forces water out of the container, and the volume of liquid displaced is a measure of the volume of gas. What additional information must be considered to determine the number of moles of gas produced? The volume of some gases cannot be measured using this method. What property of a gas precludes the use of this method?

Q10.5.3

Equal masses of two solid compounds (A and B) are placed in separate sealed flasks filled with air at 1 atm and heated to 50°C for 10 hours. After cooling to room temperature, the pressure in the flask containing A was 1.5 atm. In contrast, the pressure in the flask containing B was 0.87 atm. Suggest an explanation for these observations. Would the masses of samples A and B still be equal after the experiment? Why or why not?

Numerical Problems

Q10.5.4

Balance each chemical equation and then determine the volume of the indicated reactant at STP that is required for complete reaction. Assuming complete reaction, what is the volume of the products?

SO₂(g) + O₂(g) → SO₃(g) given 2.4 mol of O₂
H₂(g) + Cl₂(g) → HCl(g) given 0.78 g of H₂
C₂H₆(g) + O₂(g) → CO₂(g) + H₂O(g) given 1.91 mol of O₂

Q10.5.5

During the smelting of iron, carbon reacts with oxygen to produce carbon monoxide, which then reacts with iron(III) oxide to produce iron metal and carbon dioxide. If 1.82 L of CO₂ at STP is produced,

what mass of CO is consumed?
what volume of CO at STP is consumed?
how much O₂ (in liters) at STP is used?
what mass of carbon is consumed?
how much iron metal (in grams) is produced?

Q10.5.6

Complete decomposition of a sample of potassium chlorate produced 1.34 g of potassium chloride and oxygen gas.

What is the mass of KClO₃ in the original sample?
What mass of oxygen is produced?
What is the volume of oxygen produced at STP?

S10.5.6

2.20 g KClO₃
0.863 g O₂
604 mL O₂

Q10.5.7

The combustion of a 100.0 mg sample of an herbicide in excess oxygen produced 83.16 mL of CO₂ and 72.9 mL of H₂O vapor at STP. A separate analysis showed that the sample contained 16.44 mg of chlorine. If the sample is known to contain only C, H, Cl, and N, determine the percent composition and the empirical formula of the herbicide.

Q10.5.8

The combustion of a 300.0 mg sample of an antidepressant in excess oxygen produced 326 mL of CO₂ and 164 mL of H₂O vapor at STP. A separate analysis showed that the sample contained 23.28% oxygen. If the sample is known to contain only C, H, O, and N, determine the percent composition and the empirical formula of the antidepressant.

S10.5.8

Percent composition: 58.3% C, 4.93% H, 23.28% O, and 13.5% N; empirical formula: C₁₀H₁₀O₃N₂

10.6: Gas Mixtures and Partial Pressures

Conceptual Problems

Q10.6.1

Dalton’s law of partial pressures makes one key assumption about the nature of the intermolecular interactions in a mixture of gases. What is it?

Q10.6.2

What is the relationship between the partial pressure of a gas and its mole fraction in a mixture?

Numerical Problems

Q10.6.3

What is the partial pressure of each gas if the following amounts of substances are placed in a 25.0 L container at 25°C? What is the total pressure of each mixture?

1.570 mol of CH₄ and 0.870 mol of CO₂
2.63 g of CO and 1.24 g of NO₂
1.78 kg of CH₃Cl and 0.92 kg of SO₂

Q10.6.4

What is the partial pressure of each gas in the following 3.0 L mixtures at 37°C as well as the total pressure?

0.128 mol of SO₂ and 0.098 mol of methane (CH₄)
3.40 g of acetylene (C₂H₂) and 1.54 g of He
0.267 g of NO, 4.3 g of Ar, and 0.872 g of SO₂

Q10.6.5

In a mixture of helium, oxygen, and methane in a 2.00 L container, the partial pressures of He and O₂ are 13.6 kPa and 29.2 kPa, respectively, and the total pressure inside the container is 95.4 kPa. What is the partial pressure of methane? If the methane is ignited to initiate its combustion with oxygen and the system is then cooled to the original temperature of 30°C, what is the final pressure inside the container (in kilopascals)?

S10.6.5

52.6 kPa, 66.2 kPa

Q10.6.6

A 2.00 L flask originally contains 1.00 g of ethane (C₂H₆) and 32.0 g of oxygen at 21°C. During ignition, the ethane reacts completely with oxygen to produce CO₂ and water vapor, and the temperature of the flask increases to 200°C. Determine the total pressure and the partial pressure of each gas before and after the reaction.

Q10.6.7

If a 20.0 L cylinder at 19°C is charged with 5.0 g each of sulfur dioxide and oxygen, what is the partial pressure of each gas? The sulfur dioxide is ignited in the oxygen to produce sulfur trioxide gas, and the mixture is allowed to cool to 19°C at constant pressure. What is the final volume of the cylinder? What is the partial pressure of each gas in the piston?

Q10.6.8

The highest point on the continent of Europe is Mt. Elbrus in Russia, with an elevation of 18,476 ft. The highest point on the continent of South America is Mt. Aconcagua in Argentina, with an elevation of 22,841 ft.

The following table shows the variation of atmospheric pressure with elevation. Use the data in the table to construct a plot of pressure versus elevation.

Elevation (km)	Pressure in Summer (mmHg)	Pressure in Winter (mmHg)
0.0	760.0	760.0
1.0	674.8	670.6
1.5	635.4	629.6
2.0	598.0	590.8
3.0	528.9	519.7
5.0	410.6	398.7
7.0	314.9	301.6
9.0	237.8	224.1

Use your graph to estimate the pressures in millimeters of mercury during the summer and the winter at the top of both mountains in both atmospheres and kilopascals.
Given that air is 20.95% O₂ by volume, what is the partial pressure of oxygen in atmospheres during the summer at each location?

10.7: Kinetic-Molecular Theory

10.8: Molecular Effusion and Diffusion

Conceptual Problems

Q10.8.1

Which of the following processes represents effusion, and which represents diffusion?

helium escaping from a hole in a balloon
vapor escaping from the surface of a liquid
gas escaping through a membrane

Q10.8.2

Which postulate of the kinetic molecular theory of gases most readily explains the observation that a helium-filled balloon is round?

Q10.8.3

Why is it relatively easy to compress a gas? How does the compressibility of a gas compare with that of a liquid? A solid? Why? Which of the postulates of the kinetic molecular theory of gases most readily explains these observations?

Q10.8.4

What happens to the average kinetic energy of a gas if the rms speed of its particles increases by a factor of 2? How is the rms speed different from the average speed?

Q10.8.5

Which gas—radon or helium—has a higher average kinetic energy at 100°C? Which has a higher average speed? Why? Which postulate of the kinetic molecular theory of gases most readily supports your answer?

Q10.8.6

What is the relationship between the average speed of a gas particle and the temperature of the gas? What happens to the distribution of molecular speeds if the temperature of a gas is increased? Decreased?

Q10.8.7

Qualitatively explain the relationship between the number of collisions of gas particles with the walls of a container and the pressure of a gas. How does increasing the temperature affect the number of collisions?

Q10.8.8

What happens to the average kinetic energy of a gas at constant temperature if the

volume of the gas is increased?
pressure of the gas is increased?

Q10.8.9

What happens to the density of a gas at constant temperature if the

volume of the gas is increased?
pressure of the gas is increased?

Q10.8.10

Use the kinetic molecular theory of gases to describe how a decrease in volume produces an increase in pressure at constant temperature. Similarly, explain how a decrease in temperature leads to a decrease in volume at constant pressure.

Q10.8.11

Graham’s law is valid only if the two gases are at the same temperature. Why?

Q10.8.12

If we lived in a helium atmosphere rather than in air, would we detect odors more or less rapidly than we do now? Explain your reasoning. Would we detect odors more or less rapidly at sea level or at high altitude? Why?

Numerical Problems

Q10.8.13

At a given temperature, what is the ratio of the rms speed of the atoms of Ar gas to the rms speed of molecules of H₂ gas?

S10.8.13

At any temperature, the rms speed of hydrogen is 4.45 times that of argon.

Q10.8.14

At a given temperature, what is the ratio of the rms speed of molecules of CO gas to the rms speed of molecules of H₂S gas?

Q10.8.15

What is the ratio of the rms speeds of argon and oxygen at any temperature? Which diffuses more rapidly?

Q10.8.16

What is the ratio of the rms speeds of Kr and NO at any temperature? Which diffuses more rapidly?

Q10.8.17

Deuterium (D) and tritium (T) are heavy isotopes of hydrogen. Tritium has an atomic mass of 3.016 amu and has a natural abundance of 0.000138%. The effusion of hydrogen gas (containing a mixture of H₂, HD, and HT molecules) through a porous membrane can be used to obtain samples of hydrogen that are enriched in tritium. How many membrane passes are necessary to give a sample of hydrogen gas in which 1% of the hydrogen molecules are HT?

Q10.8.18

Samples of HBr gas and NH₃ gas are placed at opposite ends of a 1 m tube. If the two gases are allowed to diffuse through the tube toward one another, at what distance from each end of the tube will the gases meet and form solid NH₄Br?

10.9: Real Gases: Deviations from Ideal Behavior

Conceptual Problems

Q10.9.1

What factors cause deviations from ideal gas behavior? Use a sketch to explain your answer based on interactions at the molecular level.

Q10.9.2

Explain the effect of nonzero atomic volume on the ideal gas law at high pressure. Draw a typical graph of volume versus 1/P for an ideal gas and a real gas.

Q10.9.3

For an ideal gas, the product of pressure and volume should be constant, regardless of the pressure. Experimental data for methane, however, show that the value of PV decreases significantly over the pressure range 0 to 120 atm at 0°C. The decrease in PV over the same pressure range is much smaller at 100°C. Explain why PV decreases with increasing temperature. Why is the decrease less significant at higher temperatures.

Q10.9.4

What is the effect of intermolecular forces on the liquefaction of a gas? At constant pressure and volume, does it become easier or harder to liquefy a gas as its temperature increases? Explain your reasoning. What is the effect of increasing the pressure on the liquefaction temperature?

Q10.9.5

Describe qualitatively what a and b, the two empirical constants in the van der Waals equation, represent.

Q10.9.6

In the van der Waals equation, why is the term that corrects for volume negative and the term that corrects for pressure positive? Why is n/V squared?

Q10.9.7

Liquefaction of a gas depends strongly on two factors. What are they? As temperature is decreased, which gas will liquefy first—ammonia, methane, or carbon monoxide? Why?

Q10.9.8

What is a cryogenic liquid? Describe three uses of cryogenic liquids.

Q10.9.9

Air consists primarily of O₂, N₂, Ar, Ne, Kr, and Xe. Use the concepts discussed in this chapter to propose two methods by which air can be separated into its components. Which component of air will be isolated first?

Q10.9.10

How can gas liquefaction facilitate the storage and transport of fossil fuels? What are the potential drawbacks to these methods?

Numerical Problems

Q10.9.11

The van der Waals constants for xenon are a = 4.19 (L²·atm)/mol² and b = 0.0510 L/mol. If a 0.250 mol sample of xenon in a container with a volume of 3.65 L is cooled to −90°C, what is the pressure of the sample assuming ideal gas behavior? What would be the actual pressure under these conditions?

Q10.9.12

The van der Waals constants for water vapor are a = 5.46 (L²·atm)/mol² and b = 0.0305 L/mol. If a 20.0 g sample of water in a container with a volume of 5.0 L is heated to 120°C, what is the pressure of the sample assuming ideal gas behavior? What would be the actual pressure under these conditions?