21.6: Biological Effects of Radiation
- Page ID
- 414758
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Describe the biological impact of ionizing radiation
- Define units for measuring radiation exposure
- Explain the operation of common tools for detecting radioactivity
- List common sources of radiation exposure in the US
The increased use of radioisotopes has led to increased concerns over the effects of these materials on biological systems (such as humans). All radioactive nuclides emit high-energy particles or electromagnetic waves. When this radiation encounters living cells, it can cause heating, break chemical bonds, or ionize molecules. The most serious biological damage results when these radioactive emissions fragment or ionize molecules. For example, alpha and beta particles emitted from nuclear decay reactions possess much higher energies than ordinary chemical bond energies. When these particles strike and penetrate matter, they produce ions and molecular fragments that are extremely reactive. The damage this does to biomolecules in living organisms can cause serious malfunctions in normal cell processes, taxing the organism’s repair mechanisms and possibly causing illness or even death (Figure \(\PageIndex{1}\)).
Ionizing and Nonionizing Radiation
There is a large difference in the magnitude of the biological effects of nonionizing radiation (for example, light and microwaves) and ionizing radiation, emissions energetic enough to knock electrons out of molecules (for example, α and β particles, γ rays, X-rays, and high-energy ultraviolet radiation) (Figure \(\PageIndex{2}\)).
Energy absorbed from nonionizing radiation speeds up the movement of atoms and molecules, which is equivalent to heating the sample. Although biological systems are sensitive to heat (as we might know from touching a hot stove or spending a day at the beach in the sun), a large amount of nonionizing radiation is necessary before dangerous levels are reached. Ionizing radiation, however, may cause much more severe damage by breaking bonds or removing electrons in biological molecules, disrupting their structure and function. The damage can also be done indirectly, by first ionizing H2O (the most abundant molecule in living organisms), which forms a H2O+ ion that reacts with water, forming a hydronium ion and a hydroxyl radical:
Because the hydroxyl radical has an unpaired electron, it is highly reactive. (This is true of any substance with unpaired electrons, known as a free radical.) This hydroxyl radical can react with all kinds of biological molecules (DNA, proteins, enzymes, and so on), causing damage to the molecules and disrupting physiological processes. Examples of direct and indirect damage are shown in Figure 21.32.
Biological Effects of Exposure to Radiation
Radiation can harm either the whole body (somatic damage) or eggs and sperm (genetic damage). Its effects are more pronounced in cells that reproduce rapidly, such as the stomach lining, hair follicles, bone marrow, and embryos. This is why patients undergoing radiation therapy often feel nauseous or sick to their stomach, lose hair, have bone aches, and so on, and why particular care must be taken when undergoing radiation therapy during pregnancy.
Different types of radiation have differing abilities to pass through material (Figure \(\PageIndex{3}\)). A very thin barrier, such as a sheet or two of paper, or the top layer of skin cells, usually stops alpha particles. Because of this, alpha particle sources are usually not dangerous if outside the body, but are quite hazardous if ingested or inhaled (see the Chemistry in Everyday Life feature on Radon Exposure). Beta particles will pass through a hand, or a thin layer of material like paper or wood, but are stopped by a thin layer of metal. Gamma radiation is very penetrating and can pass through a thick layer of most materials. Some high-energy gamma radiation is able to pass through a few feet of concrete. Certain dense, high atomic number elements (such as lead) can effectively attenuate gamma radiation with thinner material and are used for shielding. The ability of various kinds of emissions to cause ionization varies greatly, and some particles have almost no tendency to produce ionization. Alpha particles have about twice the ionizing power of fast-moving neutrons, about 10 times that of β particles, and about 20 times that of γ rays and X-rays.
For many people, one of the largest sources of exposure to radiation is from radon gas (Rn-222). Radon-222 is an α emitter with a half–life of 3.82 days. It is one of the products of the radioactive decay series of U-238 (Figure 21.9), which is found in trace amounts in soil and rocks. The radon gas that is produced slowly escapes from the ground and gradually seeps into homes and other structures above. Since it is about eight times more dense than air, radon gas accumulates in basements and lower floors, and slowly diffuses throughout buildings (Figure \(\PageIndex{4}\)).

Radon is found in buildings across the country, with amounts depending on where you live. The average concentration of radon inside houses in the US (1.25 pCi/L) is about three times the levels found in outside air, and about one in six houses have radon levels high enough that remediation efforts to reduce the radon concentration are recommended. Exposure to radon increases one’s risk of getting cancer (especially lung cancer), and high radon levels can be as bad for health as smoking a carton of cigarettes a day. Radon is the number one cause of lung cancer in nonsmokers and the second leading cause of lung cancer overall. Radon exposure is believed to cause over 20,000 deaths in the US per year.
Measuring Radiation Exposure
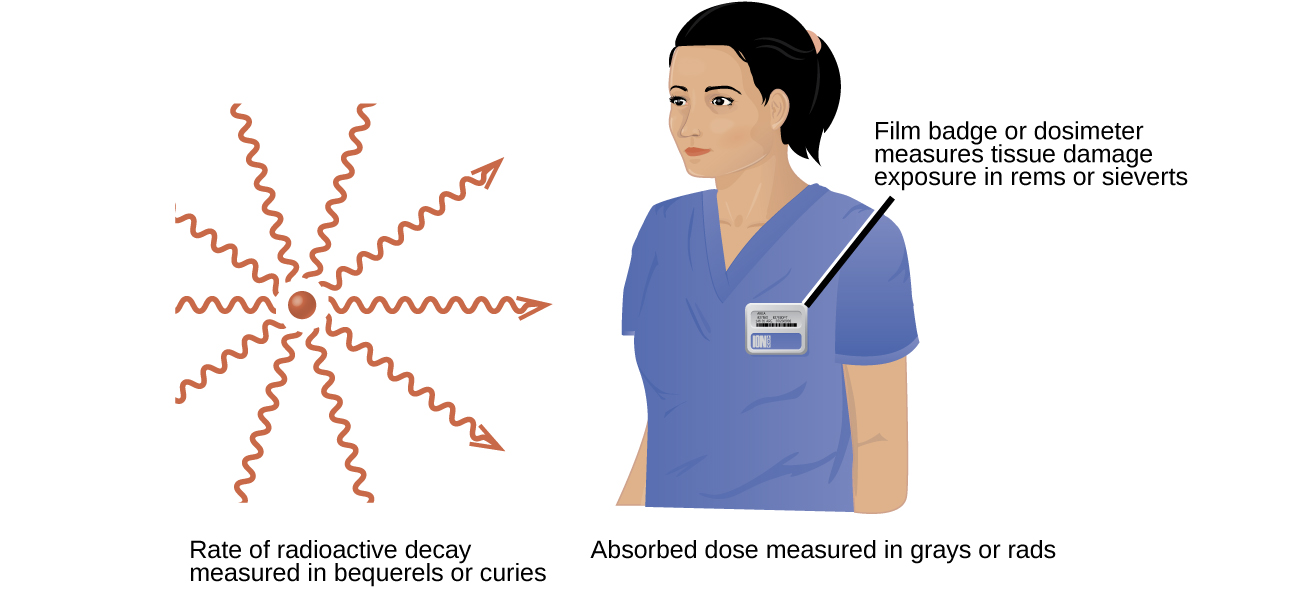
Several different devices are used to detect and measure radiation, including Geiger counters, scintillation counters (scintillators), and radiation dosimeters (Figure \(\PageIndex{5}\)). Probably the best-known radiation instrument, the Geiger counter (also called the Geiger-Müller counter) detects and measures radiation. Radiation causes the ionization of the gas in a Geiger-Müller tube. The rate of ionization is proportional to the amount of radiation. A scintillation counter contains a scintillator—a material that emits light (luminesces) when excited by ionizing radiation—and a sensor that converts the light into an electric signal. Radiation dosimeters also measure ionizing radiation and are often used to determine personal radiation exposure. Commonly used types are electronic, film badge, thermoluminescent, and quartz fiber dosimeters.
A variety of units are used to measure various aspects of radiation (Figure \(\PageIndex{6}\)). The SI unit for rate of radioactive decay is the becquerel (Bq), with 1 Bq = 1 disintegration per second. The curie (Ci) and millicurie (mCi) are much larger units and are frequently used in medicine (1 curie = 1 Ci = 3.7 1010 disintegrations per second). The SI unit for measuring radiation dose is the gray (Gy), with 1 Gy = 1 J of energy absorbed per kilogram of tissue. In medical applications, the radiation absorbed dose (rad) is more often used (1 rad = 0.01 Gy; 1 rad results in the absorption of 0.01 J/kg of tissue). The SI unit measuring tissue damage caused by radiation is the sievert (Sv). This takes into account both the energy and the biological effects of the type of radiation involved in the radiation dose. The roentgen equivalent for man (rem) is the unit for radiation damage that is used most frequently in medicine (100 rem = 1 Sv). Note that the tissue damage units (rem or Sv) includes the energy of the radiation dose (rad or Gy) along with a biological factor referred to as the RBE (for relative biological effectiveness) that is an approximate measure of the relative damage done by the radiation. These are related by:
\[\text { number of rems }=\mathrm{RBE} \times \text { number of rads }\]
with RBE approximately 10 for α radiation, 2(+) for protons and neutrons, and 1 for β and γ radiation.
Units of Radiation Measurement
Table \(\PageIndex{1}\) summarizes the units used for measuring radiation.
| Measurement Purpose | Unit | Quantity Measured | Description |
|---|---|---|---|
| activity of source | becquerel (Bq) | radioactive decays or emissions | amount of sample that undergoes 1 decay/second |
| curie (Ci) | amount of sample that undergoes 3.7 1010 decays/second | ||
| absorbed dose | gray (Gy) | energy absorbed per kg of tissue | 1 Gy = 1 J/kg tissue |
| radiation absorbed dose (rad) | 1 rad = 0.01 J/kg tissue | ||
| biologically effective dose | sievert (Sv) | tissue damage | Sv = RBE Gy |
| roentgen equivalent for man (rem) | Rem = RBE rad |
Cobalt-60 (\(t_{1/2} = 5.26~ y\)) is used in cancer therapy since the γ rays it emits can be focused in small areas where the cancer is located. A 5.00-g sample of Co-60 is available for cancer treatment.
- What is its activity in Bq?
- What is its activity in Ci?
Solution
The activity is given by:
\[\text { Activity }=\lambda N=\left(\frac{\ln 2}{t_{1 / 2}}\right) N=\left(\frac{\ln 2}{5.26 \mathrm{y}}\right) \times 5.00 \mathrm{~g}=0.659 \frac{\mathrm{~g}}{\mathrm{y}} \text { of Co }-60 \text { that decay } \nonumber\]
And to convert this to decays per second:
\[\begin{aligned}
& 0.659 \frac{\mathrm{~g}}{\mathrm{y}} \times \frac{1 \mathrm{y}}{365 \mathrm{~d}} \times \frac{1 \mathrm{~d}}{24 \mathrm{~h}} \times \frac{1 \mathrm{~h}}{3600 \mathrm{~s}} \times \frac{1 \mathrm{~mol}}{59.9 \mathrm{~g}} \times \frac{6.02 \times 10^{23} \text { atoms }}{1 \mathrm{~mol}} \times \frac{1 \text { decay }}{1 \text { atom }} \\
& =2.10 \times 10^{14} \frac{\text { decay }}{\mathrm{s}}
\end{aligned} \nonumber\]
- Since \(1 \mathrm{~Bq}=\frac{1 \text { decay }}{\mathrm{s}}\) the activity in Becquerel (Bq) is: \[2.10 \times 10^{14} \frac{\text { decay }}{\mathrm{s}} \times\left(\frac{1 \mathrm{~Bq}}{1 \frac{\text { decay }}{\mathrm{s}}}\right)=2.10 \times 10^{14} \mathrm{~Bq} \nonumber\]
- Since \(1 \mathrm{Ci}=\frac{3.7 \times 10^{11} \text { decay }}{\mathrm{s}}\) the activity in curie (Ci) is: \[2.10 \times 10^{14} \frac{\text { decay }}{\mathrm{s}} \times\left(\frac{1 \mathrm{Ci}}{\frac{3.7 \times 10^{11} \text { decay }}{\mathrm{s}}}\right)=5.7 \times 10^2 \mathrm{Ci}\nonumber \]
Tritium is a radioactive isotope of hydrogen (t1/2 = 12.32 y) that has several uses, including self-powered lighting, in which electrons emitted in tritium radioactive decay cause phosphorus to glow. Its nucleus contains one proton and two neutrons, and the atomic mass of tritium is 3.016 amu. What is the activity of a sample containing 1.00mg of tritium (a) in Bq and (b) in Ci?
- Answer
-
- 3.56 1011 Bq;
- 0.962 Ci
Effects of Long-term Radiation Exposure on the Human Body
The effects of radiation depend on the type, energy, and location of the radiation source, and the length of exposure. As shown in Figure \(\PageIndex{7}\): , the average person is exposed to background radiation, including cosmic rays from the sun and radon from uranium in the ground (see the Chemistry in Everyday Life feature on Radon Exposure); radiation from medical exposure, including CAT scans, radioisotope tests, X-rays, and so on; and small amounts of radiation from other human activities, such as airplane flights (which are bombarded by increased numbers of cosmic rays in the upper atmosphere), radioactivity from consumer products, and a variety of radionuclides that enter our bodies when we breathe (for example, carbon-14) or through the food chain (for example, potassium-40, strontium-90, and iodine-131).
A short-term, sudden dose of a large amount of radiation can cause a wide range of health effects, from changes in blood chemistry to death. Short-term exposure to tens of rems of radiation will likely cause very noticeable symptoms or illness; a dose of about 500 rems is estimated to have a 50% probability of causing the death of the victim within 30 days of exposure. Exposure to radioactive emissions has a cumulative effect on the body during a person’s lifetime, which is another reason why it is important to avoid any unnecessary exposure to radiation. Health effects of short-term exposure to radiation are shown in Table \(\PageIndex{2}\).
| Exposure (rem) | Health Effect | Time to Onset (without treatment) |
|---|---|---|
| 5–10 | changes in blood chemistry | — |
| 50 | nausea | hours |
| 55 | fatigue | — |
| 70 | vomiting | — |
| 75 | hair loss | 2–3 weeks |
| 90 | diarrhea | — |
| 100 | hemorrhage | — |
| 400 | possible death | within 2 months |
| 1000 | destruction of intestinal lining | — |
| internal bleeding | — | |
| death | 1–2 weeks | |
| 2000 | damage to central nervous system | — |
| loss of consciousness; | minutes | |
| death | hours to days |
It is impossible to avoid some exposure to ionizing radiation. We are constantly exposed to background radiation from a variety of natural sources, including cosmic radiation, rocks, medical procedures, consumer products, and even our own atoms. We can minimize our exposure by blocking or shielding the radiation, moving farther from the source, and limiting the time of exposure.
Footnotes
- 2Source: US Environmental Protection Agency


