12.5: Integrated Rate Laws

Learning Objectives

• Explain the form and function of an integrated rate law
• Perform integrated rate law calculations for zero-, first-, and second-order reactions
• Define half-life and carry out related calculations
• Identify the order of a reaction from concentration/time data

The rate laws we have seen thus far relate the rate and the concentrations of reactants. We can also determine a second form of each rate law that relates the concentrations of reactants and time. These are called integrated rate laws. We can use an integrated rate law to determine the amount of reactant or product present after a period of time or to estimate the time required for a reaction to proceed to a certain extent. For example, an integrated rate law is used to determine the length of time a radioactive material must be stored for its radioactivity to decay to a safe level.

Using calculus, the differential rate law for a chemical reaction can be integrated with respect to time to give an equation that relates the amount of reactant or product present in a reaction mixture to the elapsed time of the reaction. This process can either be very straightforward or very complex, depending on the complexity of the differential rate law. For purposes of discussion, we will focus on the resulting integrated rate laws for first-, second-, and zero-order reactions.

First-Order Reactions

An equation relating the rate constant \(k\) to the initial concentration \([A]_0\) and the concentration \([A]_t\) present after any given time \(t\) can be derived for a first-order reaction and shown to be:

\[\ln\left(\dfrac{[A]_t}{[A]_0}\right)=−kt \nonumber \]

or alternatively

\[\ln\left(\dfrac{[A]_0}{[A]_t}\right)=kt \nonumber \]

or

\[[A]=[A]_0e^{−kt} \nonumber \]

Example \(\PageIndex{1}\): The Integrated Rate Law for a First-Order Reaction

The rate constant for the first-order decomposition of cyclobutane, \(\ce{C4H8}\) at 500 °C is 9.2 × 10⁻³ s⁻¹:

\[\ce{C4H8⟶2C2H4} \nonumber \]

How long will it take for 80.0% of a sample of C₄H₈ to decompose?

Solution

We use the integrated form of the rate law to answer questions regarding time:

\[\ln\left(\dfrac{[A]_0}{[A]}\right)=kt \nonumber \]

There are four variables in the rate law, so if we know three of them, we can determine the fourth. In this case we know [A]₀, [A], and k, and need to find t.

The initial concentration of C₄H₈, [A]₀, is not provided, but the provision that 80.0% of the sample has decomposed is enough information to solve this problem. Let x be the initial concentration, in which case the concentration after 80.0% decomposition is 20.0% of x or 0.200x. Rearranging the rate law to isolate t and substituting the provided quantities yields:

\[\begin{align*}
t&=\ln\dfrac{[x]}{[0.200x]}×\dfrac{1}{k}\\[4pt]
&=\mathrm{\ln\dfrac{0.100\:mol\: L^{−1}}{0.020\:mol\: L^{−1}}×\dfrac{1}{9.2×10^{−3}\:s^{−1}}}\\[4pt]
&=\mathrm{1.609×\dfrac{1}{9.2×10^{−3}\:s^{−1}}}\\[4pt]
&=\mathrm{1.7×10^2\:s}
\end{align*} \nonumber \]

Exercise \(\PageIndex{1}\)

Iodine-131 is a radioactive isotope that is used to diagnose and treat some forms of thyroid cancer. Iodine-131 decays to xenon-131 according to the equation:

\[\textrm{I-131 ⟶ Xe-131 + electron} \nonumber \]

The decay is first-order with a rate constant of 0.138 d⁻¹. All radioactive decay is first order. How many days will it take for 90% of the iodine−131 in a 0.500 M solution of this substance to decay to Xe-131?

Answer

16.7 days

We can use integrated rate laws with experimental data that consist of time and concentration information to determine the order and rate constant of a reaction. The integrated rate law can be rearranged to a standard linear equation format:

\[\begin{align}
\ln[A]&=(−k)(t)+\ln[A]_0 \label{in1st}\\[4pt]
y&=mx+b
\end{align} \nonumber \]

A plot of \(\ln[A]\) versus \(t\) for a first-order reaction is a straight line with a slope of \(−k\) and an intercept of \(\ln[A]_0\). If a set of rate data are plotted in this fashion but do not result in a straight line, the reaction is not first order in \(A\).

Example \(\PageIndex{2}\): Determination of Reaction Order by Graphing

Show that the data in this Figure can be represented by a first-order rate law by graphing ln[H₂O₂] versus time. Determine the rate constant for the rate of decomposition of H₂O₂ from this data.

Solution

The data from this Figure with the addition of values of ln[H₂O₂] are given in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): The linear relationship between the ln[H₂O₂] and time shows that the decomposition of hydrogen peroxide is a first-order reaction.

Solutions to Example 12.4.2

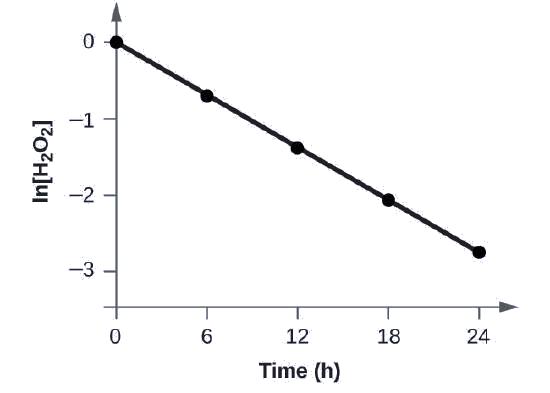
Trial	Time (h)	[H2O2] (M)	ln[H2O2]
1	0	1.000	0.0
2	6.00	0.500	−0.693
3	12.00	0.250	−1.386
4	18.00	0.125	−2.079
5	24.00	0.0625	−2.772

The plot of ln[H₂O₂] versus time is linear, thus we have verified that the reaction may be described by a first-order rate law.

The rate constant for a first-order reaction is equal to the negative of the slope of the plot of ln[H₂O₂] versus time where:

\[\ce{slope}=\dfrac{\textrm{change in }y}{\textrm{change in }x}=\dfrac{Δy}{Δx}=\dfrac{Δ\ln[\ce{H2O2}]}{Δt} \nonumber \]

In order to determine the slope of the line, we need two values of ln[H₂O₂] at different values of t (one near each end of the line is preferable). For example, the value of ln[H₂O₂] when t is 6.00 h is −0.693; the value when t = 12.00 h is −1.386:

\[\begin{align*}
\ce{slope}&=\mathrm{\dfrac{−1.386−(−0.693)}{12.00\: h−6.00\: h}}\\[4pt]
&=\mathrm{\dfrac{−0.693}{6.00\: h}}\\[4pt]
&=\mathrm{−1.155×10^{−2}\:h^{−1}}\\[4pt]
k&=\mathrm{−slope=−(−1.155×10^{−1}\:h^{−1})=1.155×10^{−1}\:h^{−1}}
\end{align*} \nonumber \]

Exercise \(\PageIndex{2}\)

Graph the following data to determine whether the reaction \(A⟶B+C\) is first order.

Data for the reaction \(A⟶B+C\)

Trial	Time (s)	[A]
1	4.0	0.220
2	8.0	0.144
3	12.0	0.110
4	16.0	0.088
5	20.0	0.074

Answer

The plot of ln[A] vs. t is not a straight line. The equation is not first order:

 

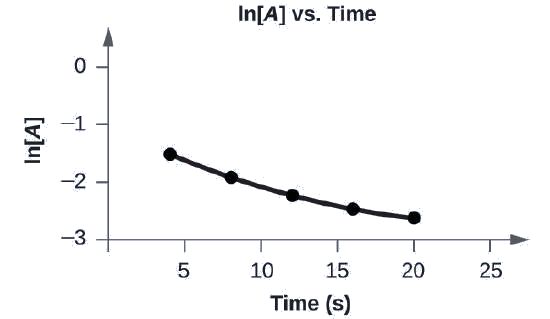
A graph, labeled above as “l n [ A ] vs. Time” is shown. The x-axis is labeled, “Time ( s )” and the y-axis is labeled, “l n [ A ].” The x-axis shows markings at 5, 10, 15, 20, and 25 hours. The y-axis shows markings at negative 3, negative 2, negative 1, and 0. A slight curve is drawn connecting five points at coordinates of approximately (4, negative 1.5), (8, negative 2), (12, negative 2.2), (16, negative 2.4), and (20, negative 2.6).

 

Second-Order Reactions

The equations that relate the concentrations of reactants and the rate constant of second-order reactions are fairly complicated. We will limit ourselves to the simplest second-order reactions, namely, those with rates that are dependent upon just one reactant’s concentration and described by the differential rate law:

\[\ce{Rate}=k[A]^2 \nonumber \]

For these second-order reactions, the integrated rate law is:

\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \label{int2nd} \]

where the terms in the equation have their usual meanings as defined earlier.

Example \(\PageIndex{3}\): The Integrated Rate Law for a Second-Order Reaction

The reaction of butadiene gas (C₄H₆) with itself produces C₈H₁₂ gas as follows:

\[\ce{2C4H6}(g)⟶\ce{C8H12(g)} \nonumber \]

The reaction is second order with a rate constant equal to 5.76 × 10⁻² L/mol/min under certain conditions. If the initial concentration of butadiene is 0.200 M, what is the concentration remaining after 10.0 min?

Solution

We use the integrated form of the rate law to answer questions regarding time. For a second-order reaction, we have:

\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]

We know three variables in this equation: [A]₀ = 0.200 mol/L, k = 5.76 × 10⁻² L/mol/min, and t = 10.0 min. Therefore, we can solve for [A], the fourth variable:

\[\begin{align*}
\dfrac{1}{[A]}&=\mathrm{(5.76×10^{−2}\:L\: mol^{−1}\:min^{−1})(10\:min)+\dfrac{1}{0.200\:mol^{−1}}}\\[4pt]
\dfrac{1}{[A]}&=\mathrm{(5.76×10^{−1}\:L\: mol^{−1})+5.00\:L\: mol^{−1}}\\[4pt]
\dfrac{1}{[A]}&=\mathrm{5.58\:L\: mol^{−1}}\\[4pt]
[A]&=\mathrm{1.79×10^{−1}\:mol\: L^{−1}}
\end{align*} \nonumber \]

Therefore 0.179 mol/L of butadiene remain at the end of 10.0 min, compared to the 0.200 mol/L that was originally present.

Exercise \(\PageIndex{3}\)

If the initial concentration of butadiene is 0.0200 M, what is the concentration remaining after 20.0 min?

Answer

0.0196 mol/L

The integrated rate law for our second-order reactions has the form of the equation of a straight line:

\[\begin{align*}
\dfrac{1}{[A]}&=kt+\dfrac{1}{[A]_0}\\[4pt]
y&=mx+b
\end{align*} \nonumber \]

A plot of \(\dfrac{1}{[A]}\) versus t for a second-order reaction is a straight line with a slope of k and an intercept of \(\dfrac{1}{[A]_0}\). If the plot is not a straight line, then the reaction is not second order.

Example \(\PageIndex{4}\): Determination of Reaction Order by Graphing

Test the data given to show whether the dimerization of C₄H₆ is a first- or a second-order reaction.

Solution

Solutions to Example 12.4.4

Trial	Time (s)	[C4H6] (M)
1	0	1.00 × 10^−2
2	1600	5.04 × 10^−3
3	3200	3.37 × 10^−3
4	4800	2.53 × 10^−3
5	6200	2.08 × 10^−3

In order to distinguish a first-order reaction from a second-order reaction, we plot ln[C₄H₆] versus t and compare it with a plot of \(\mathrm{\dfrac{1}{[C_4H_6]}}\) versus t. The values needed for these plots follow.

Solutions to Example 12.4.4

Time (s)	\(\dfrac{1}{[\ce{C4H6}]}\:(M^{−1})\)	ln[C4H6]
0	100	−4.605
1600	198	−5.289
3200	296	−5.692
4800	395	−5.978
6200	481	−6.175

The plots are shown in Figure \(\PageIndex{2}\). As you can see, the plot of ln[C₄H₆] versus t is not linear, therefore the reaction is not first order. The plot of \(\dfrac{1}{[\ce{C4H6}]}\) versus t is linear, indicating that the reaction is second order.

Figure \(\PageIndex{2}\): These two graphs show first- and second-order plots for the dimerization of C₄H₆. Since the first-order plot (left) is not linear, we know that the reaction is not first order. The linear trend in the second-order plot (right) indicates that the reaction follows second-order kinetics.

Two graphs are shown, each with the label “Time ( s )” on the x-axis. The graph on the left is labeled, “l n [ C subscript 4 H subscript 6 ],” on the y-axis. The graph on the right is labeled “1 divided by [ C subscript 4 H subscript 6 ],” on the y-axis. The x-axes for both graphs show markings at 3000 and 6000. The y-axis for the graph on the left shows markings at negative 6, negative 5, and negative 4. A decreasing slightly concave up curve is drawn through five points at coordinates that are (0, negative 4.605), (1600, negative 5.289), (3200, negative 5.692), (4800, negative 5.978), and (6200, negative 6.175). The y-axis for the graph on the right shows markings at 100, 300, and 500. An approximately linear increasing curve is drawn through five points at coordinates that are (0, 100), (1600, 198), (3200, 296), and (4800, 395), and (6200, 481).

Exercise \(\PageIndex{4}\)

Does the following data fit a second-order rate law?

Data for second-order rate law

Trial	Time (s)	[A] (M)
1	5	0.952
2	10	0.625
3	15	0.465
4	20	0.370
5	25	0.308
6	35	0.230

 

Answer

Yes. The plot of \(\dfrac{1}{[A]}\) vs. t is linear:

 

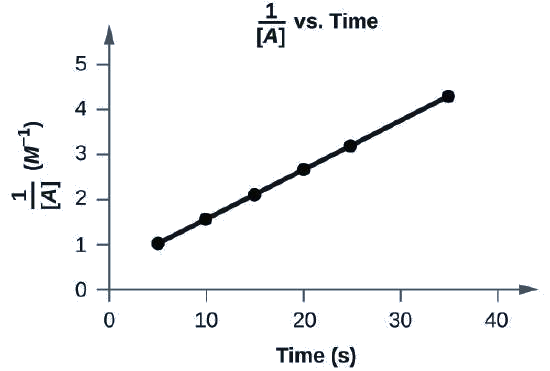
A graph, with the title “1 divided by [ A ] vs. Time” is shown, with the label, “Time ( s ),” on the x-axis. The label “1 divided by [ A ]” appears left of the y-axis. The x-axis shows markings beginning at zero and continuing at intervals of 10 up to and including 40. The y-axis on the left shows markings beginning at 0 and increasing by intervals of 1 up to and including 5. A line with an increasing trend is drawn through six points at approximately (4, 1), (10, 1.5), (15, 2.2), (20, 2.8), (26, 3.4), and (36, 4.4).

 

Zero-Order Reactions

For zero-order reactions, the differential rate law is:

\[\ce{Rate}=k[A]^0=k \nonumber \]

A zero-order reaction thus exhibits a constant reaction rate, regardless of the concentration of its reactants.

The integrated rate law for a zero-order reaction also has the form of the equation of a straight line:

\[\begin{align*}
[A]&=−kt+[A]_0 \label{intzero}\\[4pt]
y&=mx+b
\end{align*} \nonumber \]

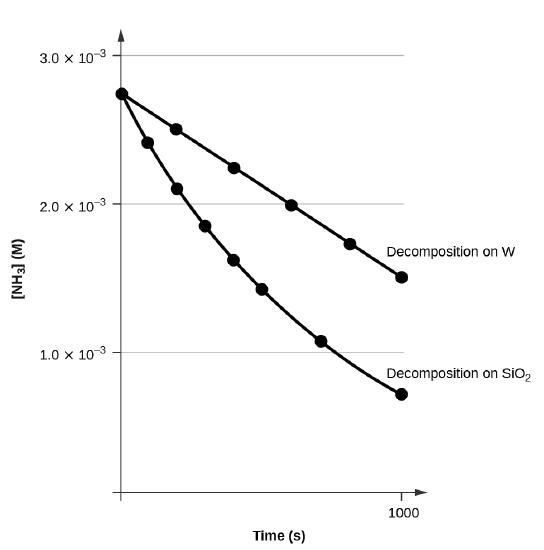
A plot of \([A]\) versus \(t\) for a zero-order reaction is a straight line with a slope of −k and an intercept of [A]₀. Figure \(\PageIndex{3}\) shows a plot of [NH₃] versus t for the decomposition of ammonia on a hot tungsten wire and for the decomposition of ammonia on hot quartz (SiO₂). The decomposition of NH₃ on hot tungsten is zero order; the plot is a straight line. The decomposition of NH₃ on hot quartz is not zero order (it is first order). From the slope of the line for the zero-order decomposition, we can determine the rate constant:

\[\ce{slope}=−k=\mathrm{1.3110^{−6}\:mol/L/s} \nonumber \]

Figure \(\PageIndex{3}\): The decomposition of NH₃ on a tungsten (W) surface is a zero-order reaction, whereas on a quartz (SiO₂) surface, the reaction is first order.

 

The Half-Life of a Reaction

The half-life of a reaction (t_1/2) is the time required for one-half of a given amount of reactant to be consumed. In each succeeding half-life, half of the remaining concentration of the reactant is consumed. Using the decomposition of hydrogen peroxide as an example, we find that during the first half-life (from 0.00 hours to 6.00 hours), the concentration of H₂O₂ decreases from 1.000 M to 0.500 M. During the second half-life (from 6.00 hours to 12.00 hours), it decreases from 0.500 M to 0.250 M; during the third half-life, it decreases from 0.250 M to 0.125 M. The concentration of H₂O₂ decreases by half during each successive period of 6.00 hours. The decomposition of hydrogen peroxide is a first-order reaction, and, as can be shown, the half-life of a first-order reaction is independent of the concentration of the reactant. However, half-lives of reactions with other orders depend on the concentrations of the reactants.

First-Order Reactions

We can derive an equation for determining the half-life of a first-order reaction from the alternate form of the integrated rate law as follows:

\[\begin{align*}
\ln\dfrac{[A]_0}{[A]}&=kt\\[4pt]
t&=\ln\dfrac{[A]_0}{[A]}×\dfrac{1}{k}
\end{align*} \nonumber \]

If we set the time t equal to the half-life, \(t_{1/2}\), the corresponding concentration of A at this time is equal to one-half of its initial concentration. Hence, when \(t=t_{1/2}\), \([A]=\dfrac{1}{2}[A]_0\).

Therefore:

\[\begin{align*}
t_{1/2}&=\ln\dfrac{[A]_0}{\dfrac{1}{2}[A]_0}×\dfrac{1}{k}\\[4pt]
&=\ln 2×\dfrac{1}{k}=0.693×\dfrac{1}{k}
\end{align*} \nonumber \]

Thus:

\[t_{1/2}=\dfrac{0.693}{k} \nonumber \]

We can see that the half-life of a first-order reaction is inversely proportional to the rate constant k. A fast reaction (shorter half-life) will have a larger k; a slow reaction (longer half-life) will have a smaller k.

Example \(\PageIndex{5}\): Calculation of a First-order Rate Constant using Half-Life

Calculate the rate constant for the first-order decomposition of hydrogen peroxide in water at 40 °C, using the data given in Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\): The decomposition of H₂O₂ \(\ce{(2H2O2⟶2H2O + O2)}\) at 40 °C is illustrated. The intensity of the color symbolizes the concentration of H₂O₂ at the indicated times; H₂O₂ is actually colorless.

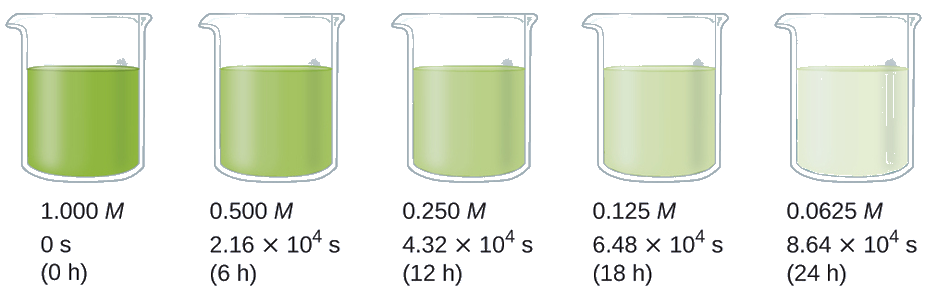
Solution The half-life for the decomposition of H₂O₂ is 2.16 × 10⁴ s:

\[\begin{align*}
t_{1/2}&=\dfrac{0.693}{k}\\[4pt]
k&=\dfrac{0.693}{t_{1/2}}=\dfrac{0.693}{2.16×10^4\:\ce s}=3.21×10^{−5}\:\ce s^{−1}
\end{align*} \nonumber \]

Exercise \(\PageIndex{1}\)

The first-order radioactive decay of iodine-131 exhibits a rate constant of 0.138 d⁻¹. What is the half-life for this decay?

Answer

5.02 d.

 

Second-Order Reactions

We can derive the equation for calculating the half-life of a second order as follows:

\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]

or

\[\dfrac{1}{[A]}−\dfrac{1}{[A]_0}=kt \nonumber \]

If

\[t=t_{1/2} \nonumber \]

then

\[[A]=\dfrac{1}{2}[A]_0 \nonumber \]

and we can write:

\(\begin{align*}
\dfrac{1}{\dfrac{1}{2}[A]_0}−\dfrac{1}{[A]_0}&=kt_{1/2}\\[4pt]
2[A]_0−\dfrac{1}{[A]_0}&=kt_{1/2}\\[4pt]
\dfrac{1}{[A]_0}&=kt_{1/2}
\end{align*}\)

Thus:

\[t_{1/2}=\dfrac{1}{k[A]_0} \nonumber \]

For a second-order reaction, \(t_{1/2}\) is inversely proportional to the concentration of the reactant, and the half-life increases as the reaction proceeds because the concentration of reactant decreases. Consequently, we find the use of the half-life concept to be more complex for second-order reactions than for first-order reactions. Unlike with first-order reactions, the rate constant of a second-order reaction cannot be calculated directly from the half-life unless the initial concentration is known.

 

Zero-Order Reactions

We can derive an equation for calculating the half-life of a zero order reaction as follows:

\[[A]=−kt+[A]_0 \nonumber \]

When half of the initial amount of reactant has been consumed \(t=t_{1/2}\) and \([A]=\dfrac{[A]_0}{2}\). Thus:

\[\begin{align*}
\dfrac{[A]_0}{2}&=−kt_{1/2}+[A]_0\\[4pt]
kt_{1/2}&=\dfrac{[A]_0}{2}
\end{align*} \nonumber \]

and

\[t_{1/2}=\dfrac{[A]_0}{2k} \nonumber \]

The half-life of a zero-order reaction increases as the initial concentration increases. Equations for both differential and integrated rate laws and the corresponding half-lives for zero-, first-, and second-order reactions are summarized in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Summary of Rate Laws for Zero-, First-, and Second-Order Reactions

	Zero-Order	First-Order	Second-Order
rate law	rate = k	rate = k[A]	rate = k[A]^2
units of rate constant	M s^−1	s^−1	M^−1 s^−1
integrated rate law	[A] = −kt + [A]0	ln[A] = −kt + ln[A]0	\(\dfrac{1}{[A]}=kt+\left(\dfrac{1}{[A]_0}\right)\)
plot needed for linear fit of rate data	[A] vs. t	ln[A] vs. t	\(\dfrac{1}{[A]}\) vs. t
relationship between slope of linear plot and rate constant	k = −slope	k = −slope	k = +slope
half-life	\(t_{1/2}=\dfrac{[A]_0}{2k}\)	\(t_{1/2}=\dfrac{0.693}{k}\)	\(t_{1/2}=\dfrac{1}{[A]_0k}\)

 

Summary

Differential rate laws can be determined by the method of initial rates or other methods. We measure values for the initial rates of a reaction at different concentrations of the reactants. From these measurements, we determine the order of the reaction in each reactant. Integrated rate laws are determined by integration of the corresponding differential rate laws. Rate constants for those rate laws are determined from measurements of concentration at various times during a reaction.

The half-life of a reaction is the time required to decrease the amount of a given reactant by one-half. The half-life of a zero-order reaction decreases as the initial concentration of the reactant in the reaction decreases. The half-life of a first-order reaction is independent of concentration, and the half-life of a second-order reaction decreases as the concentration increases.

Key Equations

• integrated rate law for zero-order reactions (Equation \ref{intzero}):

\([A]=−kt+[A]_0\) with \(t_{1/2}=\dfrac{[A]_0}{2k}\)

• integrated rate law for first-order reactions (Equation \ref{in1st}):

\(\ln[A]=−kt+ \ln[A]_0\) with \(t_{1/2}=\dfrac{0.693}{k}\)

• integrated rate law for second-order reactions (Equation \ref{int2nd}):

\(\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}\) with \(t_{1/2}=\dfrac{1}{[A]_0k}\)

Glossary

half-life of a reaction (t_l/2)

time required for half of a given amount of reactant to be consumed

integrated rate law

equation that relates the concentration of a reactant to elapsed time of reaction