5.4.3: Sports, Physiology, and Health- Sea Kayaking and Clapotis
- Page ID
- 50016
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Wave Nature of the Electron in Sports, Physiology & Health
ClapotisOcean kayakers may get unexpectedly tossed in the air by high waves called clapotis[1]. Clapotis arise near to shore where incoming waves hit the shore, and are reflected. The reflected outgoing waves meet incoming waves to give very high wave peaks adjacent to calm regions. This YouTube video shows a clipotis on the Oregon coast, and a still image of the clapotis is shown below. Other videos show similar effects.
Surprisingly, clapotis provide a model for the behavior of electrons confined to a nucleus. Like most models, the clapotis model is flawed, because ocean waves and the shore are irregular. Clapotis therefore arise irregularly (although often in the same position, as careful observation of the videos will show. But electron waves follow a fixed, regular pattern as described below.
If the waves were perfectly sinusoidal and the coastline were perfectly linear, the clapotis would appear constantly at a certain distance from shore, and the distance can be predicted by the wave model shown in a YouTube video, or in the animation below. The animation is a cross section of a wave, but could also be imagined as a wave on a string. The right end is fixed, and the left end is moving up and down. The up-and-down motion creates a "travelling wave" that moves to the right, hits the right end, and is then reflected back towards the left. The waves moving to the right and left interfere to create a "standing wave" pattern, where the crests of the waves don't travel, but are located at points labeled L2 in the animation. Between the crests, there are nodes, or points where there is no motion at all. Somehow the motion appears on both sides of the nodes without any motion at the nodes at all. As you can see in the animation, "constructive interference" occurs when the crests of the two waves arrive at the same point at the same time, reinforcing each other, and producing a resultant crest, or "antinode" which is as high as the sum of the heights of the two waves (this is called the "superposition principle"). If a crest and a trough arrive at the same point at the same time (halfway between L/2 and L/4 in the animation), "destructive interference" occurs, and the superposition principle predicts that they will cancel each other out, giving a node.
Clapotis at wall gif [chemwiki.ucdavis.edu]
A number of discrete, "allowed" standing wave patterns are exhibited by waves on a string. The patterns are slightly different depending on whether the string is fixed or allowed to move at one end. Below are the patterns generated by a string vibrating at different frequencies, but fixed at both ends. The animation shows two "wavelengths" between the ends, corresponding to the 4th pattern from the bottom in the figure on the left.
|
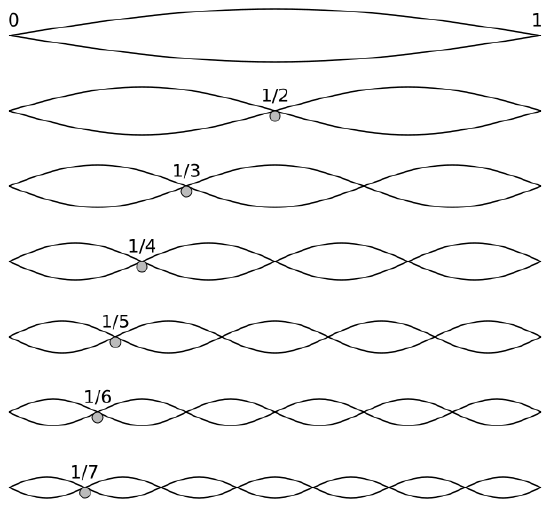
Standing waves on a string
|
Standing wave animation gif [chemwiki.ucdavis.edu] |
But some frequencies are not allowed (we don't want the guitar to play all tones at once!). It happens in situations like this:

This model fits with the counterintuitive behavior of electrons in atoms. Specifically, electrons appear to exist in certain regions of space, but never in regions in between. Furthermore, electrons exist in a series of discrete "orbital" wavefunctions of increasing energy. The energy increases as the number of nodes increases. So the standing wave pattern goes from one node to two nodes, for example, and can't exist anywhere in between. That's exactly the behavior we find for electrons in shells!. Electrons don't exist anywhere between the shells. A standing wave can thus be correlated with electron density in the "orbitals" of an atom, as shown in the figure below. Just as the vibrating string has no fixed position at the antinodes, it is impossible to specify the position (or exact motion) of electrons constrained to a nucleus.
Videos of another standing wave are shown here.
Wavelength and Frequency of Light Waves
Waves are used as a model for light as well, so let's define the wavelength and frequency of a wave a little more precisely. When you flick a string, a traveling wave moves down it; if you do this continually, say once a second, you generate a travelling wave train with a frequency of 1 s-1, or one wavelength per second, where the wavelength is the distance between successive peaks (or any other repeating feature) of the wave:
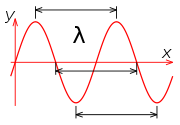
There is a relationship between the frequency, usually denoted "ν" ("nu"), the wavelength, usually denoted "λ" (lambda) and the speed that the wave moves down the string (or through space, if it's a light wave). If we denote the speed "c" (a symbol used for the speed of light), the relationship is:
-
- \(\lambda =\tfrac{c}{\nu} \tag{1}\)
Calculate the wavelength of a microwave in a microwave oven that travels at the speed of light, c = 3.0 x 108 m s-1> and has a frequency of 2.45 GHz (2.45 x 109 s-1. of 12.24 cm.
Solution: Rearranging (1) we have:
-
- \(\nu =\tfrac{c}{\lambda} = \tfrac{\text{3.0}\times \text{10}^{\text{8}}\text{m s}^{\text{-1}}}{\text{2.45}\times\text{10}^{9}\text{s}^{\text{-1}}} = 0.1224 \text{ m or 2.24 cm }\)
Microwaves are waves like light waves or radio waves, but their wavelength is much longer than light, and shorter than radio. Waves of this wavelength interact with water molecules make the molecules spin faster and thereby heat up food in a microwave oven.
Historical Development
At much the same time as Lewis was developing his theories of electronic structure, the physicist Niels Bohr was developing a similar, but more detailed, picture of the atom.
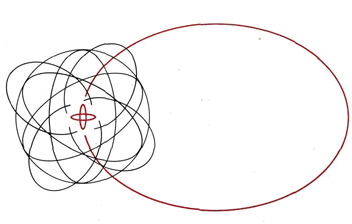
Since Bohr was interested in light (energy) emitted by atoms under certain circumstances rather than the valence of elements, he particularly wanted to be able to calculate the energies of the electrons. To do this, he needed to know the exact path followed by each electron as it moved around the nucleus. He assumed paths similar to those of the planets around the sun. The figure seen here, taken from a physics text of the period, illustrates Bohr’s theories applied to the sodium atom. Note how the Bohr model, like that of Lewis, assumes a shell structure. There are two electrons in the innermost shell, eight electrons in the next shell, and a single electron in the outermost shell.
Like Lewis’ model, Bohr’s model was only partially successful. It explained some experimental results but was quite unable to account for others. In particular it failed on the quantitative mathematical level. The Bohr theory worked very well for a hydrogen atom with its single electron, but calculations on atoms with more than one electron always gave the wrong answer. On a chemical level, too, certain features were inadequate. There is no evidence to suggest that atoms of sodium are ever as elongated or as flat as the one in the figure. On the contrary, the way that sodium atoms pack together in a solid suggests that they extend out uniformly in all directions; i.e., they are spherical in shape. Another weakness in the theory was that it had to assume a shell structure rather than explain it. After all, there is nothing in the nature of planets moving around the sun which compels them to orbit in groups of two or eight. Bohr assumed that electrons behave much like planets; so why should they form shells in this way?
Light Energy
We usually think of electron shells in terms of their energy. That's because light energy is emitted when an electron falls from a higher shell to a lower one, and measuring light energy is the most important way of determining the energy difference between shells. When electrons change levels, they emit quanta of light called "photons"). The energy of a photon is directly related to its frequency, or inversely related to the wavelength:
-
- \(\text{E} = \text {h} \times \nu =\frac{\text{h}\times\text{c}}{\lambda} \tag{2} \)
The constant of proportionality h is known as Planck’s constant and has the value 6.626 × 10–34 J s. Light of higher frequency has higher energy, an a shorter wavelength.
Light can only be absorbed by atoms if each photon has exactly the right amount of energy to promote an electron from a lower shell to a higher one. If more energy is required than a photon possesses, it can't be supplied by bombarding the atom with more photons. So we frequently find that light of one wavelength will cause a photochemical change no matter how dim it is, while light of a neighboring wavelength will not cause a photochemical change no matter how intense it is. That's because photons must be absorbed to cause a photochemical change, and they must have exactly the energy needed to be promoted to the next shell to be absorbed. If they're not absorbed, it doesn't matter how intense the light is (how many photons there are per second).
What wavelength of light is emitted by a hydrogen atom when an electron falls from the third shell, where it has E = -2.42088863 × 10-19J, to the second shell, where it has E = -5.44739997 × 10-19 J?
Solution: ΔE = E2 - E1 = (-5.45 × 10-19) - (-2.42 × 10-19J) = -3.03 × 10-19J. Note that the energy levels get more negative (more energy is released when an electron falls into them) near the nucleus, and the difference here is negative, meaning energy is released. Taking the absolute value of the energy to calculate the energy of the photon, and rearraning equation (2):
-
- \(\lambda =\frac{\text{h}\times\text{c}}{E}\)
- λ = [(6.626 × 10–34 J s)(3 x 108)] / 3.03 × 10-19J = 6.56 x 10-7 m or 656 nm, the wavelength of red light.
Two Dimensional Standing Waves
Of course the shells for electrons are three dimensional, not one dimensional like guitar strings. We can begin to visualize standing waves in more than one dimension by thinking about wave patterns on a drum skin in two dimensions. Some of the wave patterns are shown below. If you look carefully, you'll see circular nodes that don't move:
|
Drum vibration mode 01 gif [chemwiki.ucdavis.edu]  |
Drum vibration mode 02 [chemwiki.ucdavis.edu]  |
Drum vibration mode 03 gif [chemwiki.ucdavis.edu]  |
The Shape of Orbitals
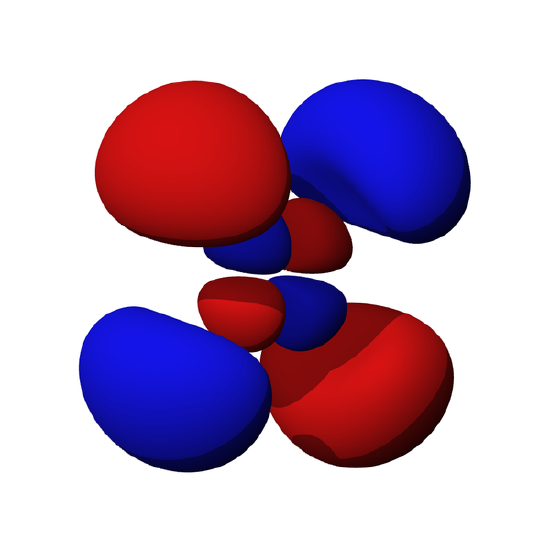
Electrons exist around the nucleus in "orbitals", which are three-dimensional standing waves. Electron standing waves are quite beautiful, and we'll see more of them in the next few sections. One example is the flower like "f orbital" below. Here the red parts of the "wavefunction" represent mathematically positive (upward) parts of the standing wave, while blue parts are mathematically negative (downward) parts:
References
- en.Wikipedia.org/wiki/File:Cl...is_at_wall.gif


