10.6: Stoichiometry Involving Gases
- Page ID
- 349462
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To relate the amount of gas consumed or released in a chemical reaction to the stoichiometry of the reaction.
With the ideal gas law, we can use the relationship between the amounts of gases (in moles) and their volumes (in liters) to calculate the stoichiometry of reactions involving gases, if the pressure and temperature are known. This is important for several reasons. Many reactions that are carried out in the laboratory involve the formation or reaction of a gas, so chemists must be able to quantitatively treat gaseous products and reactants as readily as they quantitatively treat solids or solutions. Furthermore, many, if not most, industrially important reactions are carried out in the gas phase for practical reasons. Gases mix readily, are easily heated or cooled, and can be transferred from one place to another in a manufacturing facility via simple pumps and plumbing. As a chemical engineer said to one of the authors, “Gases always go where you want them to, liquids sometimes do, but solids almost never do.”
Example 10.6.1
Sulfuric acid, the industrial chemical produced in greatest quantity (almost 45 million tons per year in the United States alone), is prepared by the combustion of sulfur in air to give SO2, followed by the reaction of SO2 with O2 in the presence of a catalyst to give SO3, which reacts with water to give H2SO4. The overall chemical equation is as follows:
\[\rm 2S(s)+3O_2(g)+2H_2O(l)\rightarrow 2H_2SO_4(aq) \notag \]
What volume of O2 (in liters) at 22°C and 745 mmHg pressure is required to produce 1.00 ton of H2SO4?
Given: reaction, temperature, pressure, and mass of one product
Asked for: volume of gaseous reactant
Strategy:
A Calculate the number of moles of H2SO4 in 1.00 ton. From the stoichiometric coefficients in the balanced chemical equation, calculate the number of moles of O2 required.
B Use the ideal gas law to determine the volume of O2 required under the given conditions. Be sure that all quantities are expressed in the appropriate units.
Solution:
We can see from the stoichiometry of the reaction that 3/2 mol of O2 is required to produce 1 mol of H2SO4. This is a standard stoichiometry problem of the type presented in Chapter 7, except this problem asks for the volume of one of the reactants (O2) rather than its mass. We proceed exactly as in Chapter 7, using the strategy
mass of H2SO4 → moles H2SO4 → moles O2 → liters O2
A We begin by calculating the number of moles of H2SO4 in 1.00 tn:
\[\rm\dfrac{907.18\times10^3\;g\;H_2SO_4}{(2\times1.008+32.06+4\times16.00)\;g/mol}=9250\;mol\;H_2SO_4 \notag \]
We next calculate the number of moles of O2 required:
\[\rm9250\;mol\;H_2SO_4\times\dfrac{3mol\; O_2}{2mol\;H_2SO_4}=1.389\times10^4\;mol\;O_2 \notag \]
B After converting all quantities to the appropriate units, we can use the ideal gas law to calculate the volume of O2:
\[V=\dfrac{nRT}{P}=\rm\dfrac{1.389\times10^4\;mol\times0.08206\dfrac{L\cdot atm}{mol\cdot K}\times(273+22)\;K}{745\;mmHg\times\dfrac{1\;atm}{760\;mmHg}}=3.43\times10^5\;L \notag \]
The answer means that more than 300,000 L of oxygen gas are needed to produce 1 tn of sulfuric acid. These numbers may give you some appreciation for the magnitude of the engineering and plumbing problems faced in industrial chemistry.
Exercise
In Example 5, we saw that Charles used a balloon containing approximately 31,150 L of H2 for his initial flight in 1783. The hydrogen gas was produced by the reaction of metallic iron with dilute hydrochloric acid according to the following balanced chemical equation:
Fe(s) + 2 HCl(aq) → H2(g) + FeCl2(aq)
How much iron (in kilograms) was needed to produce this volume of H2 if the temperature was 30°C and the atmospheric pressure was 745 mmHg?
Answer: 68.6 kg of Fe (approximately 150 lb)
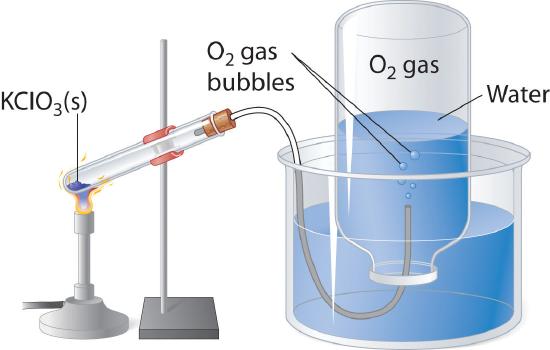
Many of the advances made in chemistry during the 18th and 19th centuries were the result of careful experiments done to determine the identity and quantity of gases produced in chemical reactions. For example, in 1774, Joseph Priestley was able to isolate oxygen gas by the thermal decomposition of mercuric oxide (HgO). In the 1780s, Antoine Lavoisier conducted experiments that showed that combustion reactions, which require oxygen, produce what we now know to be carbon dioxide. Both sets of experiments required the scientists to collect and manipulate gases produced in chemical reactions, and both used a simple technique that is still used in chemical laboratories today: collecting a gas by the displacement of water. As shown in Figure 10.6.1 , the gas produced in a reaction can be channeled through a tube into inverted bottles filled with water. Because the gas is less dense than liquid water, it bubbles to the top of the bottle, displacing the water. Eventually, all the water is forced out and the bottle contains only gas. If a calibrated bottle is used (i.e., one with markings to indicate the volume of the gas) and the bottle is raised or lowered until the level of the water is the same both inside and outside, then the pressure within the bottle will exactly equal the atmospheric pressure measured separately with a barometer.
Figure 10.6.1 An Apparatus for Collecting Gases by the Displacement of Water
When KClO3(s) is heated, O2 is produced according to the equation \[ KClO_{3}\left ( s \right ) \rightarrow KCl\left ( s \right )+\dfrac{3}{2} O_{2}\left ( g \right ) \notag \]. The oxygen gas travels through the tube, bubbles up through the water, and is collected in a bottle as shown.
The only gases that cannot be collected using this technique are those that readily dissolve in water (e.g., NH3, H2S, and CO2) and those that react rapidly with water (such as F2 and NO2). Remember, however, when calculating the amount of gas formed in the reaction, the gas collected inside the bottle is not pure. Instead, it is a mixture of the product gas and water vapor. As we will discuss in Chapter 11 , all liquids (including water) have a measurable amount of vapor in equilibrium with the liquid because molecules of the liquid are continuously escaping from the liquid’s surface, while other molecules from the vapor phase collide with the surface and return to the liquid. The vapor thus exerts a pressure above the liquid, which is called the liquid’s vapor pressure. In the case shown in Figure 10.6.1 the bottle is therefore actually filled with a mixture of O2 and water vapor, and the total pressure is, by Dalton’s law of partial pressures, the sum of the pressures of the two components:
\[P_{\rm tot}=P_{\rm gas}+P_{\rm H_2O}=P_{\rm bar.} \tag{10.6.1}\]
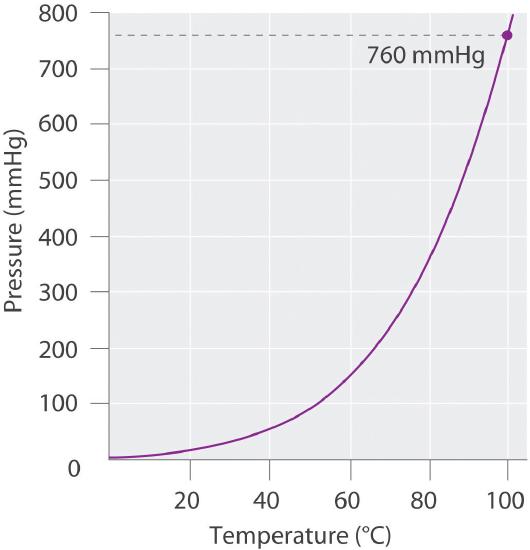
If we want to know the pressure of the gas generated in the reaction to calculate the amount of gas formed, we must first subtract the pressure due to water vapor from the total pressure. This is done by referring to tabulated values of the vapor pressure of water as a function of temperature (Table 10.6.1 ). As shown in Figure 10.6.2, the vapor pressure of water increases rapidly with increasing temperature, and at the normal boiling point (100°C), the vapor pressure is exactly 1 atm. The methodology is illustrated in Example 14.
Table 10.6.1 Vapor Pressure of Water at Various Temperatures
| T (°C) | P (in mmHg) | T | P | T | P | T | P |
|---|---|---|---|---|---|---|---|
| 0 | 4.58 | 21 | 18.66 | 35 | 42.2 | 92 | 567.2 |
| 5 | 6.54 | 22 | 19.84 | 40 | 55.4 | 94 | 611.0 |
| 10 | 9.21 | 23 | 21.08 | 45 | 71.9 | 96 | 657.7 |
| 12 | 10.52 | 24 | 22.39 | 50 | 92.6 | 98 | 707.3 |
| 14 | 11.99 | 25 | 23.77 | 55 | 118.1 | 100 | 760.0 |
| 16 | 13.64 | 26 | 25.22 | 60 | 149.5 | 102 | 815.8 |
| 17 | 14.54 | 27 | 26.75 | 65 | 187.7 | 104 | 875.1 |
| 18 | 15.48 | 28 | 28.37 | 70 | 233.8 | 106 | 937.8 |
| 19 | 16.48 | 29 | 30.06 | 80 | 355.3 | 108 | 1004.2 |
| 20 | 17.54 | 30 | 31.84 | 90 | 525.9 | 110 | 1074.4 |
Figure 10.6.2 A Plot of the Vapor Pressure of Water versus Temperature.
The vapor pressure is very low (but not zero) at 0°C and reaches 1 atm = 760 mmHg at the normal boiling point, 100°C.
Example 10.6.2
Sodium azide (NaN3) decomposes to form sodium metal and nitrogen gas according to the following balanced chemical equation:
\[ 2NaN_3 \rightarrow 2Na_{(s)} + 3N_{2\; (g)} \notag \]
This reaction is used to inflate the air bags that cushion passengers during automobile collisions. The reaction is initiated in air bags by an electrical impulse and results in the rapid evolution of gas. If the N2 gas that results from the decomposition of a 5.00 g sample of NaN3 could be collected by displacing water from an inverted flask, as in Figure 10.6.1, what volume of gas would be produced at 22°C and 762 mmHg?
Given: reaction, mass of compound, temperature, and pressure
Asked for: volume of nitrogen gas produced
Strategy:
A Calculate the number of moles of N2 gas produced. From the data in Table 10.6.1, determine the partial pressure of N2 gas in the flask.
B Use the ideal gas law to find the volume of N2 gas produced.
Solution:
A Because we know the mass of the reactant and the stoichiometry of the reaction, our first step is to calculate the number of moles of N2 gas produced:
[\rm\dfrac{5.00\;g\;NaN_3}{(22.99+3\times14.01)\;g/mol}\times\dfrac{3mol\;N_2}{2mol\;NaN_3}=0.115\;mol\; N_2 \notag \]
The pressure given (762 mmHg) is the total pressure in the flask, which is the sum of the pressures due to the N2 gas and the water vapor present. Table 10.6.1 tells us that the vapor pressure of water is 19.84 mmHg at 22°C (295 K), so the partial pressure of the N2 gas in the flask is only 762 − 19.84 = 742 mmHg = 0.976 atm.
B Solving the ideal gas law for V and substituting the other quantities (in the appropriate units), we get
\[V=\dfrac{nRT}{P}=\rm\dfrac{0.115\;mol\times0.08206\dfrac{atm\cdot L}{mol\cdot K}\times294\;K}{0.978\;atm}=2.84\;L \notag \]
Exercise
A 1.00 g sample of zinc metal is added to a solution of dilute hydrochloric acid. It dissolves to produce H2 gas according to the equation Zn(s) + 2 HCl(aq) → H2(g) + ZnCl2(aq). The resulting H2 gas is collected in a water-filled bottle at 30°C and an atmospheric pressure of 760 mmHg. What volume does it occupy?
Answer: 0.397 L
Summary
The relationship between the amounts of products and reactants in a chemical reaction can be expressed in units of moles or masses of pure substances, of volumes of solutions, or of volumes of gaseous substances. The ideal gas law can be used to calculate the volume of gaseous products or reactants as needed. In the laboratory, gases produced in a reaction are often collected by the displacement of water from filled vessels; the amount of gas can then be calculated from the volume of water displaced and the atmospheric pressure. A gas collected in such a way is not pure, however, but contains a significant amount of water vapor. The measured pressure must therefore be corrected for the vapor pressure of water, which depends strongly on the temperature.
Key Takeaway
- The ideal gas equation and the stoichiometry of a reaction can be used to calculate the volume of gas produced or consumed in a reaction.
Conceptual Problems
-
Why are so many industrially important reactions carried out in the gas phase?
-
The volume of gas produced during a chemical reaction can be measured by collecting the gas in an inverted container filled with water. The gas forces water out of the container, and the volume of liquid displaced is a measure of the volume of gas. What additional information must be considered to determine the number of moles of gas produced? The volume of some gases cannot be measured using this method. What property of a gas precludes the use of this method?
-
Equal masses of two solid compounds (A and B) are placed in separate sealed flasks filled with air at 1 atm and heated to 50°C for 10 hours. After cooling to room temperature, the pressure in the flask containing A was 1.5 atm. In contrast, the pressure in the flask containing B was 0.87 atm. Suggest an explanation for these observations. Would the masses of samples A and B still be equal after the experiment? Why or why not?
Numerical Problems
-
Balance each chemical equation and then determine the volume of the indicated reactant at STP that is required for complete reaction. Assuming complete reaction, what is the volume of the products?
- SO2(g) + O2(g) → SO3(g) given 2.4 mol of O2
- H2(g) + Cl2(g) → HCl(g) given 0.78 g of H2
- C2H6(g) + O2(g) → CO2(g) + H2O(g) given 1.91 mol of O2
-
During the smelting of iron, carbon reacts with oxygen to produce carbon monoxide, which then reacts with iron(III) oxide to produce iron metal and carbon dioxide. If 1.82 L of CO2 at STP is produced,
- what mass of CO is consumed?
- what volume of CO at STP is consumed?
- how much O2 (in liters) at STP is used?
- what mass of carbon is consumed?
- how much iron metal (in grams) is produced?
-
Complete decomposition of a sample of potassium chlorate produced 1.34 g of potassium chloride and oxygen gas.
- What is the mass of KClO3 in the original sample?
- What mass of oxygen is produced?
- What is the volume of oxygen produced at STP?
-
The combustion of a 100.0 mg sample of an herbicide in excess oxygen produced 83.16 mL of CO2 and 72.9 mL of H2O vapor at STP. A separate analysis showed that the sample contained 16.44 mg of chlorine. If the sample is known to contain only C, H, Cl, and N, determine the percent composition and the empirical formula of the herbicide.
-
The combustion of a 300.0 mg sample of an antidepressant in excess oxygen produced 326 mL of CO2 and 164 mL of H2O vapor at STP. A separate analysis showed that the sample contained 23.28% oxygen. If the sample is known to contain only C, H, O, and N, determine the percent composition and the empirical formula of the antidepressant.
Answers
-
- 2.20 g KClO3
- 0.863 g O2
- 604 mL O2
-
Percent composition: 58.3% C, 4.93% H, 23.28% O, and 13.5% N; empirical formula: C10H10O3N2
Contributors
- Anonymous
Modified by Joshua Halpern