10.7: The Kinetic Theory of Gases
- Page ID
- 349463
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To understand the significance of the kinetic molecular theory of gases.
The laws that describe the behavior of gases were well established long before anyone had developed a coherent model of the properties of gases. In this section, we introduce a theory that describes why gases behave the way they do. The theory we introduce can also be used to derive laws such as the ideal gas law from fundamental principles and the properties of individual particles.
A Molecular Description
The kinetic molecular theory of gasesA theory that describes, on the molecular level, why ideal gases behave the way they do. explains the laws that describe the behavior of gases. Developed during the mid-19th century by several physicists, including the Austrian Ludwig Boltzmann (1844–1906), the German Rudolf Clausius (1822–1888), and the Englishman James Clerk Maxwell (1831–1879), who is also known for his contributions to electricity and magnetism, this theory is based on the properties of individual particles as defined for an ideal gas and the fundamental concepts of physics. Thus the kinetic molecular theory of gases provides a molecular explanation for observations that led to the development of the ideal gas law. The kinetic molecular theory of gases is based on the following five postulates:
- A gas is composed of a large number of particles called molecules (whether monatomic or polyatomic) that are in constant random motion.
- Because the distance between gas molecules is much greater than the size of the molecules, the volume of the molecules is negligible.
- Intermolecular interactions, whether repulsive or attractive, are so weak that they are also negligible.
- Gas molecules collide with one another and with the walls of the container, but these collisions are perfectly elastic; that is, they do not change the average kinetic energy of the molecules.
- The average kinetic energy of the molecules of any gas depends on only the temperature, and at a given temperature, all gaseous molecules have exactly the same average kinetic energy.
Although the molecules of real gases have nonzero volumes and exert both attractive and repulsive forces on one another, for the moment we will focus on how the kinetic molecular theory of gases relates to the properties of ideal gases.
Postulates 1 and 4 state that gas molecules are in constant motion and collide frequently with the walls of their containers. The collision of molecules with their container walls results in a momentum transfer (impulse) from molecules to the walls (Figure 10.7.1).
Figure 10.7.1 Momentum transfer (Impulse) from a molecule to the container wall as it bounces off the wall.
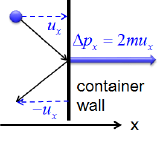
\(u_x\) and \(\Delta p_x\) are the \(x\) component of the molecular velocity and the momentum transfered to the wall, respectively. The wall is perpendicular to \(x\) axis. Since the collisions are elastic, the molecule bounces back with the same velocity in the opposite direction.
The momentum transfer to the wall perpendicular to \(x\) axis as a molecule with an initial velocity \(u_x\) in \(x\) direction hits is expressed as:
\[\Delta p_x=2mu_x \tag{10.7.1} \]
The collision frequency, a number of collisions of the molecules to the wall per unit area and per second, increases with the molecular speed and the number of molecules per unit volume.
\[f\propto (u_x) \times \Big(\dfrac{N}{V}\Big) \tag{10.7.2}\]
The pressure the gas exerts on the wall is expressed as the product of impulse and the collision frequency.
\[P\propto (2mu_x)\times(u_x)\times\Big(\dfrac{N}{V}\Big)\propto \Big(\dfrac{N}{V}\Big)mu_x^2 \tag{10.7.3}\]
At any instant, however, the molecules in a gas sample are traveling at different speed. Therefore, we must replace \(u_x^2\) in the expression above with the average value of \(u_x^2\), which is denoted by \(\overline{u_x^2}\). The overbar designates the average value over all molecules.
The exact expression for pressure is given as :
\[P=\dfrac{N}{V}m\overline{u_x^2} \tag{10.7.4}\]
Finally, we must consider that there is nothing special about \(x\) direction. We should expect that \(\overline{u_x^2}= \overline{u_y^2}=\overline{u_z^2}=\dfrac{1}{3}\overline{u^2}\). Here the quantity \(\overline{u^2}\) is called the mean-square speed defined as the average value of square-speed (\(u^2\)) over all molecules. Since \(u^2=u_x^2+u_y^2+u_z^2\) for each molecule, \(\overline{u^2}=\overline{u_x^2}+\overline{u_y^2}+\overline{u_z^2}\). By substituting \(\dfrac{1}{3}\overline{u^2}\) for \(\overline{u_x^2}\) in the expression above, we can get the final expression for the pressure:
\[P=\dfrac{1}{3}\dfrac{N}{V}m\overline{u^2} \tag{10.7.5}\]
Anything that increases the frequency with which the molecules strike the walls or increases the momentum of the gas molecules (i.e., how hard they hit the walls) increases the pressure; anything that decreases that frequency or the momentum of the molecules decreases the pressure.
Because volumes and intermolecular interactions are negligible, postulates 2 and 3 state that all gaseous particles behave identically, regardless of the chemical nature of their component molecules. This is the essence of the ideal gas law, which treats all gases as collections of particles that are identical in all respects except mass. Postulate 2 also explains why it is relatively easy to compress a gas; you simply decrease the distance between the gas molecules.
Postulate 5 provides a molecular explanation for the temperature of a gas. It refers to the average translational kinetic energy of the molecules of a gas which can be represented as \((\overline{e_K})\), and states that at a given Kelvin temperature \((T)\), all gases have the same value of
\[\overline{e_K}=\dfrac{1}{2}m\overline{u^2}=\dfrac{3}{2}\dfrac{R}{N_A}T \tag{10.7.6}\]
where \(N_A\) is the Avogadro's constant. The total translational kinetic energy of 1 mole of molecules can be obtained by multiplying the equation by \(N_A\):
\[N_A\overline{e_K}=\dfrac{1}{2}M\overline{u^2}=\dfrac{3}{2}RT \tag{10.7.7}\]
where \(M\) is the molar mass of the gas molecules and is related to the molecular mass by \(M=N_Am\).
By rearranging the equation, we can get the relationship between the root-mean square speed (\(u_{\rm rms}\)) and the temperature.
The rms speed (\(u_{\rm rms}\)) is the square root of the sum of the squared speeds divided by the number of particles:
\[u_{\rm rms}=\sqrt{\overline{u^2}}=\sqrt{\dfrac{u_1^2+u_2^2+\cdots u_N^2}{N}} \tag{10.7.8}\]
where \(N\) is the number of particles and \(u_i\) is the speed of particle \(i\).
The relationship between \(u_{\rm rms}\) and the temperature is given by:
\[u_{\rm rms}=\sqrt{\dfrac{3RT}{M}} \tag{10.7.9}\]
In this equation, \(u_{\rm rms}\) has units of meters per second; consequently, the units of molar mass \(M\) are kilograms per mole, temperature \(T\) is expressed in kelvins, and the ideal gas constant \(R\) has the value 8.3145 J/(K·mol).
The equation shows that \(u_{\rm rms}\) of a gas is proportional to the square root of its Kelvin temperature and inversely proportional to the square root of its molar mass. The root mean-square speed of a gas increase with increasing temperature. At a given temperature, heavier gas molecules have slower speeds than do lighter ones.
The rms speed and the average speed do not differ greatly (typically by less than 10%). The distinction is important, however, because the rms speed is the speed of a gas particle that has average kinetic energy. Particles of different gases at the same temperature have the same average kinetic energy, not the same average speed. In contrast, the most probable speed (vp) is the speed at which the greatest number of particles is moving. If the average kinetic energy of the particles of a gas increases linearly with increasing temperature, then Equation 6.33 tells us that the rms speed must also increase with temperature because the mass of the particles is constant. At higher temperatures, therefore, the molecules of a gas move more rapidly than at lower temperatures, and vp increases.
The rms speed and the average speed do not differ greatly (typically by less than 10%). The distinction is important, however, because the rms speed is the speed of a gas particle that has average kinetic energy. Particles of different gases at the same temperature have the same average kinetic energy, not the same average speed. In contrast, the most probable speed (vp) is the speed at which the greatest number of particles is moving. If the average kinetic energy of the particles of a gas increases linearly with increasing temperature, then Equation 10.33 tells us that the rms speed must also increase with temperature because the mass of the particles is constant. At higher temperatures, therefore, the molecules of a gas move more rapidly than at lower temperatures, and vp increases.
Note the Pattern
At a given temperature, all gaseous particles have the same average kinetic energy but not the same average speed.
Example 10.7.1
The speeds of eight particles were found to be 1.0, 4.0, 4.0, 6.0, 6.0, 6.0, 8.0, and 10.0 m/s. Calculate their average speed (\(v_{\rm av}\)) root mean square speed (vrms), and most probable speed (vp).
Given: particle speeds
Asked for: average speed (\(v_{\rm av}\)) root mean square speed (vrms), and most probable speed (vp)
Strategy:
Use Equation 10.7.9 to calculate the average speed and Equation 10.7.8 to calculate the rms speed. Find the most probable speed by determining the speed at which the greatest number of particles is moving.
Solution:
The average speed is the sum of the speeds divided by the number of particles:
\[v_{\rm av}=\rm\dfrac{(1.0+4.0+4.0+6.0+6.0+6.0+8.0+10.0)\;m/s}{8}=5.6\;m/s \notag \]
The rms speed is the square root of the sum of the squared speeds divided by the number of particles:
\[v_{\rm rms}=\rm\sqrt{\dfrac{(1.0^2+4.0^2+4.0^2+6.0^2+6.0^2+6.0^2+8.0^2+10.0^2)\;m^2/s^2}{8}}=6.2\;m/s \notag \]
The most probable speed is the speed at which the greatest number of particles is moving. Of the eight particles, three have speeds of 6.0 m/s, two have speeds of 4.0 m/s, and the other three particles have different speeds. Hence vp = 6.0 m/s. The vrms of the particles, which is related to the average kinetic energy, is greater than their average speed.
Exercise
Ten particles were found to have speeds of 0.1, 1.0, 2.0, 3.0, 3.0, 3.0, 4.0, 4.0, 5.0, and 6.0 m/s. Calculate their average speed (\(v_{\rm av}\)) root mean square speed (vrms), and most probable speed (vp).
Answer: \[ \bar{v} = 3.1 \; m/s;\; v_{rms}=3.5 \; m/s; v_{p}=3.0 m/s \notag \]
Boltzmann Distributions
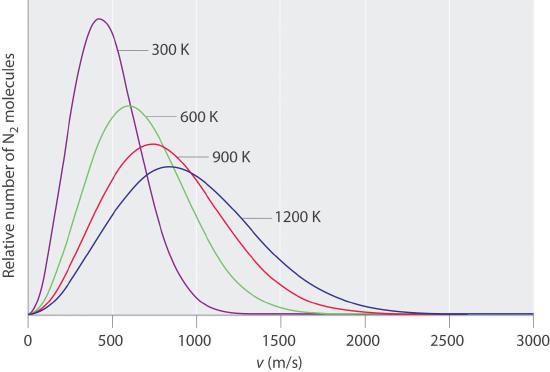
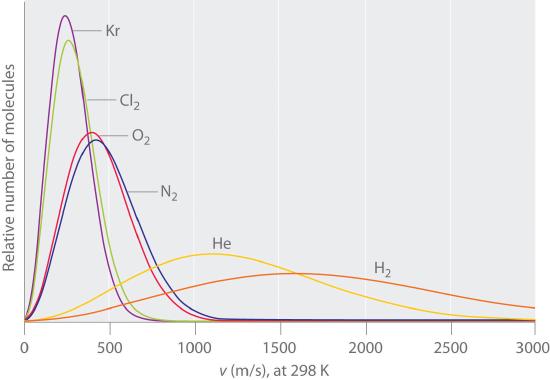
At any given time, what fraction of the molecules in a particular sample has a given speed? Some of the molecules will be moving more slowly than average, and some will be moving faster than average, but how many in each situation? Answers to questions such as these can have a substantial effect on the amount of product formed during a chemical reaction, as you will learn in Chapter 14. This problem was solved mathematically by Maxwell in 1866; he used statistical analysis to obtain an equation that describes the distribution of molecular speeds at a given temperature. Typical curves showing the distributions of speeds of molecules at several temperatures are displayed in Figure 10.7.2 . Increasing the temperature has two effects. First, the peak of the curve moves to the right because the most probable speed increases. Second, the curve becomes broader because of the increased spread of the speeds. Thus increased temperature increases the value of the most probable speed but decreases the relative number of molecules that have that speed. Although the mathematics behind curves such as those in Figure 10.7.2 were first worked out by Maxwell, the curves are almost universally referred to as Boltzmann distributionsA curve that shows the distribution of molecular speeds at a given temperature., after one of the other major figures responsible for the kinetic molecular theory of gases.
Figure 10.7.2 The Distributions of Molecular Speeds for a Sample of Nitrogen Gas at Various Temperature.
Increasing the temperature increases both the most probable speed (given at the peak of the curve) and the width of the curve.
The Relationships among Pressure, Volume, and Temperature
We now describe how the kinetic molecular theory of gases explains some of the important relationships we have discussed previously.
Pressure versus Volume
At constant temperature, the kinetic energy of the molecules of a gas and hence the rms speed remain unchanged. If a given gas sample is allowed to occupy a larger volume, then the speed of the molecules does not change, but the density of the gas (number of particles per unit volume) decreases, and the average distance between the molecules increases. Hence the molecules must, on average, travel farther between collisions. They therefore collide with one another and with the walls of their containers less often, leading to a decrease in pressure. Conversely, increasing the pressure forces the molecules closer together and increases the density, until the collective impact of the collisions of the molecules with the container walls just balances the applied pressure.
Volume versus Temperature
Raising the temperature of a gas increases the average kinetic energy and therefore the rms speed (and the average speed) of the gas molecules. Hence as the temperature increases, the molecules collide with the walls of their containers more frequently and with greater force. This increases the pressure, unless the volume increases to reduce the pressure, as we have just seen. Thus an increase in temperature must be offset by an increase in volume for the net impact (pressure) of the gas molecules on the container walls to remain unchanged.
Pressure of Gas Mixtures
Postulate 3 of the kinetic molecular theory of gases states that gas molecules exert no attractive or repulsive forces on one another. If the gaseous molecules do not interact, then the presence of one gas in a gas mixture will have no effect on the pressure exerted by another, and Dalton’s law of partial pressures holds.
Example 10.7.2
The temperature of a 4.75 L container of N2 gas is increased from 0°C to 117°C. What is the qualitative effect of this change on the
- average kinetic energy of the N2 molecules?
- rms speed of the N2 molecules?
- average speed of the N2 molecules?
- impact of each N2 molecule on the wall of the container during a collision with the wall?
- total number of collisions per second of N2 molecules with the walls of the entire container?
- number of collisions per second of N2 molecules with each square centimeter of the container wall?
- pressure of the N2 gas?
Given: temperatures and volume
Asked for: effect of increase in temperature
Strategy:
Use the relationships among pressure, volume, and temperature to predict the qualitative effect of an increase in the temperature of the gas.
Solution:
- Increasing the temperature increases the average kinetic energy of the N2 molecules.
- An increase in average kinetic energy can be due only to an increase in the rms speed of the gas particles.
- If the rms speed of the N2 molecules increases, the average speed also increases.
- If, on average, the particles are moving faster, then they strike the container walls with more energy.
- Because the particles are moving faster, they collide with the walls of the container more often per unit time.
- The number of collisions per second of N2 molecules with each square centimeter of container wall increases because the total number of collisions has increased, but the volume occupied by the gas and hence the total area of the walls are unchanged.
- The pressure exerted by the N2 gas increases when the temperature is increased at constant volume, as predicted by the ideal gas law.
Exercise
A sample of helium gas is confined in a cylinder with a gas-tight sliding piston. The initial volume is 1.34 L, and the temperature is 22°C. The piston is moved to allow the gas to expand to 2.12 L at constant temperature. What is the qualitative effect of this change on the
- average kinetic energy of the He atoms?
- rms speed of the He atoms?
- average speed of the He atoms?
- impact of each He atom on the wall of the container during a collision with the wall?
- total number of collisions per second of He atoms with the walls of the entire container?
- number of collisions per second of He atoms with each square centimeter of the container wall?
- pressure of the He gas?
Answer: a. no change; b. no change; c. no change; d. no change; e. decreases; f. decreases; g. decreases
Diffusion and Effusion
As you have learned, the molecules of a gas are not stationary but in constant motion. If someone opens a bottle of perfume in the next room, for example, you are likely to be aware of it soon. Your sense of smell relies on molecules of the aromatic substance coming into contact with specialized olfactory cells in your nasal passages, which contain specific receptors (protein molecules) that recognize the substance. How do the molecules responsible for the aroma get from the perfume bottle to your nose? You might think that they are blown by drafts, but, in fact, molecules can move from one place to another even in a draft-free environment. Figure 10.7.3 shows white fumes of solid ammonium chloride (NH4Cl) forming when containers of aqueous ammonia and HCl are placed near each other, even with no draft to stir the air. This phenomenon suggests that NH3 and HCl molecules (as well as the more complex organic molecules responsible for the aromas of pizza and perfumes) move without assistance.
Figure 10.7.3 The Diffusion of Gaseous Molecules.
<
When open containers of aqueous NH3 and HCl are placed near each other in a draft-free environment, molecules of the two substances diffuse, collide, and react to produce white fumes of solid ammonium chloride (NH4Cl). (From the Backyard Scientist)
DiffusionThe gradual mixing of gases due to the motion of their component particles even in the absence of mechanical agitation such as stirring. The result is a gas mixture with a uniform composition. is the gradual mixing of gases due to the motion of their component particles even in the absence of mechanical agitation such as stirring. The result is a gas mixture with uniform composition. As we shall see in Chapter 11 , Chapter 12 , and Chapter 13 , diffusion is also a property of the particles in liquids and liquid solutions and, to a lesser extent, of solids and solid solutions. We can describe the phenomenon shown in Figure 10.7.3 by saying that the molecules of HCl and NH3 are able to diffuse away from their containers, and that NH4Cl is formed where the two gases come into contact. Similarly, we say that a perfume or an aroma diffuses throughout a room or a house. The related process, effusionThe escape of a gas through a small (usually microscopic) opening into an evacuated space., is the escape of gaseous molecules through a small (usually microscopic) hole, such as a hole in a balloon, into an evacuated space.
The phenomenon of effusion had been known for thousands of years, but it was not until the early 19th century that quantitative experiments related the rate of effusion to molecular properties. The rate of effusion of a gaseous substance is inversely proportional to the square root of its molar mass. This relationship, \[ rate\propto \dfrac{1}{\sqrt{M}} \notag \] is referred to as Graham’s lawA law that states that the rate of effusion of a gaseous substance is inversely proportional to the square root of its molar mass., after the Scottish chemist Thomas Graham (1805–1869). The ratio of the effusion rates of two gases is the square root of the inverse ratio of their molar masses. If r is the effusion rate and M is the molar mass, then
\[ \dfrac{r_{1}}{r_{2}}=\dfrac{\sqrt{M_{2}}}{\sqrt{M_{1}}} \tag{10.7.10} \]
Although diffusion and effusion are different phenomena, the rate of diffusion is closely approximated using Equation 10.7.10 that is, if M1 < M2, then gas #1 will diffuse more rapidly than gas #2. This point is illustrated by the experiment shown in Figure 10.7.4 , which is a more quantitative version of the case shown in Figure 10.7.3 . The reaction is the same [NH3(aq) + HCl(aq) → NH4Cl(g)], but in this experiment, two cotton balls containing aqueous ammonia and HCl are placed along a meter stick in a draft-free environment, and the position at which the initial NH4Cl fumes appear is noted. The white cloud forms much nearer the HCl-containing ball than the NH3-containing ball. Because ammonia (M = 17.0 g/mol) diffuses much faster than HCl (M = 36.5 g/mol), the NH4Cl fumes form closer to HCl because the HCl molecules travel a shorter distance. The ratio of the distances traveled by NH3 and HCl in is about 1.7, in reasonable agreement with the ratio of 1.47 predicted by their molar masses [(36.5/17.0)1/2 = 1.47].
Figure 10.7.4 A Simple Experiment to Measure the Relative Rates of the Diffusion of Two Gases
Cotton balls containing aqueous NH3 (left) and HCl (right) are placed a measured distance apart in a draft-free environment, and the position at which white fumes of NH4Cl first appear is noted. The puff of white NH4Cl forms much closer to the HCl-containing ball than to the NH3-containing ball. The left edge of the white puff marks where the reaction was first observed. The position of the white puff (18.8 − 3.3 = 15.5 cm from the NH3, 28.0 − 18.8 = 9.2 cm from the HCl, giving a ratio of distances of 15.5/9.2 = 1.7) is approximately the location predicted by Graham’s law based on the square root of the inverse ratio of the molar masses of the reactants (1.47).
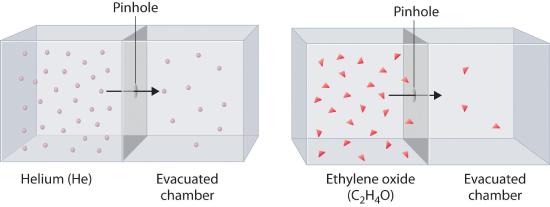
Heavy molecules effuse through a porous material more slowly than light molecules, as illustrated schematically in Figure 10.7.5for ethylene oxide and helium. Helium (M = 4.00 g/mol) effuses much more rapidly than ethylene oxide (M = 44.0 g/mol). Because helium is less dense than air, helium-filled balloons “float” at the end of a tethering string. Unfortunately, rubber balloons filled with helium soon lose their buoyancy along with much of their volume. In contrast, rubber balloons filled with air tend to retain their shape and volume for a much longer time. Because helium has a molar mass of 4.00 g/mol, whereas air has an average molar mass of about 29 g/mol, pure helium effuses through the microscopic pores in the rubber balloon \[ \sqrt{\dfrac{29}{4.00}}=2.7 \notag \] times faster than air. For this reason, high-quality helium-filled balloons are usually made of Mylar, a dense, strong, opaque material with a high molecular mass that forms films that have many fewer pores than rubber. Mylar balloons can retain their helium for days.
Figure 10.7.5 The Relative Rates of Effusion of Two Gases with Different Masses
The lighter He atoms (M = 4.00 g/mol) effuse through the small hole more rapidly than the heavier ethylene oxide (C2H4O) molecules (M = 44.0 g/mol), as predicted by Graham’s law.
Note the Pattern
At a given temperature, heavier molecules move more slowly than lighter molecules.
Example 10.7.3
During World War II, scientists working on the first atomic bomb were faced with the challenge of finding a way to obtain large amounts of 235U. Naturally occurring uranium is only 0.720% 235U, whereas most of the rest (99.275%) is 238U, which is not fissionable (i.e., it will not break apart to release nuclear energy) and also actually poisons the fission process. Because both isotopes of uranium have the same reactivity, they cannot be separated chemically. Instead, a process of gaseous effusion was developed using the volatile compound UF6 (boiling point = 56°C).
- Calculate the ratio of the rates of effusion of 235UF6 and 238UF6 for a single step in which UF6 is allowed to pass through a porous barrier. (The atomic mass of 235U is 235.04, and the atomic mass of 238U is 238.05.)
- If n identical successive separation steps are used, the overall separation is given by the separation in a single step (in this case, the ratio of effusion rates) raised to the nth power. How many effusion steps are needed to obtain 99.0% pure 235UF6?
Given: isotopic content of naturally occurring uranium and atomic masses of 235U and 238U
Asked for: ratio of rates of effusion and number of effusion steps needed to obtain 99.0% pure 235UF6
Strategy:
A Calculate the molar masses of 235UF6 and 238UF6, and then use Graham’s law to determine the ratio of the effusion rates. Use this value to determine the isotopic content of 235UF6 after a single effusion step.
B Divide the final purity by the initial purity to obtain a value for the number of separation steps needed to achieve the desired purity. Use a logarithmic expression to compute the number of separation steps required.
Solution:
- A The first step is to calculate the molar mass of UF6 containing 235U and 238U. Luckily for the success of the separation method, fluorine consists of a single isotope of atomic mass 18.998. The molar mass of 235UF6 is
\[ 234.04 + (6)(18.998) = 349.03 \; g/mol \notag \]
The molar mass of 238UF6 is
\[ 238.05 + (6)(18.998) = 352.04 \; g/mol \notag \]The difference is only 3.01 g/mol (less than 1%). The ratio of the effusion rates can be calculated from Graham’s law using Equation 10.7.10:
\[ \dfrac{rate\; ^{235}UF_{6}}{rate\; ^{238}UF_{6}}=\sqrt{\dfrac{352.04}{349.03}}=1.0043 \notag \]Thus passing UF6 containing a mixture of the two isotopes through a single porous barrier gives an enrichment of 1.0043, so after one step the isotopic content is (0.720%)(1.0043) = 0.723% 235UF6.
- B To obtain 99.0% pure 235UF6 requires many steps. We can set up an equation that relates the initial and final purity to the number of times the separation process is repeated:
\[ final purity = (initial purity)(separation)^{n} \notag \]
In this case, 0.990 = (0.00720)(1.0043)n, which can be rearranged to give
\[ \dfrac{0.990}{0.00720}=1.38=\left ( 1.0043 \right )^{n} \notag \]Taking the logarithm of both sides gives
\[ log\left ( 138 \right )=nlog\left ( 1.0043 \right ) \notag \]
\[ n=\dfrac{log\left ( 138 \right )}{log\left ( 1.0043 \right )} = 1150 = 1.15\times 10^{3} \notag \]
Thus at least a thousand effusion steps are necessary to obtain highly enriched 235U. Figure 10.7.6 shows a small part of a system that is used to prepare enriched uranium on a large scale.
Exercise
Helium consists of two isotopes: 3He (natural abundance = 0.000134%) and 4He (natural abundance = 99.999866%). Their atomic masses are 3.01603 and 4.00260, respectively. Helium-3 has unique physical properties and is used in the study of ultralow temperatures. It is separated from the more abundant 4He by a process of gaseous effusion.
- Calculate the ratio of the effusion rates of 3He and 4He and thus the enrichment possible in a single effusion step.
- How many effusion steps are necessary to yield 99.0% pure 3He?
Answer: a. ratio of effusion rates = 1.15200; one step gives 0.000154% 3He; b. 96 steps
Figure 10.7.6 A Portion of a Plant for Separating Uranium Isotopes by Effusion of UF6
The large cylindrical objects (note the human for scale) are so-called diffuser (actually effuser) units, in which gaseous UF6 is pumped through a porous barrier to partially separate the isotopes. The UF6 must be passed through multiple units to become substantially enriched in 235U.
Rates of Diffusion or Effusion
Graham’s law is an empirical relationship that states that the ratio of the rates of diffusion or effusion of two gases is the square root of the inverse ratio of their molar masses. The relationship is based on the postulate that all gases at the same temperature have the same average kinetic energy. We can write the expression for the average kinetic energy of two gases with different molar masses:
\[ \overline{KE}=\dfrac{1}{2}M_{1}v_{rms_{1}}^{2}=\dfrac{1}{2}M_{2}v_{rms_{2}}^{2} \tag{10.7.11}\]
Multiplying both sides by 2 and rearranging give
\[ \dfrac{v_{rms_{2}}^{2}}{v_{rms_{1}}^{2}}=\dfrac{M_{1}}{M_{2}} \tag{10.7.12}\]
Taking the square root of both sides gives
\[ \dfrac{v_{rms_{2}}}{v_{rms_{1}}}=\sqrt{\dfrac{M_{1}}{M_{2}}} \tag{10.7.13} \]
Thus the rate at which a molecule, or a mole of molecules, diffuses or effuses is directly related to the speed at which it moves. Equation 10.7.13 shows that Graham’s law is a direct consequence of the fact that gaseous molecules at the same temperature have the same average kinetic energy.
Typically, gaseous molecules have a speed of hundreds of meters per second (hundreds of miles per hour). The effect of molar mass on these speeds is dramatic, as illustrated in Figure 10.7.7 for some common gases. Because all gases have the same average kinetic energy, according to the Boltzmann distribution, molecules with lower masses, such as hydrogen and helium, have a wider distribution of speeds. The postulates of the kinetic molecular theory of gases lead to the following equation, which directly relates molar mass, temperature, and rms speed:
\[v_{\rm rms}=\sqrt{\dfrac{3RT}{M}} \tag{10.7.14}\]
In this equation, vrms has units of meters per second; consequently, the units of molar mass M are kilograms per mole, temperature T is expressed in kelvins, and the ideal gas constant R has the value 8.3145 J/(K·mol).
Figure 10.7.7 The Wide Variation in Molecular Speeds Observed at 298 K for Gases with Different Molar Masses
The lightest gases have a wider distribution of speeds and the highest average speeds.
Note the Pattern
Molecules with lower masses have a wider distribution of speeds and a higher average speed.
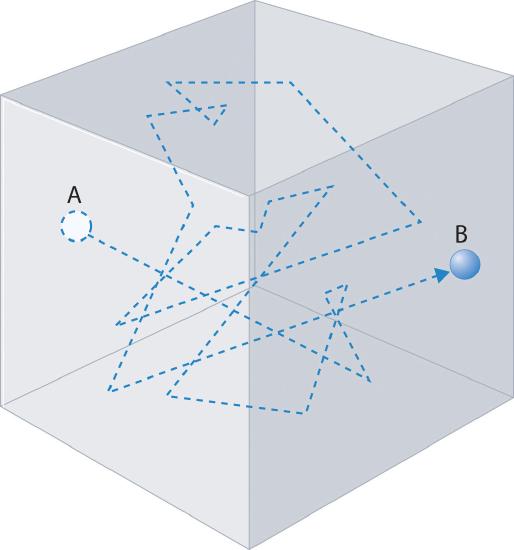
Gas molecules do not diffuse nearly as rapidly as their very high speeds might suggest. If molecules actually moved through a room at hundreds of miles per hour, we would detect odors faster than we hear sound. Instead, it can take several minutes for us to detect an aroma because molecules are traveling in a medium with other gas molecules. Because gas molecules collide as often as 1010 times per second, changing direction and speed with each collision, they do not diffuse across a room in a straight line, as illustrated schematically in Figure 10.7.8 The average distance traveled by a molecule between collisions is the mean free pathThe average distance traveled by a molecule between collisions.. The denser the gas, the shorter the mean free path; conversely, as density decreases, the mean free path becomes longer because collisions occur less frequently. At 1 atm pressure and 25°C, for example, an oxygen or nitrogen molecule in the atmosphere travels only about 6.0 × 10−8 m (60 nm) between collisions. In the upper atmosphere at about 100 km altitude, where gas density is much lower, the mean free path is about 10 cm; in space between galaxies, it can be as long as 1 × 1010 m (about 6 million miles).
Figure 10.7.8 The Path of a Single Particle in a Gas Sample
The frequent changes in direction are the result of collisions with other gas molecules and with the walls of the container.
Note the Pattern
The denser the gas, the shorter the mean free path.
Example 10.7.4
Calculate the rms speed of a sample of cis-2-butene (C4H8) at 20°C.
Given: compound and temperature
Asked for: rms speed
Strategy:
Calculate the molar mass of cis-2-butene. Be certain that all quantities are expressed in the appropriate units and then use Equation 10.39 to calculate the rms speed of the gas.
Solution:
To use Equation 10.7.14, we need to calculate the molar mass of cis-2-butene and make sure that each quantity is expressed in the appropriate units. Butene is C4H8, so its molar mass is 56.11 g/mol. Thus
\[ v_{rms}=\sqrt{\dfrac{3RT}{M}} \tag{10.7.14}\]
Exercise
Calculate the rms speed of a sample of radon gas at 23°C
\[ M = 56.11 \;g/mol = 56.11 \times 10^{-3} \; kg/mol \notag \]
\[ T= 20+273 = 293 \;K \notag \]
\[ R= 8.3145 \; J/\left ( K\cdot mol \right ) = 8.3145 \; \left ( kg\cdot m^{2} \right )/ \left ( s^{2\cdot }K\cdot mol \right ) \notag \]
\[ v_{rms}=\sqrt{\dfrac{3RT}{M}}=\sqrt{\dfrac{3 \cdot 8.3145 \; \left (\cancel{kg}\cdot m^{2} \right )/\left ( s^{2}\cdot \cancel{K \cdot \cancel{mol}} \right )\cdot 293 \; K}{56.11\times 10^{-3} \; \cancel{kg}/\cancel{mol}}} = 3.61\times 10^{2} \; m/s \notag \].
Answer: 1.82 × 102 m/s (about 410 mi/h)
The kinetic molecular theory of gases demonstrates how a successful theory can explain previously observed empirical relationships (laws) in an intuitively satisfying way. Unfortunately, the actual gases that we encounter are not “ideal,” although their behavior usually approximates that of an ideal gas. In Chapter 11 we explore how the behavior of real gases differs from that of ideal gases.
Summary
The behavior of ideal gases is explained by the kinetic molecular theory of gases. Molecular motion, which leads to collisions between molecules and the container walls, explains pressure, and the large intermolecular distances in gases explain their high compressibility. Although all gases have the same average kinetic energy at a given temperature, they do not all possess the same root mean square (rms) speed (vrms). The actual values of speed and kinetic energy are not the same for all particles of a gas but are given by a Boltzmann distribution, in which some molecules have higher or lower speeds (and kinetic energies) than average. Diffusion is the gradual mixing of gases to form a sample of uniform composition even in the absence of mechanical agitation. In contrast, effusion is the escape of a gas from a container through a tiny opening into an evacuated space. The rate of effusion of a gas is inversely proportional to the square root of its molar mass (Graham’s law), a relationship that closely approximates the rate of diffusion. As a result, light gases tend to diffuse and effuse much more rapidly than heavier gases. The mean free path of a molecule is the average distance it travels between collisions.
Key Takeaway
- The kinetic molecular theory of gases provides a molecular explanation for the observations that led to the development of the ideal gas law.
Key Equations
Average kinetic energy
Equation 10.7.6: \[\overline{e_K}=\dfrac{1}{2}m\overline{u^2}=\dfrac{3}{2}\dfrac{R}{N_A}T \]
Root mean square speed
Equation 10.7.8 : \[u_{\rm rms}=\sqrt{\overline{u^2}}=\sqrt{\dfrac{u_1^2+u_2^2+\cdots u_N^2}{N}} \tag{10.7.8}\]
Graham’s law for diffusion and effusion
Equation 10.7.10 \[ \dfrac{r_{1}}{r_{2}}=\dfrac{\sqrt{M_{2}}}{\sqrt{M_{1}}} \tag{10.7.10} \]
Kinetic molecular theory of gases
Equation 10.7.14: \[ v_{rms}=\sqrt{\dfrac{3RT}{M}} \]
Conceptual Problems
-
Which of the following processes represents effusion, and which represents diffusion?
- helium escaping from a hole in a balloon
- vapor escaping from the surface of a liquid
- gas escaping through a membrane
-
Which postulate of the kinetic molecular theory of gases most readily explains the observation that a helium-filled balloon is round?
-
Why is it relatively easy to compress a gas? How does the compressibility of a gas compare with that of a liquid? A solid? Why? Which of the postulates of the kinetic molecular theory of gases most readily explains these observations?
-
What happens to the average kinetic energy of a gas if the rms speed of its particles increases by a factor of 2? How is the rms speed different from the average speed?
-
Which gas—radon or helium—has a higher average kinetic energy at 100°C? Which has a higher average speed? Why? Which postulate of the kinetic molecular theory of gases most readily supports your answer?
-
What is the relationship between the average speed of a gas particle and the temperature of the gas? What happens to the distribution of molecular speeds if the temperature of a gas is increased? Decreased?
-
Qualitatively explain the relationship between the number of collisions of gas particles with the walls of a container and the pressure of a gas. How does increasing the temperature affect the number of collisions?
-
What happens to the average kinetic energy of a gas at constant temperature if the
- volume of the gas is increased?
- pressure of the gas is increased?
-
What happens to the density of a gas at constant temperature if the
- volume of the gas is increased?
- pressure of the gas is increased?
-
Use the kinetic molecular theory of gases to describe how a decrease in volume produces an increase in pressure at constant temperature. Similarly, explain how a decrease in temperature leads to a decrease in volume at constant pressure.
-
Graham’s law is valid only if the two gases are at the same temperature. Why?
-
If we lived in a helium atmosphere rather than in air, would we detect odors more or less rapidly than we do now? Explain your reasoning. Would we detect odors more or less rapidly at sea level or at high altitude? Why?
Numerical Problems
-
At a given temperature, what is the ratio of the rms speed of the atoms of Ar gas to the rms speed of molecules of H2 gas?
-
At a given temperature, what is the ratio of the rms speed of molecules of CO gas to the rms speed of molecules of H2S gas?
-
What is the ratio of the rms speeds of argon and oxygen at any temperature? Which diffuses more rapidly?
-
What is the ratio of the rms speeds of Kr and NO at any temperature? Which diffuses more rapidly?
-
Deuterium (D) and tritium (T) are heavy isotopes of hydrogen. Tritium has an atomic mass of 3.016 amu and has a natural abundance of 0.000138%. The effusion of hydrogen gas (containing a mixture of H2, HD, and HT molecules) through a porous membrane can be used to obtain samples of hydrogen that are enriched in tritium. How many membrane passes are necessary to give a sample of hydrogen gas in which 1% of the hydrogen molecules are HT?
-
Samples of HBr gas and NH3 gas are placed at opposite ends of a 1 m tube. If the two gases are allowed to diffuse through the tube toward one another, at what distance from each end of the tube will the gases meet and form solid NH4Br?
Answer
-
At any temperature, the rms speed of hydrogen is 4.45 times that of argon.
Contributors
- Anonymous
Modified by Joshua Halpern
Figure 10.7.3 by the Backyard Scientist @ YouTube
Figure 10.7.4 frrom NCSSMDistance Ed @ YouTube
Tumbnail from Wikimedia