10.5: Gas Mixtures
- Page ID
- 349461
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To determine the contribution of each component gas to the total pressure of a mixture of gases.
In our use of the ideal gas law thus far, we have focused entirely on the properties of pure gases with only a single chemical species. But what happens when two or more gases are mixed? In this section, we describe how to determine the contribution of each gas present to the total pressure of the mixture.
Partial Pressures
The ideal gas law assumes that all gases behave identically and that their behavior is independent of attractive and repulsive forces. If volume and temperature are held constant, the ideal gas equation can be rearranged to show that the pressure of a sample of gas is directly proportional to the number of moles of gas present:
\[P=n \bigg(\dfrac{RT}{V}\bigg) = n \times \rm const. \tag{10.5.1}\]
Nothing in the equation depends on the nature of the gas—only the amount.
With this assumption, let’s suppose we have a mixture of two ideal gases that are present in equal amounts. What is the total pressure of the mixture? Because the pressure depends on only the total number of particles of gas present, the total pressure of the mixture will simply be twice the pressure of either component. More generally, the total pressure exerted by a mixture of gases at a given temperature and volume is the sum of the pressures exerted by each gas alone. Furthermore, if we know the volume, the temperature, and the number of moles of each gas in a mixture, then we can calculate the pressure exerted by each gas individually, which is its partial pressureThe pressure a gas in a mixture would exert if it were the only one present (at the same temperature and volume)., the pressure the gas would exert if it were the only one present (at the same temperature and volume).
To summarize, the total pressure exerted by a mixture of gases is the sum of the partial pressures of component gases. This law was first discovered by John Dalton, the father of the atomic theory of matter. It is now known as Dalton’s law of partial pressuresA law that states that the total pressure exerted by a mixture of gases is the sum of the partial pressures of component gases.. We can write it mathematically as
\[P_{tot}= P_1+P_2+P_3+P_4 \; ... = \sum_{i=1}^n{P_i} \tag{10.5.2}\]
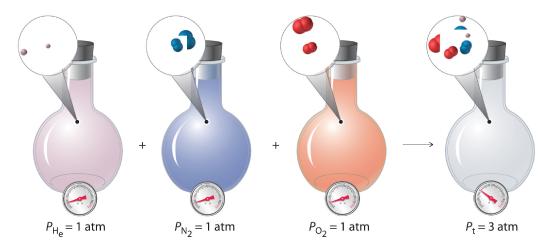
where Pt is the total pressure and the other terms are the partial pressures of the individual gases (Figure 10.5.1).
Figure 10.5.1 Dalton’s Law. The total pressure of a mixture of gases is the sum of the partial pressures of the individual gases.
For a mixture of two ideal gases, A and B, we can write an expression for the total pressure:
\[P_{tot}=P_A+P_B=n_A\bigg(\dfrac{RT}{V}\bigg) + n_B\bigg(\dfrac{RT}{V}\bigg)=(n_A+n_B)\bigg(\dfrac{RT}{V}\bigg) \tag{10.5.3}\]
More generally, for a mixture of i components, the total pressure is given by
\[P_{tot}=(P_1+P_2+P_3+ \; \cdots +P_n)\bigg(\dfrac{RT}{V}\bigg)\tag{10.5.4a}\]
\[P_{tot}=\sum_{i=1}^n{n_i}\bigg(\dfrac{RT}{V}\bigg)\tag{10.5.4b}\]
Equation 10.5.4. restates Equation 10.5.3 in a more general form and makes it explicitly clear that, at constant temperature and volume, the pressure exerted by a gas depends on only the total number of moles of gas present, whether the gas is a single chemical species or a mixture of dozens or even hundreds of gaseous species. For Equation 10.27 to be valid, the identity of the particles present cannot have an effect. Thus an ideal gas must be one whose properties are not affected by either the size of the particles or their intermolecular interactions because both will vary from one gas to another. The calculation of total and partial pressures for mixtures of gases is illustrated in Example 11.
Example 10.5.1
For reasons that we will examine in Chapter 15, deep-sea divers must use special gas mixtures in their tanks, rather than compressed air, to avoid serious problems, most notably a condition called “the bends.” At depths of about 350 ft, divers are subject to a pressure of approximately 10 atm. A typical gas cylinder used for such depths contains 51.2 g of O2 and 326.4 g of He and has a volume of 10.0 L. What is the partial pressure of each gas at 20.00°C, and what is the total pressure in the cylinder at this temperature?
Given: masses of components, total volume, and temperature
Asked for: partial pressures and total pressure
Strategy:
A Calculate the number of moles of He and O2 present.
B Use the ideal gas law to calculate the partial pressure of each gas. Then add together the partial pressures to obtain the total pressure of the gaseous mixture.
Solution:
A The number of moles of He is
\[n_{\rm He}=\rm\dfrac{326.4\;g}{4.003\;g/mol}=81.54\;mol \notag \]
The number of moles of O2 is
\[n_{\rm O_2}=\rm \dfrac{51.2\;g}{32.00\;g/mol}=1.60\;mol \notag \]
B We can now use the ideal gas law to calculate the partial pressure of each:
\[P_{\rm He}=\dfrac{n_{\rm He}RT}{V}=\rm\dfrac{81.54\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=196.2\;atm \notag \]
\[P_{\rm O_2}=\dfrac{n_{\rm O_2}RT}{V}=\rm\dfrac{1.60\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=3.85\;atm \notag \]
The total pressure is the sum of the two partial pressures:
\[P_{\rm tot}=P_{\rm He}+P_{\rm O_2}=\rm(196.2+3.85)\;atm=200.1\;atm \notag \]
Exercise
A cylinder of compressed natural gas has a volume of 20.0 L and contains 1813 g of methane and 336 g of ethane. Calculate the partial pressure of each gas at 22.0°C and the total pressure in the cylinder.
Answer: P(CH4) = 137 atm; P(C2H6) = 13.4 atm; Pt = 151 atm.
Mole Fractions of Gas Mixtures
The composition of a gas mixture can be described by the mole fractions of the gases present. The mole fraction (X)The ratio of the number of moles of any component of a mixture to the total number of moles of all species present in the mixture. of any component of a mixture is the ratio of the number of moles of that component to the total number of moles of all the species present in the mixture (nt):
\[x_A=\dfrac{\text{moles of A}}{\text{total moles}}= \dfrac{n_A}{n_{tot}} =\dfrac{n_A}{n_A+n_B+\cdots}\tag{10.5.6}\]
The mole fraction is a dimensionless quantity between 0 and 1. If XA = 1.0, then the sample is pure A, not a mixture. If XA = 0, then no A is present in the mixture. The sum of the mole fractions of all the components present must equal 1.
To see how mole fractions can help us understand the properties of gas mixtures, let’s evaluate the ratio of the pressure of a gas A to the total pressure of a gas mixture that contains A. We can use the ideal gas law to describe the pressures of both gas A and the mixture: PA = nART/V and Pt = ntRT/V. The ratio of the two is thus
\[\dfrac{P_A}{P_{tot}}=\dfrac{n_ART/V}{n_{tot}RT/V} = \dfrac{n_A}{n_{tot}}=x_A \tag{10.5.7}\]
Rearranging this equation gives
\[P_A = x_AP_{tot} \tag{10.5.8}\]
That is, the partial pressure of any gas in a mixture is the total pressure multiplied by the mole fraction of that gas. This conclusion is a direct result of the ideal gas law, which assumes that all gas particles behave ideally. Consequently, the pressure of a gas in a mixture depends on only the percentage of particles in the mixture that are of that type, not their specific physical or chemical properties. Recall from Chapter 7 (Table 7.6.1) that by volume, Earth’s atmosphere is about 78% N2, 21% O2, and 0.9% Ar, with trace amounts of gases such as CO2, H2O, and others. This means that 78% of the particles present in the atmosphere are N2; hence the mole fraction of N2 is 78%/100% = 0.78. Similarly, the mole fractions of O2 and Ar are 0.21 and 0.009, respectively. Using Equation 10.5.4, we therefore know that the partial pressure of N2 is 0.78 atm (assuming an atmospheric pressure of exactly 760 mmHg) and, similarly, the partial pressures of O2 and Ar are 0.21 and 0.009 atm, respectively.
Example 10.5.2
We have just calculated the partial pressures of the major gases in the air we inhale. Experiments that measure the composition of the air we exhale yield different results, however. The following table gives the measured pressures of the major gases in both inhaled and exhaled air. Calculate the mole fractions of the gases in exhaled air.
| Inhaled Air (mmHg) | Exhaled Air (mmHg) | |
|---|---|---|
| \(P_{\rm N_2}\) | 597 | 568 |
| \(P_{\rm O_2}\) | 158 | 116 |
| \(P_{\rm H_2O}\) | 0.3 | 28 |
| \(P_{\rm CO_2}\) | 5 | 48 |
| P Ar | 8 | 8 |
| P t | 767 | 767 |
Given: pressures of gases in inhaled and exhaled air
Asked for: mole fractions of gases in exhaled air
Strategy:
Calculate the mole fraction of each gas using Equation 10.5.8.
Solution:
The mole fraction of any gas A is given by
\[x_A=\dfrac{P_A}{P_{tot}} \notag \]
where PA is the partial pressure of A and Pt is the total pressure. In this case,
\[x_{\rm CO_2}=\rm\dfrac{48\;mmHg}{767\;mmHg}=0.063 \notag \]
The following table gives the values of PA and XA for exhaled air.
| P A | X A | |
|---|---|---|
| \({\rm N_2}\) | \( \left ( 568 \; \cancel{mmHg} \right )\dfrac{1 \; atm}{760 \; \cancel{mmHg}}= 0.747 \; atm \) | \( \dfrac{0.747 \; \cancel{atm}}{1.01 \; \cancel{atm}} = 0.740 \) |
| \({\rm O_2}\) | \( \left (116 \; \cancel{mmHg} \right )\dfrac{1 \; atm}{760 \; \cancel{mmHg}}= 0.153 \; atm \) | \( \dfrac{0.153 \; \cancel{atm}}{1.01 \; \cancel{atm}} = 0.151 \) |
| \({\rm H_2O}\) | \( \left (28 \; \cancel{mmHg} \right )\dfrac{1 \; atm}{760 \; \cancel{mmHg}}= 0.037 \; atm \) | \( \dfrac{0.031 \; \cancel{atm}}{1.01 \; \cancel{atm}} = 0.031 \) |
| \({\rm CO_2}\) | \( \left (48 \; \cancel{mmHg} \right )\dfrac{1 \; atm}{760 \; \cancel{mmHg}}= 0.063 \; atm \) | \( \dfrac{0.063 \; \cancel{atm}}{1.01 \; \cancel{atm}} = 0.061 \) |
| \({\rm Ar}\) | \( \left (8 \; \cancel{mmHg} \right )\dfrac{1 \; atm}{760 \; \cancel{mmHg}}= 0.011 \; atm \) | \( \dfrac{0.011 \; \cancel{atm}}{1.01 \; \cancel{atm}} = 0.011 \) |
Exercise
We saw in Example 10 that Venus is an inhospitable place, with a surface temperature of 560°C and a surface pressure of 90 atm. The atmosphere consists of about 96% CO2 and 3% N2, with trace amounts of other gases, including water, sulfur dioxide, and sulfuric acid. Calculate the partial pressures of CO2 and N2.
Answer: \(P_{\rm CO_2}=\rm86\; atm\), \(P_{\rm N_2}=\rm2.7\;atm\)
Summary
The pressure exerted by each gas in a gas mixture (its partial pressure) is independent of the pressure exerted by all other gases present. Consequently, the total pressure exerted by a mixture of gases is the sum of the partial pressures of the components (Dalton’s law of partial pressures). The amount of gas present in a mixture may be described by its partial pressure or its mole fraction. The mole fraction of any component of a mixture is the ratio of the number of moles of that substance to the total number of moles of all substances present. In a mixture of gases, the partial pressure of each gas is the product of the total pressure and the mole fraction of that gas.
Key Takeaway
- The partial pressure of each gas in a mixture is proportional to its mole fraction.
Key Equations
Mole fraction
Equation 10.5.7: \( X_{A}= \dfrac{moles A}{total moles} = \dfrac{n_{A}}{n_{t}} \)
Relationship between partial pressure and mole fraction
Equation 10.5.8: PA = XAPt
Conceptual Problems
-
Dalton’s law of partial pressures makes one key assumption about the nature of the intermolecular interactions in a mixture of gases. What is it?
-
What is the relationship between the partial pressure of a gas and its mole fraction in a mixture?
Numerical Problems
-
What is the partial pressure of each gas if the following amounts of substances are placed in a 25.0 L container at 25°C? What is the total pressure of each mixture?
- 1.570 mol of CH4 and 0.870 mol of CO2
- 2.63 g of CO and 1.24 g of NO2
- 1.78 kg of CH3Cl and 0.92 kg of SO2
-
What is the partial pressure of each gas in the following 3.0 L mixtures at 37°C as well as the total pressure?
- 0.128 mol of SO2 and 0.098 mol of methane (CH4)
- 3.40 g of acetylene (C2H2) and 1.54 g of He
- 0.267 g of NO, 4.3 g of Ar, and 0.872 g of SO2
-
In a mixture of helium, oxygen, and methane in a 2.00 L container, the partial pressures of He and O2 are 13.6 kPa and 29.2 kPa, respectively, and the total pressure inside the container is 95.4 kPa. What is the partial pressure of methane? If the methane is ignited to initiate its combustion with oxygen and the system is then cooled to the original temperature of 30°C, what is the final pressure inside the container (in kilopascals)?
-
A 2.00 L flask originally contains 1.00 g of ethane (C2H6) and 32.0 g of oxygen at 21°C. During ignition, the ethane reacts completely with oxygen to produce CO2 and water vapor, and the temperature of the flask increases to 200°C. Determine the total pressure and the partial pressure of each gas before and after the reaction.
-
If a 20.0 L cylinder at 19°C is charged with 5.0 g each of sulfur dioxide and oxygen, what is the partial pressure of each gas? The sulfur dioxide is ignited in the oxygen to produce sulfur trioxide gas, and the mixture is allowed to cool to 19°C at constant pressure. What is the final volume of the cylinder? What is the partial pressure of each gas in the piston?
-
The highest point on the continent of Europe is Mt. Elbrus in Russia, with an elevation of 18,476 ft. The highest point on the continent of South America is Mt. Aconcagua in Argentina, with an elevation of 22,841 ft.
- The following table shows the variation of atmospheric pressure with elevation. Use the data in the table to construct a plot of pressure versus elevation.
Elevation (km) Pressure in Summer (mmHg) Pressure in Winter (mmHg) 0.0 760.0 760.0 1.0 674.8 670.6 1.5 635.4 629.6 2.0 598.0 590.8 3.0 528.9 519.7 5.0 410.6 398.7 7.0 314.9 301.6 9.0 237.8 224.1 - Use your graph to estimate the pressures in millimeters of mercury during the summer and the winter at the top of both mountains in both atmospheres and kilopascals.
- Given that air is 20.95% O2 by volume, what is the partial pressure of oxygen in atmospheres during the summer at each location?
- The following table shows the variation of atmospheric pressure with elevation. Use the data in the table to construct a plot of pressure versus elevation.
Answers
-
- P(CH4) = 1.54 atm, P(CO2) = 0.851 atm, PT = 2.39 atm
- P(CO) = 0.0918 atm, P(NO2) = 0.0264 atm, PT = 0.1182 atm
- P( CH3Cl) = 34.5 atm, P(SO2) = 14 atm, PT = 49 atm
-
52.6 kPa, 66.2 kPa