13.4: The Law of Chemical Equilibrium
- Page ID
- 49518
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Two examples of an equilibrium constant dealt with in other sections, namely:
\[K_{c}=\frac{[trans\text{-C}_{\text{2}}\text{H}_{\text{2}}\text{F}_{\text{2}}]}{[cis\text{-C}_{\text{2}}\text{H}_{\text{2}}\text{F}_{\text{2}}]} \nonumber \]
for the reaction
\[\text{cis-C}_2\text{H}_2\text{F}_2 \rightleftharpoons \text{trans-C}_2\text{H}_2\text{F}_2 \nonumber \]
In the equation above, notice that both sides have the same molecular formula, yet in the image below, the elements involved are arranged differently. These molecules are called isomers and to learn more about them, check out the following site: https://www.thoughtco.com/geometric-isomerism-cis-and-trans-608702.
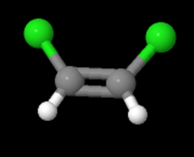
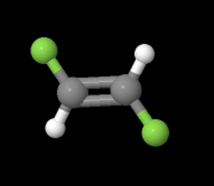
and
\[K_{c}=\frac{[\text{ NO}_{\text{2}}]^{\text{2}}}{[\text{ N}_{\text{2}}\text{O}_{\text{4}}]} \nonumber \]
for the reaction
\[\text{N}_2\text{O}_4 \rightleftharpoons \text{2NO}_2 \nonumber \]
In the equation above, we see the decomposition of N2O4 (the clear gas pictured below) into NO2, which is the brownish red gas seen below. As you can see in the molecular structure above, this decomposition of N2O4 occurs when the middle bond holding N2O4 together is broken, leaving two NO2 molecules. For more information on this specific equilibrium, check out the page on The Effect of a Change in Temperature.
Both the trans-cis transition of C2H2F2 and the decomposition of N2O4 are particular examples of a more general law governing chemical equilibrium in gases. If we write an equation for a gaseous equilibrium in general in the form
\[aA(g) + bB(g) \rightleftharpoons cC(g) + dD(g) \label{1} \]
then the equilibrium constant defined by the equation
\[K_{c}=\frac{[\text{ C }]^{c}[\text{ D }]^{d}}{[\text{ A }]^{a}[\text{ B }]^{b}} \label{2} \]
is found to be a constant quantity depending only on the temperature and the nature of the reaction. This general result is called the law of chemical equilibrium, or the law of mass action.
Write expressions for the equilibrium constant for the following reactions:
- \[\text{2HI}(g) \rightleftharpoons \text{H}_2(g) + \text{I}_2(g) \nonumber \]
- \[\text{N}_2(g) + \text{3H}_2(g) \rightleftharpoons \text{2NH}_3(g) \nonumber \]
- \[\text{O}_2(g) + \text{4HCl}(g) \rightleftharpoons \text{2H}_2\text{O}(g) + \text{2Cl}_2(g) \nonumber \]
Solution
- \[K_{c}=\frac{[\text{ H}_{\text{2}}]\text{ }[\text{ I}_{\text{2}}]}{[\text{ HI }]^{\text{2}}} \nonumber \]
- \[K_{c}=\frac{[\text{ NH}_{\text{3}}]^{\text{2}}}{[\text{ N}_{\text{2}}]\text{ }[\text{ H}_{\text{2}}]^{3}} \nonumber \]
- \[K_{c}=\frac{[\text{ H}_{\text{2}}\text{O }]^{\text{2}}[\text{ Cl}_{\text{2}}]^{\text{2}}}{[\text{ O}_{\text{2}}]\text{ }[\text{ HCl }]^{\text{4}}} \nonumber \]
A mixture containing equal concentrations of methane and steam is passed over a nickel catalyst at 1000 K. The emerging gas has the composition [CO] = 0.1027 mol dm–3, [H2] = 0.3080 mol dm–3, and [CH4] = [H2O] = 0.8973 mol dm–3. Assuming this mixture is at equilibrium, calculate the equilibrium constant Kc for the reaction
\[\text{CH}_4(g) + \text{H}_2\text{O}(g) \rightleftharpoons \text{CO}(g) + \text{3H}_2(g) \nonumber \]
Solution
The equilibrium constant is given by the following equation:
\[K_{c}=\frac{[\text{ CO }]\text{ }[\text{ H}_{\text{2}}]^{\text{3}}}{[\text{ CH}_{\text{4}}]\text{ }[\text{ H}_{\text{2}}\text{O }]}=\frac{\text{0}\text{.1027}^{-\text{3}}\times \text{ (0}\text{.3080}^{-\text{3}}\text{)}^{\text{3}}}{\text{0}\text{.8973}^{-\text{3}}\times \text{ 0}\text{.8973}^{-\text{3}}} \nonumber \]
\[=\text{3}\text{.727 }\times \text{ 10}^{-\text{3}} \nonumber \]
Note: The yield of H2 at this temperature is quite poor. In the commercial production of H2 from natural gas, the reaction is run at a somewhat higher temperature where the value Kc is larger.
As the above example shows, the equilibrium constant Kc is a dimensionless quantity. This lack of units is a result of the derivation of Kc from Keq which uses the activities of the reactants and products in the equilibrium system instead of their concentrations. The activity of a substance is a measure of its effective concentration under specified conditions. While a detailed discussion of this important quantity is beyond the scope of an introductory text, it is necessary to be aware of a few important aspects:
- Activities are dimensionless (unitless) quantities and are in essence “adjusted” concentrations.
- For relatively dilute solutions, a substance's activity and its molar concentration are roughly equal. However, to obtain a unitless quantity, each molar concentration is divided by a standard state defined as 1 \(\dfrac{mole}{dm^{3}}\). By using this standard state, the numerical value of the concentration remains unchanged, but the units cancel out.
- Activities for pure condensed phases (solids and liquids) are equal to 1.
- Activities for solvents in dilute solutions are equal to 1.
Thus, when we apply the equilibrium law to reactions which involve pure solids and pure liquids, we find in such cases that as long as some solid or liquid is present, the actual amount does not affect the position of equilibrium. Accordingly, only the molar concentrations of gaseous species are explicitly written in the expression for the equilibrium constant. For example, the equilibrium constant for the reaction
\[\text{CaCO}_3(s) \rightleftharpoons \text{CaO}(s) + \text{CO}_2(g) \label{3} \]
Notice below the molecular representation of the above reaction, with the ionic structure of CaCO3 'breaking apart' to form the simpler ionic structure CaO as well as gaseous CO2.
is given by the expression
\[\text{K}_c = [\text{CO}_2] \label{4} \]
in which only the concentration of the gas appears explicitly because the two solids each have an activity with a value equal to 1. Equation \(\ref{4}\) suggests that if we heat CaCO3 to a high temperature so that some of it decomposes, the concentration of CO2 at equilibrium will depend only on the temperature and will not change if the ratio of amount of solid CaCO3 to amount of solid CaO is altered. Experimentally this is what is observed.
Write expressions for the equilibrium constants for the following reactions:
- \[\text{C}(s) + \text{H}_2\text{O}(g) \rightleftharpoons \text{CO}(g) + \text{H}_2(g) \nonumber \]
- \[\text{C}(s) + \text{CO}_2(g) \rightleftharpoons \text{2CO}(g) \nonumber \]
- \[\text{Fe}_3\text{O}_4(s) + \text{H}_2(g) \rightleftharpoons \text{3FeO}(s) + \text{H}_2\text{O}(g) \nonumber \]
Solution
Since only gaseous species need be included, we obtain
- \[K_{c}=\frac{[\text{ CO }]\text{ }[\text{ H}_{\text{2}}]}{[\text{ H}_{\text{2}}\text{O }]} \nonumber \]
- \[K_{c}=\frac{[\text{ CO }]^{\text{2}}}{[\text{ CO}_{\text{2}}]} \nonumber \]
- \[K_{c}=\frac{[\text{ H}_{\text{2}}\text{O }]}{[\text{ H}_{\text{2}}]} \nonumber \]
The equilibrium law can be shown experimentally to apply to dilute liquid solutions as well as to mixtures of gases, and the equilibrium-constant expression for a solution reaction can be obtained in the same way as for a gas-phase reaction.
Acetic acid, for example, reacts as follows when it dissolves in water:
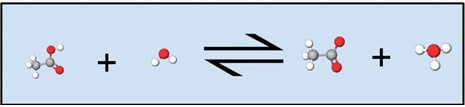
\[\text{CH}_3\text{COOH}(aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{CH}_3\text{COO}^{-}(aq) + \text{H}_3\text{O}^{+} (aq)\label{5} \]
Notice in the figure below how the white hydrogen attached to the red oxygen on the acetic acid molecule is transferred to water, forming acetate (acetic acid minus a hydrogen) and a hydronium ion. Symbolically in the equation above, we can see this same transfer, except hydrogen is represented as an H rather than a white ball.
In solution only the concentrations of the solute species are explicitly shown in the equilibrium law. Even though the solvent may be a reactant or product, as long as the solution is dilute, any small amount of water produced or used by the chemical reaction will not change the amount of water to an appreciable extent because it is the solvent. As the solvent, water is assigned an activity equal to 1. Thus the activity of water is conventionally not explicitly written as part of the equilibrium law for a reaction in aqueous solution. Since it applies to a weak acid, Ka is called an acid constant. (The a stands for acid.) Other equilibrium constants in which the activity of the solvent water has a value of 1 and is thus not explicitly included in the equilibrium law are the base constant, Kb, for ionization of a weak base and the solubility product constant, Ksp, for dissolution of a slightly soluble compound.
The activity of the solvent in a dilute solution has a defined value of 1. This activity is part of the equilibrium law, but it is conventionally not written in the equilibrium law because its numerical value of 1 does not change the numerical value of the equilibrium constant.
It is a common error to claim that the molar concentration of the solvent is in someway involved in the equilibrium law. This error is a result of a misunderstanding of solution thermodynamics. For example, it is often claimed that Kc = Keq[H2O] for aqueous solutions. This equation is incorrect because it is an erroneous interpretation of the correct equation Kc = Keq(\(\textit{a}_{H_2O}\)). Because \(\textit{a}_{H_2O}\) = 1 for a dilute solution, Ka = Keq(1), or Ka = Keq.
Write out expressions for the equilibrium constants for the following ionic equilibria in dilute aqueous solution:
- \[\text{HF}(aq) + \text{H}_2\text{O} \rightleftharpoons \text{F}^{-}(aq) + \text{H}_3\text{O}^{+}(aq) \nonumber \]
- \[\text{H}_2\text{O} + \text{NH}_3(aq) \rightleftharpoons \text{OH}^{-}(aq) + \text{NH}_4^{+}(aq) \nonumber \]
- \[\text{H}_2\text{O} + \text{CO}_3^{2-}(aq) \rightleftharpoons \text{HCO}_3^{-}(aq) + \text{OH}^{-}(aq) \nonumber \]
- \[\text{BaSO}_4(s) \rightleftharpoons \text{Ba}^{2+}(aq) + \text{SO}_4^{2-}(aq) \nonumber \]
Solution
We do not explicitly include the activity of H2O in the first three examples and the activity of solid BaSO4 in the fourth because in all of these cases, the acivity of the specific species is equal to 1, and thus would not change the numerical value of the equilibrium constant..
- \[\text{K}_a = \text{K}_c = \frac{[\text{ H}_{\text{3}}\text{O}^{\text{+}}]\text{ }[\text{ F}^{-}]}{[\text{ HF }]} \nonumber \]
- \[\text{K}_b = \text{K}_c = \frac{[\text{ NH}_{\text{4}}^{\text{+}}]\text{ }[\text{ OH}^{-}]}{[\text{ NH}_{\text{3}}]} \nonumber \]
- \[\text{K}_b =\text{K}_c = \frac{[\text{ HCO}_{\text{3}}^{-}]\text{ }[\text{ OH}^{-}]}{[\text{ CO}_{\text{3}}^{\text{2}-}]} \nonumber \]
- \[\text{K}_{sp} = \text{K}_c = [\text{Ba}^{2+}][\text{SO}_4^{2-}] \nonumber \]
Measurements of the conductivities of acetic acid solutions indicate that the fraction of acetic acid molecules converted to acetate and hydronium ions is
- 0.0296 at a concentration of 0.020 00 mol dm–3
- 0.5385 at a concentration of 2.801 × 10–5 mol dm–3
Use these data to calculate the equilibrium constant for Equation (5) at each concentration.
Solution
Consider first 1 dm3 of solution a. This originally contained 0.02 mol CH3COOH of which the fraction 0.0296 has ionized. Thus (1 – 0.0296) × 0.02 mol undissociated CH3COOH is left, while 0.0296 × 0.02 mol H3O+ and CH3COO– have been produced. In tabular form
| Substance | Original Amount | Amount Produced | Equilibrium Amount | Equilibrium Concentration |
| CH3COOH | 0.02 mol | -0.0296×0.02 mol | (0.02-0.000 592) mol | 0.0194 mol dm-3 |
| H3+ | 0 mol | +0.0296×0.02mol | 0.000 592 mol | 5.92×10-4 mol dm-3 |
| CH3COO- | 0 mol | +0.0296×0.02 mol | 0.000 592 mol | 5.92×10-4 mol dm-3 |
Substituting into the expression for Ka gives
\[K_{a}=\frac{[\text{ CH}_{\text{3}}\text{COO}^{-}]\text{ }[\text{ H}_{\text{3}}\text{O}^{\text{+}}]}{[\text{ CH}_{\text{3}}\text{COOH }]}=\frac{\text{(5}\text{.92 }\times \text{ 10}^{-\text{4}}\text{)}^{\text{2}}}{\text{0}\text{.0194}}=\text{1}\text{.81 }\times \text{ 10}^{-\text{5}} \nonumber \]
A similar calculation on the second solution yields
\[K_{a}=\frac{\text{(1}\text{.5083 }\times \text{ 10}^{-\text{5}}\text{)}^{\text{2}}}{\text{1}\text{.2926 }\times \text{ 10}^{-\text{5}}}=\text{1}\text{.760 }\times \text{ 10}^{-\text{5}} \nonumber \]
The two values of the equilibrium constant are only in approximate agreement. In more concentrated solutions the agreement is worse. If the concentration is 1 mol dm–3, for instance, Ka has the value 1.41 × 10–5. This is the reason for our statement that the equilibrium law applies to dilute solutions.
Acknowledgements
molview.org was used to create the molecular representations found on this webpage. Check out the site at the following link: Molview.


