9.8: Molecular Orbital Theory
- Page ID
- 3513
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential ideas
- In what fundamental way does the molecular orbital model differ from the other models of chemical bonding that have been described in these lessons?
- Explain how bonding and antibonding orbitals arise from atomic orbitals, and how they differ physically.
- Describe the essential difference between a sigma and a pi molecular orbital.
- Define bond order, and state its significance.
- Construct a "molecular orbital diagram" of the kind shown in this lesson for a simple diatomic molecule, and indicate whether the molecule or its positive and negative ions should be stable.
The molecular orbital model is by far the most productive of the various models of chemical bonding, and serves as the basis for most quantiative calculations, including those that lead to many of the computer-generated images that you have seen elsewhere in these units. In its full development, molecular orbital theory involves a lot of complicated mathematics, but the fundamental ideas behind it are quite easily understood, and this is all we will try to accomplish in this lesson.
This is a big departure from the simple Lewis and VSEPR models that were based on the one-center orbitals of individual atoms. The more sophisticated hybridization model recognized that these orbitals will be modified by their interaction with other atoms. But all of these valence-bond models, as they are generally called, are very limited in their applicability and predictive power, because they fail to recognize that distribution of the pooled valence electrons is governed by the totality of positive centers.
Molecular Orbitals
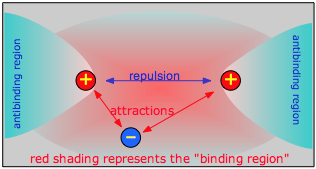
Chemical bonding occurs when the net attractive forces between an electron and two nuclei exceeds the electrostatic repulsion between the two nuclei. For this to happen, the electron must be in a region of space which we call the binding region. Conversely, if the electron is off to one side, in an anti-binding region, it actually adds to the repulsion between the two nuclei and helps push them away.
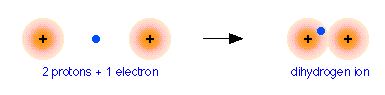
The easiest way of visualizing a molecular orbital is to start by picturing two isolated atoms and the electron orbitals that each would have separately. These are just the orbitals of the separate atoms, by themselves, which we already understand. We will then try to predict the manner in which these atomic orbitals interact as we gradually move the two atoms closer together. Finally, we will reach some point where the internuclear distance corresponds to that of the molecule we are studying. The corresponding orbitals will then be the molecular orbitals of our new molecule.
To see how this works, we will consider the simplest possible molecule, \(\ce{H2^{+}}\). This is the hydrogen molecule ion, which consists of two nuclei of charge +1, and a single electron shared between them.
As two H nuclei move toward each other, the 1s atomic orbitals of the isolated atoms gradually merge into a new molecular orbital in which the greatest electron density falls between the two nuclei. Since this is just the location in which electrons can exert the most attractive force on the two nuclei simultaneously, this arrangement constitutes a bonding molecular orbital. Regarding it as a three- dimensional region of space, we see that it is symmetrical about the line of centers between the nuclei; in accord with our usual nomenclature, we refer to this as a σ (sigma) orbital.
Bonding and Antibonding Molecular Orbitals
There is one minor difficulty: we started with two orbitals (the 1s atomic orbitals), and ended up with only one orbital. Now according to the rules of quantum mechanics, orbitals cannot simply appear and disappear at our convenience. For one thing, this would raise the question of at just what internuclear distance do we suddenly change from having two orbitals, to having only one? It turns out that when orbitals interact, they are free to change their forms, but there must always be the same number. This is just another way of saying that there must always be the same number of possible allowed sets of electron quantum numbers.
How can we find the missing orbital? To answer this question, we must go back to the wave-like character of orbitals that we developed in our earlier treatment of the hydrogen atom. You are probably aware that wave phenomena such as sound waves, light waves, or even ocean waves can combine or interact with one another in two ways: they can either reinforce each other, resulting in a stronger wave, or they can interfere with and partially destroy each other. A roughly similar thing occurs when the “matter waves” corresponding to the two separate hydrogen 1s orbitals interact; both in-phase and out-of-phase combinations are possible, and both occur. The in-phase, reinforcing interaction yields the bonding orbital that we just considered. The other, corresponding to out-of-phase combination of the two orbitals, gives rise to a molecular orbital that has its greatest electron probability in what is clearly the antibonding region of space. This second orbital is therefore called an antibonding orbital.
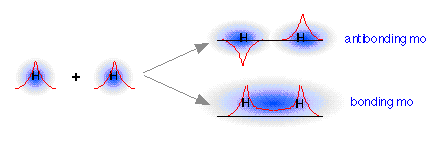
When the two 1s wave functions combine out-of-phase, the regions of high electron probability do not merge. In fact, the orbitals act as if they actually repel each other. Notice particularly that there is a region of space exactly equidistant between the nuclei at which the probability of finding the electron is zero. This region is called a nodal surface, and is characteristic of antibonding orbitals. It should be clear that any electrons that find themselves in an antibonding orbital cannot possibly contribute to bond formation; in fact, they will actively oppose it.
We see, then, that whenever two orbitals, originally on separate atoms, begin to interact as we push the two nuclei toward each other, these two atomic orbitals will gradually merge into a pair of molecular orbitals, one of which will have bonding character, while the other will be antibonding. In a more advanced treatment, it would be fairly easy to show that this result follows quite naturally from the wave-like nature of the combining orbitals.
What is the difference between these two kinds of orbitals, as far as their potential energies are concerned? More precisely, which kind of orbital would enable an electron to be at a lower potential energy? Clearly, the potential energy decreases as the electron moves into a region that enables it to “see” the maximum amount of positive charge. In a simple diatomic molecule, this will be in the internuclear region— where the electron can be simultaneously close to two nuclei. The bonding orbital will therefore have the lower potential energy.
Molecular Orbital Diagrams
This scheme of bonding and antibonding orbitals is usually depicted by a molecular orbital diagram such as the one shown here for the dihydrogen ion H2+. Atomic valence electrons (shown in boxes on the left and right) fill the lower-energy molecular orbitals before the higher ones, just as is the case for atomic orbitals. Thus, the single electron in this simplest of all molecules goes into the bonding orbital, leaving the antibonding orbital empty.
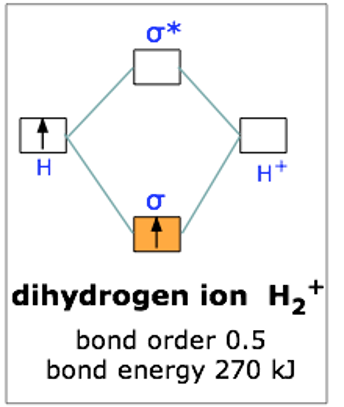
Since any orbital can hold a maximum of two electrons, the bonding orbital in H2+is only half-full. This single electron is nevertheless enough to lower the potential energy of one mole of hydrogen nuclei pairs by 270 kJ— quite enough to make them stick together and behave like a distinct molecular species. Although H2+ is stable in this energetic sense, it happens to be an extremely reactive molecule— so much so that it even reacts with itself, so these ions are not commonly encountered in everyday chemistry.
Dihydrogen
If one electron in the bonding orbital is conducive to bond formation, might two electrons be even better? We can arrange this by combining two hydrogen atoms-- two nuclei, and two electrons. Both electrons will enter the bonding orbital, as depicted in the Figure.
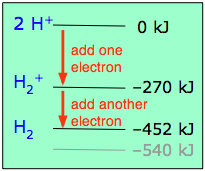
We recall that one electron lowered the potential energy of the two nuclei by 270 kJ/mole, so we might expect two electrons to produce twice this much stabilization, or 540 kJ/mole.
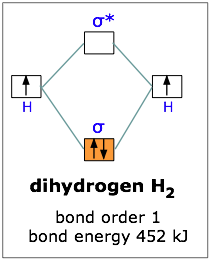
Experimentally, one finds that it takes only 452 kJ to break apart a mole of hydrogen molecules. The reason the potential energy was not lowered by the full amount is that the presence of two electrons in the same orbital gives rise to a repulsion that acts against the stabilization. This is exactly the same effect we saw in comparing the ionization energies of the hydrogen and helium atoms.
Dihelium
With two electrons we are still ahead, so let’s try for three. The dihelium positive ion is a three-electron molecule. We can think of it as containing two helium nuclei and three electrons. This molecule is stable, but not as stable as dihydrogen; the energy required to break He2+ is 301 kJ/mole. The reason for this should be obvious; two electrons were accommodated in the bonding orbital, but the third electron must go into the next higher slot— which turns out to be the sigma antibonding orbital. The presence of an electron in this orbital, as we have seen, gives rise to a repulsive component which acts against, and partially cancels out, the attractive effect of the filled bonding orbital.
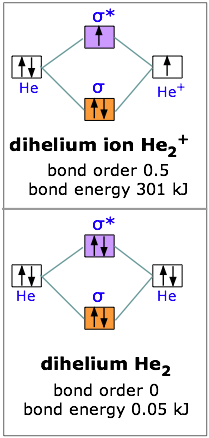
Taking our building-up process one step further, we can look at the possibilities of combining to helium atoms to form dihelium. You should now be able to predict that He2 cannot be a stable molecule; the reason, of course, is that we now have four electrons— two in the bonding orbital, and two in the antibonding orbital. The one orbital almost exactly cancels out the effect of the other. Experimentally, the bond energy of dihelium is only .084 kJ/mol; this is not enough to hold the two atoms together in the presence of random thermal motion at ordinary temperatures, so dihelium dissociates as quickly as it is formed, and is therefore not a distinct chemical species.
Diatomic molecules containing second-row atoms
The four simplest molecules we have examined so far involve molecular orbitals that derived from two 1s atomic orbitals. If we wish to extend our model to larger atoms, we will have to contend with higher atomic orbitals as well. One greatly simplifying principle here is that only the valence-shell orbitals need to be considered. Inner atomic orbitals such as 1s are deep within the atom and well-shielded from the electric field of a neighboring nucleus, so that these orbitals largely retain their atomic character when bonds are formed.
Dilithium
For example, when lithium, whose configuration is 1s22s1, bonds with itself to form Li2, we can forget about the 1s atomic orbitals and consider only the σ bonding and antibonding orbitals. Since there are not enough electrons to populate the antibonding orbital, the attractive forces win out and we have a stable molecule.
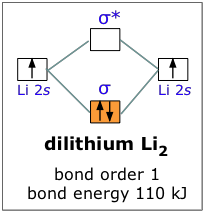
The bond energy of dilithium is 110 kJ/mole; notice that this value is less than half of the 270 kJ bond energy in dihydrogen, which also has two electrons in a bonding orbital. The reason, of course, is that the 2s orbital of Li is much farther from its nucleus than is the 1s orbital of H, and this is equally true for the corresponding molecular orbitals. It is a general rule, then, that the larger the parent atom, the less stable will be the corresponding diatomic molecule.
Lithium hydride
All the molecules we have considered thus far are homonuclear; they are made up of one kind of atom. As an example of a heteronuclear molecule, let’s take a look at a very simple example— lithium hydride. Lithium hydride is a stable, though highly reactive molecule. The diagram shows how the molecular orbitals in lithium hydride can be related to the atomic orbitals of the parent atoms. One thing that makes this diagram look different from the ones we have seen previously is that the parent atomic orbitals have widely differing energies; the greater nuclear charge of lithium reduces the energy of its 1s orbital to a value well below that of the 1s hydrogen orbital.
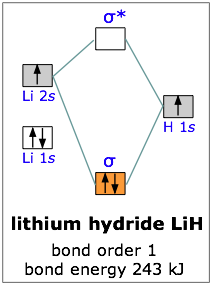
There are two occupied atomic orbitals on the lithium atom, and only one on the hydrogen. With which of the lithium orbitals does the hydrogen 1s orbital interact? The lithium 1s orbital is the lowest-energy orbital on the diagram. Because this orbital is so small and retains its electrons so tightly, it does not contribute to bonding; we need consider only the 2s orbital of lithium which combines with the 1s orbital of hydrogen to form the usual pair of sigma bonding and antibonding orbitals. Of the four electrons in lithium and hydrogen, two are retained in the lithium 1s orbital, and the two remaining ones reside in the σ orbital that constitutes the Li–H covalent bond.
The resulting molecule is 243 kJ/mole more stable than the parent atoms. As we might expect, the bond energy of the heteronuclear molecule is very close to the average of the energies of the corresponding homonuclear molecules. Actually, it turns out that the correct way to make this comparison is to take the geometric mean, rather than the arithmetic mean, of the two bond energies. The geometric mean is simply the square root of the product of the two energies.
The geometric mean of the H2 and Li2 bond energies is 213 kJ/mole, so it appears that the lithium hydride molecule is 30 kJ/mole more stable than it “is supposed” to be. This is attributed to the fact that the electrons in the 2σ bonding orbital are not equally shared between the two nuclei; the orbital is skewed slightly so that the electrons are attracted somewhat more to the hydrogen atom. This bond polarity, which we considered in some detail near the beginning of our study of covalent bonding, arises from the greater electron-attracting power of hydrogen— a consequence of the very small size of this atom. The electrons can be at a lower potential energy if they are slightly closer to the hydrogen end of the lithium hydride molecule. It is worth pointing out, however, that the electrons are, on the average, also closer to the lithium nucleus, compared to where they would be in the 2s orbital of the isolated lithium atom. So it appears that everyone gains and no one loses here!
\(\Sigma\) and \(\pi\) orbitals
The molecules we have considered thus far are composed of atoms that have no more than four electrons each; our molecular orbitals have therefore been derived from s-type atomic orbitals only. If we wish to apply our model to molecules involving larger atoms, we must take a close look at the way in which p-type orbitals interact as well. Although two atomic p orbitals will be expected to split into bonding and antibonding orbitals just as before, it turns out that the extent of this splitting, and thus the relative energies of the resulting molecular orbitals, depend very much on the nature of the particular p orbital that is involved.
You will recall that there are three possible p orbitals for any value of the principal quantum number. You should also recall that p orbitals are not spherical like s orbitals, but are elongated, and thus possess definite directional properties. The three p orbitals correspond to the three directions of Cartesian space, and are frequently designated px, py, and pz, to indicate the axis along which the orbital is aligned. Of course, in the free atom, where no coordinate system is defined, all directions are equivalent, and so are the p orbitals. But when the atom is near another atom, the electric field due to that other atom acts as a point of reference that defines a set of directions. The line of centers between the two nuclei is conventionally taken as the x axis. If this direction is represented horizontally on a sheet of paper, then the y axis is in the vertical direction and the z axis would be normal to the page.

These directional differences lead to the formation of two different classes of molecular orbitals. The above figure shows how two px atomic orbitals interact. In many ways the resulting molecular orbitals are similar to what we got when s atomic orbitals combined; the bonding orbital has a large electron density in the region between the two nuclei, and thus corresponds to the lower potential energy. In the out-of-phase combination, most of the electron density is away from the internuclear region, and as before, there is a surface exactly halfway between the nuclei that corresponds to zero electron density. This is clearly an antibonding orbital— again, in general shape, very much like the kind we saw in hydrogen and similar molecules. Like the ones derived from s-atomic orbitals, these molecular orbitals are σ (sigma) orbitals.
Sigma orbitals are cylindrically symmetric with respect to the line of centers of the nuclei; this means that if you could look down this line of centers, the electron density would be the same in all directions.
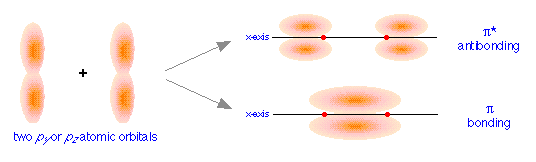
orbitals, we get the bonding and antibonding pairs that we would expect, but the resulting molecular orbitals have a different symmetry: rather than being rotationally symmetric about the line of centers, these orbitals extend in both perpendicular directions from this line of centers. Orbitals having this more complicated symmetry are called π (pi) orbitals. There are two of them, πy and πz differing only in orientation, but otherwise completely equivalent.
The different geometric properties of the π and σ orbitals causes the latter orbitals to split more than the π orbitals, so that the σ* antibonding orbital always has the highest energy. The σ bonding orbital can be either higher or lower than the π bonding orbitals, depending on the particular atom.
Second-Row Diatomics
If we combine the splitting schemes for the 2s and 2p orbitals, we can predict bond order in all of the diatomic molecules and ions composed of elements in the first complete row of the periodic table. Remember that only the valence orbitals of the atoms need be considered; as we saw in the cases of lithium hydride and dilithium, the inner orbitals remain tightly bound and retain their localized atomic character.
Dicarbon
Carbon has four outer-shell electrons, two 2s and two 2p. For two carbon atoms, we therefore have a total of eight electrons, which can be accommodated in the first four molecular orbitals. The lowest two are the 2s-derived bonding and antibonding pair, so the “first” four electrons make no net contribution to bonding. The other four electrons go into the pair of pibonding orbitals, and there are no more electrons for the antibonding orbitals— so we would expect the dicarbon molecule to be stable, and it is. (But being extremely reactive, it is known only in the gas phase.)
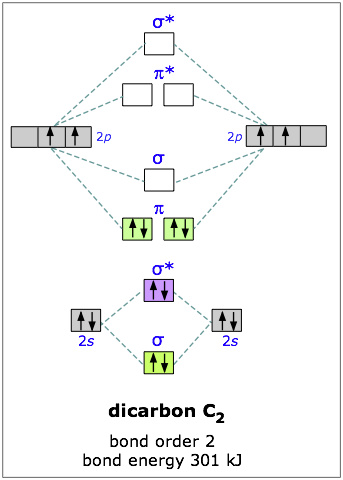
You will recall that one pair of electrons shared between two atoms constitutes a “single” chemical bond; this is Lewis’ original definition of the covalent bond. In C2 there are two paris of electrons in the π bonding orbitals, so we have what amounts to a double bond here; in other words, the bond order in dicarbon is two.
Dioxygen
The electron configuration of oxygen is 1s22s22p4. In O2, therefore, we need to accommodate twelve valence electrons (six from each oxygen atom) in molecular orbitals. As you can see from the diagram, this places two electrons in antibonding orbitals. Each of these electrons occupies a separate π* orbital because this leads to less electron-electron repulsion (Hund's Rule).
The bond energy of molecular oxygen is 498 kJ/mole. This is smaller than the 945 kJ bond energy of N2— not surprising, considering that oxygen has two electrons in an antibonding orbital, compared to nitrogen’s one.
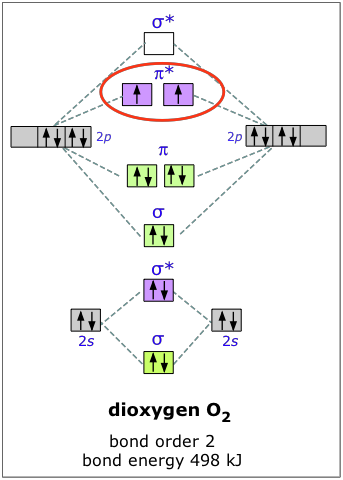
The two unpaired electrons of the dioxygen molecule give this substance an unusual and distinctive property: O2 is paramagnetic. The paramagnetism of oxygen can readily be demonstrated by pouring liquid O2 between the poles of a strong permanent magnet; the liquid stream is trapped by the field and fills up the space between the poles.
Since molecular oxygen contains two electrons in an antibonding orbital, it might be possible to make the molecule more stable by removing one of these electrons, thus increasing the ratio of bonding to antibonding electrons in the molecule. Just as we would expect, and in accord with our model, O2+ has a bond energy higher than that of neutral dioxygen; removing the one electron actually gives us a more stable molecule. This constitutes a very good test of our model of bonding and antibonding orbitals. In the same way, adding an electron to O2 results in a weakening of the bond, as evidenced by the lower bond energy of O2–. The bond energy in this ion is not known, but the length of the bond is greater, and this is indicative of a lower bond energy. These two dioxygen ions, by the way, are highly reactive and can be observed only in the gas phase.


