9.7: The Hybrid Orbital Model II
- Page ID
- 45877
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential ideas:
- Sketch out diagrams showing the hybridization and bonding in compounds containing single, double, and triple carbon-carbon bonds.
- Define sigma and pi bonds.
- Describe the hybridization and bonding in the benzene molecule.
This is a continuation of the previous page which introduced the hybrid orbital model and illustrated its use in explaining how valence electrons from atomic orbitals of s and p types can combine into equivalent shared-electron pairs known as sp, sp2, and sp3 hybrid orbitals. In this lesson, we extend this idea to compounds containing double and triple bonds, and to those in which atomic d electrons are involved (and which do not follow the octet rule.)
Hybrid types and Multiple bonds
We have already seen how sp hybridization in carbon leads to its combining power of four in the methane molecule. Two such tetrahedrally coordinated carbons can link up together to form the molecule ethane C2H6. In this molecule, each carbon is bonded in the same way as the other; each is linked to four other atoms, three hydrogens and one carbon. The ability of carbon-to-carbon linkages to extend themselves indefinitely and through all coordination positions accounts for the millions of organic molecules that are known.
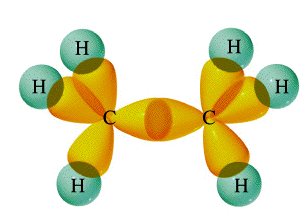
Trigonal hybridization in carbon: the double bond
Carbon and hydrogen can also form a compound ethylene (ethene) in which each carbon atom is linked to only three other atoms. Here, we can regard carbon as being trivalent. We can explain this trivalence by supposing that the orbital hybridization in carbon is in this case not sp3, but is sp2 instead; in other words, only two of the three porbitals of carbon mix with the 2s orbital to form hybrids; the remaining p-orbital, which we will call the i orbital, remains unhybridized. Each carbon is bonded to three other atoms in the same kind of plane trigonal configuration that we saw in the case of boron trifluoride, where the same kind of hybridization occurs. Notice that the bond angles around each carbon are all 120°.
This alternative hybridization scheme explains how carbon can combine with four atoms in some of its compounds and with three other atoms in other compounds. You may be aware of the conventional way of depicting carbon as being tetravalent in all its compounds; it is often stated that carbon always forms four bonds, but that sometimes, as in the case of ethylene, one of these may be a double bond. This concept of the multiple bond preserves the idea of tetravalent carbon while admitting the existence of molecules in which carbon is clearly combined with fewer than four other atoms.
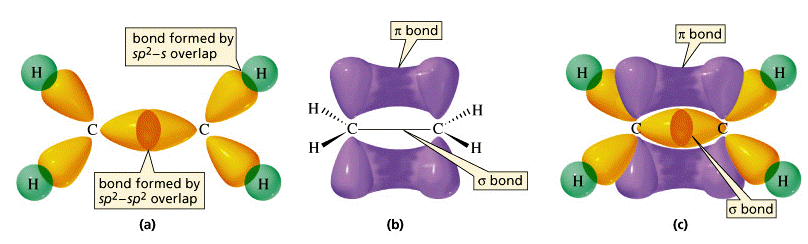
These three views of the ethylene molecule emphasize different aspects of the disposition of shared electron pairs in the various bonding orbitals of ethene (ethylene). (a) The "backbone" structure consisting of σ (sigma) bonds formed from the three sp2-hybridized orbitals on each carbon. (b) The π (pi) bonding system formed by overlap of the unhybridized pz orbital on each carbon. The π orbital has two regions of electron density extending above and below the plane of the molecule. (c) A cutaway view of the combined σ and π system.
orbital that is perpendicular to the molecular plane. These two parallel pz orbitals will interact with each other; the two orbitals merge, forming a sausage-like charge cloud (the π bond) that extends both above and below the plane of the molecule. It is the pair of electrons that occupy this new extended orbital that constitutes the “fourth” bond to each carbon, and thus the “other half” of the double bond in the molecule.More about sigma and pi bonds
The σ (sigma) bond has its maximum electron density along the line-of-centers joining the two atoms (below left). Viewed end-on, the σ bond is cylindrically symmetrical about the line-of-centers. It is this symmetry, rather than its parentage, that defines the σ bond, which can be formed from the overlap of two s-orbitals, from two p-orbitals arranged end-to-end, or from an s- and a p-orbital. They can also form when sp hybrid orbitals on two atoms overlap end-to-end.
Pi orbitals, on the other hand, require the presence of two atomic p orbitals on adjacent atoms. Most important, the charge density in the π orbital is concentrated above and below the molecular plane; it is almost zero along the line-of-centers between the two atoms. It is this perpendicular orientation with respect to the molecular plane (and the consequent lack of cylindrical symmetry) that defines the π orbital. The combination of a σ bond and a π bond extending between the same pair of atoms constitutes the double bond in molecules such as ethylene.
Carbon-carbon triple bonds: sp hybridization in acetylene
We have not yet completed our overview of multiple bonding, however. Carbon and hydrogen can form yet another compound, acetylene (ethyne), in which each carbon is connected to only two other atoms: a carbon and a hydrogen. This can be regarded as an example of divalent carbon, but is usually rationalized by writing a triple bond between the two carbon atoms.
We assume here that since two geometrically equivalent bonds are formed by each carbon, this atom must be sp-hybridized in acetylene. On each carbon, one sp hybrid bonds to a hydrogen and the other bonds to the other carbon atom, forming the σ bond skeleton of the molecule. In addition to the sp hybrids, each carbon atom has two half-occupied p orbitals oriented at right angles to each other and to the interatomic axis. These two sets of parallel and adjacent p orbitals can thus merge into two sets of π orbitals.

The triple bond in acetylene is seen to consist of one σ bond joining the line-of-centers between the two carbon atoms, and two π bonds whose lobes of electron density are in mutually-perpendicular planes. The acetylene molecule is of course linear, since the angle between the two sp hybrid orbitals that produce the s skeleton of the molecule is 180°.
Multiple bonds between unlike atoms
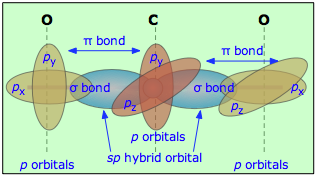
Multiple bonds can also occur between dissimilar atoms. For example, in carbon dioxide each carbon atom has two unhybridized atomic p orbitals, and each oxygen atom still has one p orbital available. When the two O-atoms are brought up to opposite sides of the carbon atom, one of the p orbitals on each oxygen forms a π bond with one of the carbon p-orbitals. In this case, sp-hybridization is seen to lead to two double bonds. Notice that the two C–O π bonds are mutually perpendicular.
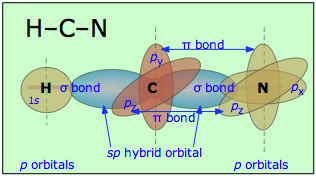
Similarly, in hydrogen cyanide, HCN, we assume that the carbon is sp-hybridized, since it is joined to only two other atoms, and is hence in a divalent state. One of the sp-hybrid orbitals overlaps with the hydrogen 1s orbital, while the other overlaps end-to-end with one of the three unhybridized p orbitals of the nitrogen atom. This leaves us with two nitrogen p-orbitals which form two mutually perpendicular π bonds to the two atomic p orbitals on the carbon. Hydrogen cyanide thus contains one single and one triple bond. The latter consists of a σ bond from the overlap of a carbon sp hybrid orbital with a nitrogen p orbital, plus two mutually perpendicular π bonds deriving from parallel atomic p orbitals on the carbon and nitrogen atoms.
The nitrate ion
Pi bond delocalization furnishes a means of expressing the structures of other molecules that require more than one electron-dot or structural formula for their accurate representation. A good example is the nitrate ion, which contains 24 electrons:
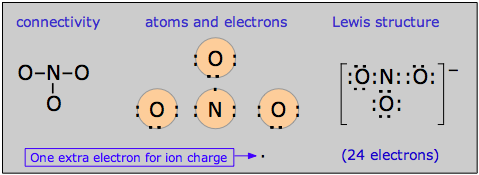
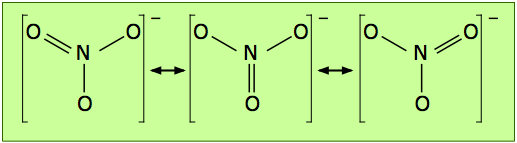
The electron-dot formula shown above is only one of three equivalent resonance structures that are needed to describe trigonal symmetry of this ion.
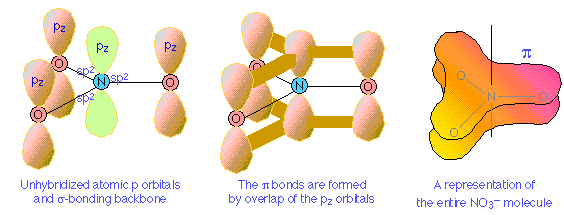
Nitrogen has three half-occupied p orbitals available for bonding, all perpendicular to one another. Since the nitrate ion is known to be planar, we are forced to assume that the nitrogen outer electrons are sp2-hybridized. The addition of an extra electron fills all three hybrid orbitals completely. Each of these filled sp2 orbitals forms a σ bond by overlap with an empty oxygen 2pz orbital; this, you will recall, is an example ofcoordinate covalent bonding, in which one of the atoms contributes both of the bonding electrons. The empty oxygen 2p orbital is made available when the oxygen electrons themselves become sp hybridized; we get three filled sp hybrid orbitals, and an empty 2p atomic orbital, just as in the case of nitrogen.
The π bonding system arises from the interaction of one of the occupied oxygen sporbitals with the unoccupied 2px orbital of the nitrogen. Notice that this, again, is a coordinate covalent sharing, except that in this instance it is the oxygen atom that donates both electrons.
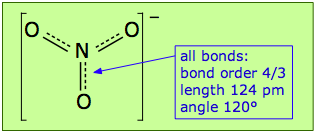
Pi bonds can form in this way between the nitrogen atom and any of the three oxygens; there are thus three equivalent π bonds possible, but since nitrogen can only form one complete π bond at a time, the π bonding is divided up three ways, so that each N–O bond has a bond order of 4/3.
Conjugated Double Bonds
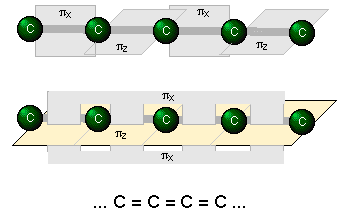
We have seen that the π bonding orbital is distinctly different in shape and symmetry from the σ bond. There is another important feature of the π bond that is of far-reaching consequence, particularly in organic and coordination chemistry. Consider, for example, an extended hydrocarbon molecule in which alternate pairs of carbon atoms are connected by double and single bonds. Each non-terminal carbon atom forms two σ bonds to two other carbons and to a hydrogen (not shown.) This molecule can be viewed as a series of ethylene units joined together end-to-end. Each carbon, being sp hybridized, still has a half-filled atomic p orbital. Since these p orbitals on adjacent carbons are all parallel, we can expect them to interact with each other to form π bonds between alternate pairs of carbon atoms as shown below.

But since each carbon atom possesses a half-filled p orbital, there is nothing unique about the π bond arrangement; an equally likely arrangement might be one in which the π bonding orbitals are shifted to neighboring pairs of carbons (middle illustration above). You will recall that when there are two equivalent choices for the arrangements single and double bonds in a molecule, we generally consider the structure to be aresonance hybrid. In keeping with this idea, we would expect the electron density in a π system of this kind to be extended or shared out evenly along the entire molecular framework, as shown in the bottom figure.
A system of alternating single and double bonds, as we have here, is called a conjugated system. Chemists say that the π bonds in a conjugated system are delocalized; they are, in effect, “smeared out” over the entire length of the conjugated part of the molecule. Each pair of adjacent carbon atoms is joined by a σ bond and "half" of a π bond, resulting in an a C-C bond order of 1.5. An even higher degree of conjugation exists in compounds containing extended (C=C)n chains. These compounds, known as cumulenes, exhibit interesting electrical properties, and whose derivatives can act as "organic wires".
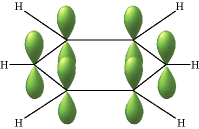
Benzene
The classic example of π bond delocalization is found in the cyclic molecule benzene (C6H6) which consists of six carbon atoms bound together in a hexagonal ring. Each carbon has a single hydrogen atom attached to it. The lines in this figure represent the σ bonds in benzene. The basic ring structure is composed of σ bonds formed from overlap of sp2 hybrid orbitals on adjacent carbon atoms. The unhybridized carbon pz orbitals project above and below the plane of the ring. They are shown here as they might appear if they did not interact with one another.
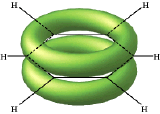
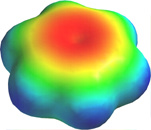
But what happens, of course, is that the lobes of these atomic orbitals meld together to form circular rings of electron density above and below the plane of the molecule. The two of these together constitute the "second half" of the carbon-carbon double bonds in benzene. This computer-generated plot of electron density in the benzene molecule is derived from a more rigorous theory that does not involve hybrid orbitals; the highest electron density (blue) appears around the periphery of the ring, while the lowest (red) is in the "doughnut hole" in the center.
Hybrids involving d orbitals
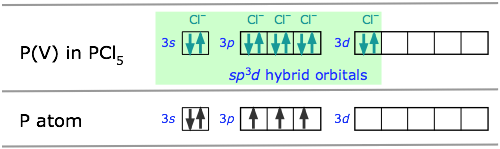
In atoms that are below those in the first complete row of the periodic table, the simple octet rule begins to break down. For example, we have seen that PCl3 does conform to the octet rule but PCl5 does not. We can describe the bonding in PCl3 very much as we do NH3: four sp3-hybridized orbitals, three of which are shared with electrons from other atoms and the fourth containing a nonbonding pair.
Pentagonal bipyramid molecules: sp3d hybridization
hybrid orbitals directed toward the corners of a trigonal bipyramid, as is predicted by VSEPR theory.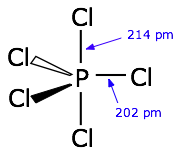
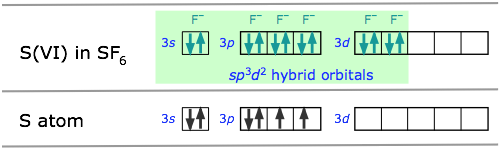
Octahedral coordination: sp3d2 hybridization
The molecule sulfur hexafluoride SF6 exemplifies one of the most common types of d-orbital hybridization. The six bonds in this octahedrally-coordinated molecule are derived from mixing six atomic orbitals into a hybrid set. The easiest way to understand how these come about is to imagine that the molecule is made by combining an imaginary S6+ ion (which we refer to as the S(VI) valence state) with six F– ions to form the neutral molecule. These now-empty 3s and 3p orbitals then mix with two 3d orbitals to form the sp3d2 hybrids.
Some of the most important and commonly encountered compounds which involve the dorbitals in bonding are the transition metal complexes. The term “complex” in this context means that the molecule is composed of two or more kinds of species, each of which can have an independent existence.
Square-planar molecules: dsp2 hybridization
For example, the ions Pt2+ and Cl– can form the ion [PtCl4]2–. To understand the hybridization scheme, it helps to start with the neutral Pt atom, then imagine it losing two electrons to become an ion, followed by grouping of the two unpaired 5d electrons into a single d orbital, leaving one vacant.This vacant orbital, along with the 6s and two of the 6p orbitals, can then accept an electron pair from four chlorines.
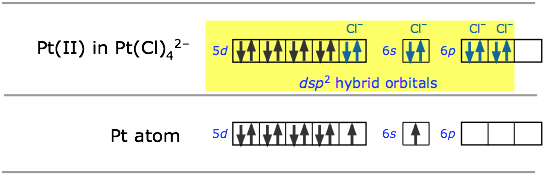
All of the four-coordinated molecules we have discussed so far have tetrahedral geometry around the central atom. Methane, CH4, is the most well known example. It may come as something as a surprise, then, to discover that the tetrachlorplatinum (II) ion [PtCl4]2– has an essentially two-dimensional square-planar configuration. This type of bonding pattern is quite common when the parent central ion (Pt2+ in this case) contains only eight electrons in its outmost d-subshell.
Octahedral coordination: sp3d2 and d2sp3
Many of the most commonly encountered transition metal ions accept electron pairs from donors such as CN– and NH3 (or lacking these, even from H2O) to form octahedral coordination complexes. The hexaminezinc(II) cation depicted below is typical.
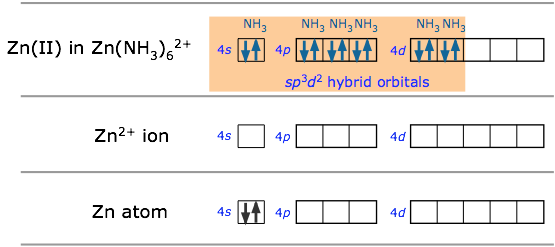
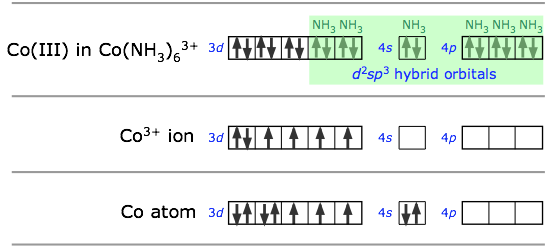
In sp3d2 hybridization the bonding orbitals are derived by mixing atomic orbitals having the same principal quantum number (n = 4 in the preceding example). A slightly different arrangement, known as d2sp3 hybridization, involves d orbitals of lower principal quantum number. This is possible because of the rather small energy differences between the d orbitals in one “shell” with the s and p orbitals of the next higher one — hence the term “inner orbital” complex which is sometimes used to describe ions such as hexaminecobalt(III), shown below.. Both arrangements produce octahedral coordination geometries.
In some cases, the same central atom can form either inner or outer complexes depending on the particular ligand and the manner in which its electrostatic field affects the relative energies of the different orbitals.Thus the hexacyanoiron(II) ion utilizes the iron 3d orbitals, whereas hexaaquoiron(II) achieves a lower energy by accepting two H2O molecules in its 4d orbitals.
complexes.png?revision=1&size=bestfit&width=545&height=372)
Final remarks about hybrid orbitals
As is the case with any scientific model, the hybridization model of bonding is useful only to the degree to which it can predict phenomena that are actually observed. Most models contain weaknesses that place limits on their general applicability. The need for caution in accepting this particular model is made more apparent when we examine the shapes of the molecules below the first full row of the periodic table. For example, we would expect the bonding in hydrogen sulfide to be similar to that in water, with tetrahedral geometry around the sulfur atom. Experiments, however, reveal that the H–S–H bond angle is only 92°. Hydrogen sulfide thus deviates much more from tetrahedral geometry than does water, and there is no apparent and clear reason why it should. It is certainly difficult to argue that electron-repulsion between the two nonbonding orbitals is pushing the H–S bonds closer together (as is supposed to happen to the H–O bonds in water); many would argue that this repulsion would be less in hydrogen sulfide than in water, since sulfur is a larger atom and is hence less electronegative.
orbitals does not apply to H2S. It looks like the “simple” explanation that bonding occurs through two half occupied atomic p orbitals 90° apart comes closer to the mark. Perhaps hybridization is not an all-or-nothing phenomenon; perhaps the two 3p orbitals are substantially intact in hydrogen sulfide, or are hybridized only slightly. In general, the hybridization model does not work very well with nonmetallic elements farther down in the periodic table, and there is as yet no clear explanation why. We must simply admit that we have reached one of the many points in chemistry where our theory is not sufficiently developed to give a clear and unequivocal answer. This does not detract, however, from the wide usefulness of the hybridization model in elucidating the bond character and bond shapes in the millions of molecules based on first-row elements, particularly of carbon.Are hybrid orbitals real?
The justification we gave for invoking hybridization in molecules such as BeH2, BF3 and CH4 was that the bonds in each are geometrically and chemically equivalent, whereas the atomic s- and p-orbitals on the central atoms are not. By combining these into new orbitals of sp, sp2 and sp3 types we obtain the required number of completely equivalent orbitals. This seemed easy enough to do on paper; we just drew little boxes and wrote “sp2” or whatever below them. But what is really going on here?
The full answer is beyond the scope of this course, so we can only offer the following very general explanation. First, recall what we mean by “orbital”: a mathematical function ψ having the character of a standing wave whose square ψ2 is proportional to the probability of finding the electron at any particular location in space. The latter, the electron density distribution, can be observed (by X-ray scattering, for example), and in this sense is the only thing that is “real”.
A given standing wave (ψ-function) can be synthesized by combining all kinds of fundamental wave patterns (that is, atomic orbitals) in much the same way that a color we observe can be reproduced by combining different sets of primary colors in various proportions. In neither case does it follow that these original orbitals (or colors) are actually present in the final product. So one could well argue that hybrid orbitals are not “real”; they simply turn out to be convenient for understanding the bonding of simple molecules at the elementary level, and this is why we use them.
An alternative to hybrids: the Bent-Bond model
It turns out, in fact, that the electron distribution and bonding in ethylene can be equally well described by assuming no hybridization at all. The "bent bond" model requires only that the directions of some of the atomic-p orbitals be distorted sufficiently to provide the overlap needed for bonding; these are sometimes referred to as "banana bonds".
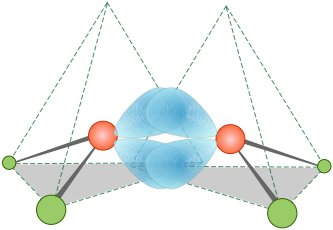
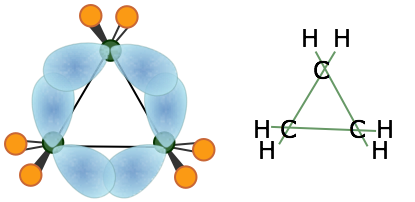

The smallest of the closed-ring hydrocarbons is cyclopropane, a planar molecule in which the C–C bond angles are 120°— quite a departure from the tetrahedral angle of 109.5° associated with sp3 hybridization! Theoretical studies suggest that the bent-bond model does quite well in predicting its properties.


