8.5: Colligative Properties - Osmotic Pressure
- Page ID
- 3570
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define a semipermeable membrane in the context of osmotic flow.
- Explain, in simple terms, what fundamental process "drives" osmotic flow.
- What is osmotic pressure, and how is it measured?
- Osmotic pressure can be a useful means of estimating the molecular weight of a substance, particularly if its molecular weight is quite large. Explain in your own words how this works.
- What is reverse osmosis, and what is its principal application?
- Explain the role of osmotic pressure in food preservation, and give an example.
- Describe the role osmosis plays in the rise of water in plants (where is the semipermeable membrane?), and why it cannot be the only cause in very tall trees.
Osmosis is the process in which a liquid passes through a membrane whose pores permit the passage of solvent molecules but are too small for the larger solute molecules to pass through.
Semipermeable Membranes and Osmotic flow
Figure \(\PageIndex{1}\) shows a simple osmotic cell. Both compartments contain water, but the one on the right also contains a solute whose molecules (represented by green circles) are too large to pass through the membrane. Many artificial and natural substances are capable of acting as semi-permeable membranes. The walls of most plant and animal cells fall into this category.
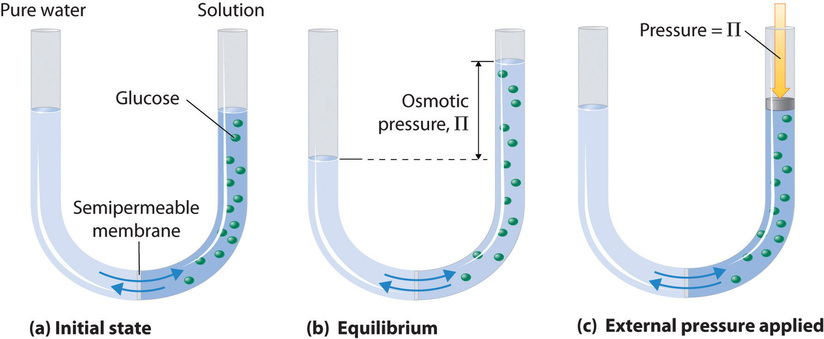
If the cell is set up so that the liquid level is initially the same in both compartments, you will soon notice that the liquid rises in the left compartment and falls in the right side, indicating that water molecules from the right compartment are migrating through the semipermeable membrane and into the left compartment. This migration of the solvent is known as osmotic flow, or simply osmosis.
The escaping tendency of a substance from a phase increases with its concentration in the phase. What is the force that drives the molecules through the membrane? This is a misleading question, because there is no real “force” in the physical sense other than the thermal energies all molecules possess. Osmosis is a consequence of simple statistics: the randomly directed motions of a collection of molecules will cause more to leave a region of high concentration than return to it; the escaping tendency of a substance from a phase increases with its concentration in the phase.
Diffusion and Osmotic Flow
Suppose you drop a lump of sugar into a cup of tea, without stirring. Initially there will be a very high concentration of dissolved sugar at the bottom of the cup, and a very low concentration near the top. Since the molecules are in random motion, there will be more sugar molecules moving from the high concentration region to the low concentration region than in the opposite direction. The motion of a substance from a region of high concentration to one of low concentration is known as diffusion. Diffusion is a consequence of a concentration gradient (which is a measure of the difference in escaping tendency of the substance in different regions of the solution).
There is really no special force on the individual molecules; diffusion is purely a consequence of statistics. Osmotic flow is simply diffusion of a solvent through a membrane impermeable to solute molecules. Now take two solutions of differing solvent concentration, and separate them by a semipermeable membrane (Figure \(\PageIndex{2}\)). Being semipermeable, the membrane is essentially invisible to the solvent molecules, so they diffuse from the high concentration region to the low concentration region just as before. This flow of solvent constitutes osmotic flow, or osmosis.
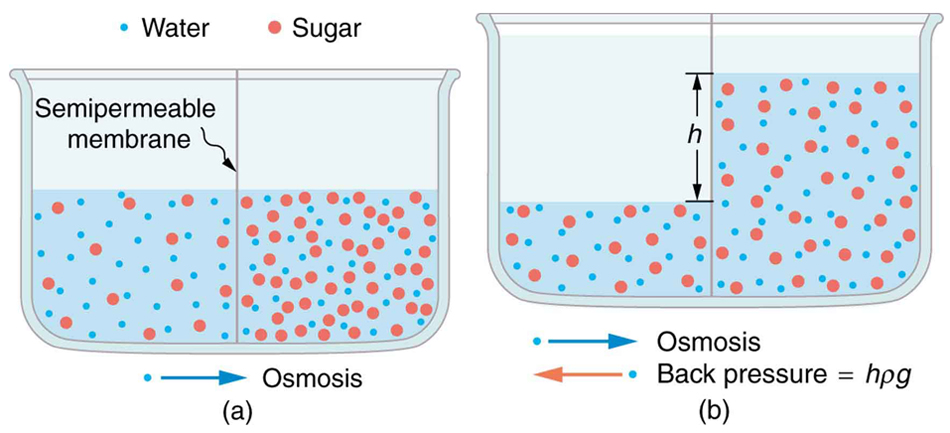
Figure \(\PageIndex{2}\): Osmosis osmotic flow(a) Two sugar-water solutions of different concentrations, separated by a semipermeable membrane that passes water but not sugar. Osmosis will be to the right, since water is less concentrated there. (b) The fluid level rises until the back pressure ρgh equals the relative osmotic pressure; then, the net transfer of water is zero. (CC-BY; OpenStax).
Figure \(\PageIndex{2}\) shows water molecules (blue) passing freely in both directions through the semipermeable membrane, while the larger solute molecules remain trapped in the left compartment, diluting the water and reducing its escaping tendency from this cell, compared to the water in the right side. This results in a net osmotic flow of water from the right side which continues until the increased hydrostatic pressure on the left side raises the escaping tendency of the diluted water to that of the pure water at 1 atm, at which point osmotic equilibrium is achieved.
Osmotic flow is simply diffusion of a solvent through a membrane impermeable to solute molecules.
In the absence of the semipermeable membrane, diffusion would continue until the concentrations of all substances are uniform throughout the liquid phase. With the semipermeable membrane in place, and if one compartment contains the pure solvent, this can never happen; no matter how much liquid flows through the membrane, the solvent in the right side will always be more concentrated than that in the left side. Osmosis will continue indefinitely until we run out of solvent, or something else stops it.
Osmotic equilibrium and osmotic pressure
One way to stop osmosis is to raise the hydrostatic pressure on the solution side of the membrane. This pressure squeezes the solvent molecules closer together, raising their escaping tendency from the phase. If we apply enough pressure (or let the pressure build up by osmotic flow of liquid into an enclosed region), the escaping tendency of solvent molecules from the solution will eventually rise to that of the molecules in the pure solvent, and osmotic flow will case. The pressure required to achieve osmotic equilibrium is known as the osmotic pressure. Note that the osmotic pressure is the pressure required to stop osmosis, not to sustain it.
Osmotic pressure is the pressure required to stop osmotic flow It is common usage to say that a solution “has” an osmotic pressure of "x atmospheres". It is important to understand that this means nothing more than that a pressure of this value must be applied to the solution to prevent flow of pure solvent into this solution through a semipermeable membrane separating the two liquids.
Osmotic Pressure and Solute Concentration
The Dutch scientist Jacobus Van't Hoff (1852-1911) was one of the giants of physical chemistry. He discovered this equation after a chance encounter with a botanist friend during a walk in a park in Amsterdam; the botanist had learned that the osmotic pressure increases by about 1/273 for each degree of temperature increase. van’t Hoff immediately grasped the analogy to the ideal gas law. The osmotic pressure \(\Pi\) of a solution containing \(n\) moles of solute particles in a solution of volume \(V\) is given by the van 't Hoff equation:
\[\Pi = \dfrac{nRT}{V} \label{8.4.3}\]
in which
- \(R\) is the gas constant (0.0821 L atm mol–1 K–1) and
- \(T\) is the absolute temperature.
In contrast to the need to employ solute molality to calculate the effects of a non-volatile solute on changes in the freezing and boiling points of a solution, we can use solute molarity to calculate osmotic pressures.
Note that the fraction \(n/V\) corresponds to the molarity (\(M\)) of a solution of a non-dissociating solute, or to twice the molarity of a totally-dissociated solute such as \(NaCl\). In this context, molarity refers to the summed total of the concentrations of all solute species. Hence, Equation \ref{8.4.3} can be expressed as
\[\Pi =MRT \label{8.4.3B}\]
Recalling that \(\Pi\) is the Greek equivalent of P, the re-arranged form \(\Pi V = nRT\) of the above equation should look familiar. Much effort was expended around the end of the 19th century to explain the similarity between this relation and the ideal gas law, but in fact, the Van’t Hoff equation turns out to be only a very rough approximation of the real osmotic pressure law, which is considerably more complicated and was derived after van 't Hoff's formulation. As such, this equation gives valid results only for extremely dilute ("ideal") solutions.
According to the Van't Hoff equation, an ideal solution containing 1 mole of dissolved particles per liter of solvent at 0° C will have an osmotic pressure of 22.4 atm.
Sea water contains dissolved salts at a total ionic concentration of about 1.13 mol L–1. What pressure must be applied to prevent osmotic flow of pure water into sea water through a membrane permeable only to water molecules?
Solution
This is a simple application of Equation \ref{8.4.3B}.
\[ \begin{align*} \Pi &= MRT \\[4pt] &= (1.13\; mol /L)(0.0821\; L \,atm \,mol^{–1}\; K^{–1})(298\; K) \\[4pt] &= 27.6\; atm \end{align*}\]
Molecular Weight Determination by Osmotic Pressure
Since all of the colligative properties of solutions depend on the concentration of the solvent, their measurement can serve as a convenient experimental tool for determining the concentration, and thus the molecular weight, of a solute. Osmotic pressure is especially useful in this regard, because a small amount of solute will produce a much larger change in this quantity than in the boiling point, freezing point, or vapor pressure. even a 10–6 molar solution would have a measurable osmotic pressure. Molecular weight determinations are very frequently made on proteins or other high molecular weight polymers. These substances, owing to their large molecular size, tend to be only sparingly soluble in most solvents, so measurement of osmotic pressure is often the only practical way of determining their molecular weights.
The osmotic pressure of a benzene solution containing 5.0 g of polystyrene per liter was found to be 7.6 torr at 25°C. Estimate the average molecular weight of the polystyrene in this sample.
Solution:
osmotic pressure:
\[ \begin{align*} \Pi &= \dfrac{7.6\, torr}{760\, torr\, atm^{–1}} \\[4pt] &= 0.0100 \,atm \end{align*} \]
Using the form of the van 't Hoff equation (Equation \ref{8.4.3}), PV = nRT, the number of moles of polystyrene is
n = (0.0100 atm)(1 L) ÷ (0.0821 L atm mol–1 K–1)(298 K) = 4.09 x 10–4 mol
Molar mass of the polystyrene:
(5.0 g) ÷ (4.09 x 10–4 mol) = 12200 g mol–1.
The experiment to demonstrate this is quite simple: pure solvent is introduced into one side of a cell that is separated into two parts by a semipermeable membrane. The polymer solution is placed in the other side, which is enclosed and connected to a manometer or some other kind of pressure gauge. As solvent molecules diffuse into the solution cell the pressure builds up; eventually this pressure matches the osmotic pressure of the solution and the system is in osmotic equilibrium. The osmotic pressure is read from the measuring device and substituted into the van’t Hoff equation to find the number of moles of solute.


