8.2: Thermodynamics of Solutions
- Page ID
- 3574
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential ideas:
- Describe the two fundamental processes that must occur whenever a solute dissolves in a solvent, and discuss the effects of the absorption or release of energy on the extent of these processes.
- Another factor entering into the process of solution formation is the increase (or occasionally, the decrease) in the entropy — that is, the degree to which thermal energy is dispersed or "diluted". Explain this in your own terms.
- Explain how the adage "like dissolves like" reflects the effects mentioned above. What is the principal physical property of a molecule that defines this "likeness"?
- What do we mean when we describe a liquid such as water as "associated"? Explain how this relates to the the solubility of solutes in such liquids.
You may recall that in the earlier unit on phase equilibria, we pointed out that aggregations of molecules that are more disordered tend to be the ones that are favored at higher temperature, whereas those that possess the lowest potential energy are favored at lower temperatures. This is a general principle that applies throughout the world of matter; the stable form at any given temperature will always be that which leads to the best balance between low potential energy and high molecular disorder. To see how these considerations are applied to solutions, think about the individual steps that must be carried out when a solute is dissolved in a solvent:

- If the solute is a solid or liquid, it must first be dispersed — that is, its molecular units must be pulled apart. This requires energy, and so this step always works against solution formation.

- The solute must then be introduced into the solvent. Whether this is energetically favorable or unfavorable depends on the nature of the solute and solvent. If the solute is A and the solvent is B, then what is important is the strength of the attractive forces between A-A and B-B molecules, compared to those between A-B pairs; if the latter are greater, then the potential energy will be lower when the substances are mixed and solution formation will be favored.
If step 2 releases more energy than is consumed in step 1, this will favor solution formation, and we can generally expect the solute to be soluble in the solvent. Even if the dissolution process is slightly endothermic, there is a third important factor, the entropy increase, that will very often favor the dissolved state.
Entropy of Solution
As anyone who has shuffled a deck of cards knows, disordered arrangements of objects are statistically more favored simply because there are more ways in which they can be realized. And as the number of objects increases, the more does statistics govern their most likely arrangements. The numbers of objects (molecules) we deal with in Chemistry is so huge that their tendency to become as spread out as possible becomes overwhelming. However, in doing so, the thermal energy they carry with them is also spread and dispersed, so the availability of this energy, as measured by the temperature, is also of importance. Chemists use the term "entropy" to denote this aspect of molecular randomness.
Readers of this section who have had some exposure to thermodynamics will know that solubility, like all equilibria, is governed by the Gibbs free energy change for the process, which incorporates the entropy change at a fundamental level. A proper understanding of these considerations requires some familiarity with thermodynamics, which most students do not encounter until well into their second semester of Chemistry. If you are not there yet, do not despair; you are hereby granted temporary permission to think of molecular "disorder" and entropy simply in terms of "spread-outedness".
Thus in the very common case in which a small quantity of solid or liquid dissolves in a much larger volume of solvent, the solute becomes more spread out in space, and the number of equivalent ways in which the solute can be distributed within this volume is greatly increased. This is the same as saying that the entropy of the solute increases.
If the energetics of dissolution are favorable, this increase in entropy means that the conditions for solubility will always be met. Even if the energetics are slightly endothermic, the entropy effect can still allow the solution to form, although perhaps limiting the maximum concentration that can be achieved. In such a case, we may describe the solute as being slightly soluble in a certain solvent. What this means is that a greater volume of solvent will be required to completely dissolve a given mass of solute.
Enthalpy of Solution
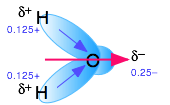
Polar molecules are those in which electric charge is distributed asymmetrically. The most familiar example is ordinary water, in which the highly electronegative oxygen atom pulls part of the electric charge cloud associated with each O–H bond closer to itself. Although the H2O molecule is electrically neutral overall, this charge imbalance gives rise to a permanent electric dipole moment.
Chemists use the term "Associated" liquids to refer to liquids in which the effects of hydrogen bonding dominate the local structure. Water is the most important of these, but ammonia NH3 and hydrogen cyanide HCN are other common examples.
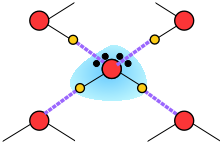
Thus liquid water consists of an extended network of H2O molecules linked together by dipole-dipole attractions that we call hydrogen bonds. Because these are much weaker than ordinary chemical bonds, they are continually being disrupted by thermal forces. As a result, the extended structure is highly disordered (in contrast to that of solid ice) and continually changing.
When a solute molecule is introduced into an associated liquid, a certain amount of energy must be expended in order to break the local hydrogen-bond structure and make space for the new molecule. If the solute is itself an ion or a polar molecule, new ion-dipole or dipole-dipole attractions come into play. In favorable cases these may release sufficient potential energy to largely compensate for the energy required to incorporate the solute into the structure.
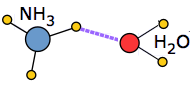
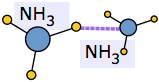
An extreme example of this occurs when ammonia dissolves in water. Each NH3 molecule can form three hydrogen bonds, so the resulting solution is even more hydrogen-bonded than is pure water — accounting for the considerable amount of heat released in the process and the extraordinarily large solubility of ammonia in water.
Nonpolar solutes are Sparingly Soluble in Water: The Hydrophobic effect
When a nonpolar solute such as oxygen or hexane is introduced into an associated liquid, we might expect that the energy required to break the hydrogen bonds to make space for the new molecule is not compensated by the formation of new attractive interactions, suggesting that the process will be energetically unfavorable. We can therefore predict that solutes of these kinds will be only sparingly soluble in water, and this is indeed the case.
It turns out, however, that this is not an entirely correct explanation for the small solubility of non polar solutes in water. It is now known that the H2O molecules that surround a non-polar intruder and find themselves unable to form energy-lowering polar or hydrogen-bonded interactions with it will rearrange themselves into a configuration that maximizes the hydrogen bonding between the water molecules themselves. In doing so, this creates a cage-like shell around the solute molecule. In terms of the energetics of the process, these new H2O-H2O interactions largely compensate for the lack of solute-H2O interactions.

However, this shell of highly organized water molecules exacts its own toll on the solubility by reducing the entropy of the system. Dissolution of a solute normally increases the entropy by spreading the solute molecules (and the thermal energy they contain) through the larger volume of the solvent. But in this case, the H2O molecules within the highly structured shell surrounding the solute molecule are themselves constrained to this location, and their number is sufficiently great to reduce the entropy by far more than the dissolved solute increases it.
The implications of the hydrophobic effect extend far beyond the topic of solubility. It governs the way that proteins fold, the formation of soap bubbles, and the formation of cell membranes. The small solubility of a non polar solute in an associated liquid such as water results more from the negative entropy change rather than from energetic considerations. This phenomenon is known as the hydrophobic effect. In the next section, we will explore the ways in which these energy-and-entropy considerations come together in various kinds of solutions.


