8.2.2B: Solutions of Gaseous Solutes in Liquid Solvents

Learning Objectives

Make sure you thoroughly understand the following essential ideas:

• Explain why, in contrast, gases tend to be only slightly soluble in liquids and solids. And why are some combinations, such as the dissolution of ammonia or hydrogen chloride in water, significant exceptions to this rule?
• State Henry's law and explain
• Why do fish in rivers and streams sometimes become asphyxiated (oxygen-starved) in hot weather?

Solutions of Gases in Liquids

Gases dissolve in liquids, but usually only to a small extent. When a gas dissolves in a liquid, the ability of the gas molecules to move freely throughout the volume of the solvent is greatly restricted. If this latter volume is small, as is often the case, the gas is effectively being compressed. Both of these effects amount to a decrease in the entropy of the gas that is not usually compensated by the entropy increase due to mixing of the two kinds of molecules. Such processes greatly restrict the solubility of gases in liquids.

liquid solvent, solute →	gas
energy to disperse solute	nil
energy to introduce into solvent	medium to large
increase in entropy	negative
miscibility	usually very limited

Solubility of gases in water

One important consequence of the entropy decrease when a gas dissolves in a liquid is that the solubility of a gas decreases at higher temperatures; this is in contrast to most other situations, where a rise in temperature usually leads to increased solubility. Bringing a liquid to its boiling point will completely remove a gaseous solute. Some typical gas solubilities, expressed in the number of moles of gas at 1 atm pressure that will dissolve in a liter of water at 25° C, are given below:

solute	formula	solubility, mol L^–1 atm^–1
ammonia	NH3	57
carbon dioxide	CO2	0.0308
methane	CH4	0.00129
nitrogen	N2	0.000661
oxygen	O2	0.00126
sulfur dioxide	SO2	1.25

As we indicated above, the only gases that are readily soluble in water are those whose polar character allows them to interact strongly with it.

Ammonia is remarkably soluble in water

Inspection of the above table reveals that ammonia is a champion in this regard. At 0° C, one liter of water will dissolve about 90 g (5.3 mol) of ammonia. The reaction of ammonia with water according to

\[\ce{NH_3 + H_2O → NH_4^{+} + OH^{–}}\]

makes no significant contribution to its solubility; the equilibrium lies heavily on the left side (as evidenced by the strong odor of ammonia solutions). Only about four out of every 1000 NH₃molecules are in the form of ammonium ions at equilibrium. This is truly impressive when one calculates that this quantity of NH₃ would occupy (5.3 mol) × (22.4 L mol^–1) = 119 L at STP. Thus one volume of water will dissolve over 100 volumes of this gas. It is even more impressive when you realize that in order to compress 119 L of an ideal gas into a volume of 1 L, a pressure of 119 atm would need to be applied! This, together with the observation that dissolution of ammonia is accompanied by the liberation of a considerable amount of heat, tells us that the high solubility of ammonia is due to the formation of more hydrogen bonds (to H₂O) than are broken within the water structure in order to accommodate the NH₃ molecule.

If we actually compress 90 g of pure NH₃ gas to 1 L, it will liquefy, and the vapor pressure of the liquid would be about 9 atm. In other words, the escaping tendency of NH₃ molecules from H₂O is only about 1/9th of what it is from liquid NH₃. One way of interpreting this is that the strong intermolecular (dipole-dipole) attractions between NH₃ and the solvent H₂O give rise to a force that has the effect of a negative pressure of 9 atm.

The Ammonia Fountain

This classic experiment nicely illustrates the high solubility of gaseous ammonia in water. A flask fitted with a tube as shown is filled with ammonia gas and inverted so that the open end of tube is submerged in a container of water. A small amount of water is pushed up into the flask to get the process started. As the gas dissolves in the water, its pressure is reduced, creating a partial vacuum that draws additional water into the flask. The effect can be made more dramatic by adding an indicator dye such as phenolphthalein to the water, which turns pink as the water emerges from the "fountain" and becomes alkaline.

In old textbooks, ammonia's extraordinarily high solublility in water was incorrectly attributed to the formation of the non-existent compound "ammonium hydroxide" NH₄OH. Although this formula is still occasionally seen, the name ammonium hydroxide is now used as a synonym for "aqueous ammonia" whose formula is simply NH₃(aq).

As can also be seen in the above table, the gases CO₂ and SO₂ also exhibit higher solubilities in water. The main product in each case is a loosely-bound hydrate of the gas, denoted by CO₂(aq) or SO₂(aq). A very small fraction of the hydrate CO₂·H₂O then combines to form carbonic acid H₂CO₃.

Solubility of gases decreases with Temperature

Recall that entropy is a measure of the ability of thermal energy to spread and be shared and exchanged by molecules in the system. Higher temperature exerts a kind of multiplying effect on a positive entropy change by increasing the amount of thermal energy available for sharing. Have you ever noticed the tiny bubbles that form near the bottom of a container of water when it is placed on a hot stove? These bubbles contain air that was previously dissolved in the water, but reaches its solubility limit as the water is warmed. You can completely rid a liquid of any dissolved gases (including unwanted ones such as Cl₂ or H₂S) by boiling it in an open container.

This is quite different from the behavior of most (but not all) solutions of solid or liquid solutes in liquid solvents. The reason for this behavior is the very large entropy increase that gases undergo when they are released from the confines of a condensed phase .

Solubility of Oxygen in water

Fresh water at sea level dissolves 14.6 mg of oxygen per liter at 0°C and 8.2 mg/L at 25°C. These saturation levels ensure that fish and other gilled aquatic animals are able to extract sufficient oxygen to meet their respiratory needs. But in actual aquatic environments, the presence of decaying organic matter or nitrogenous runoff can reduce these levels far below saturation. The health and survival of these organisms is severely curtailed when oxygen concentrations fall to around 5 mg/L.

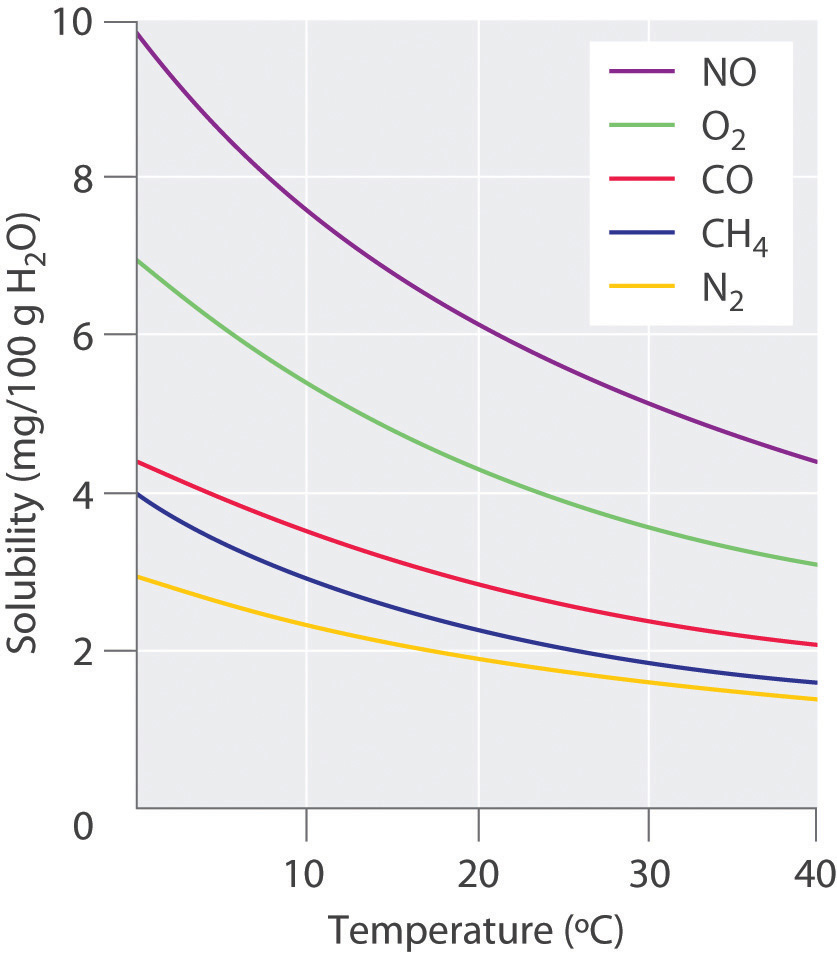
The temperature dependence of the solubility of oxygen in water is an important consideration for the well-being of aquatic life; thermal pollution of natural waters (due to the influx of cooling water from power plants) has been known to reduce the dissolved oxygen concentration to levels low enough to kill fish. The advent of summer temperatures in a river can have the same effect if the oxygen concentration has already been partially depleted by reaction with organic pollutants.

Solubility of gases increases with pressure: Henry's Law

The pressure of a gas is a measure of its "escaping tendency" from a phase. So it stands to reason that raising the pressure of a gas in contact with a solvent will cause a larger fraction of it to "escape" into the solvent phase. The direct-proportionality of gas solubility to pressure was discovered by William Henry (1775-1836) and is known as Henry's Law. It is usually written as

\[P = k_H C \label{7b.2.1}\]

with

• \(P\) is the partial pressure of the gas above the liquid,
• \(C\) is the concentration of gas dissolved in the liquid, and
• \(k_H\) is the Henry's law constant, which can be expressed in various units, and in some instances is defined in different ways, so be very careful to note these units when using published values.

For Table 7b.2.X, k_H is given as

\[ k_H = \dfrac{\text{partial pressure of gas in atm}}{\text{concentration in liquid} \; mol \;L^{–1}}\]

Table 7b.2.X: Henry's law constants in water at 25° C, L atm mol^–1

gas	He	N2	O2	CO2	CH4	NH3
KH	2703	1639	769	29.4	0.00129	57

Example \(\PageIndex{1}\)

Some vendors of bottled waters sell pressurized "oxygenated water" that is (falsely) purported to enhance health and athletic performance by supplying more oxygen to the body.

1. How many moles of O₂ will be in equilibrium with one liter of water at 25° C when the partial pressure of O₂ above the water is 2.0 atm?
2. How many mL of air (21% O₂ v/v) must you inhale in order to introduce an equivalent quantity of O₂ into the lungs (where it might actually do some good?)

Solution:

1. Solving Henry's law for the concentration, we get

\[C = \dfrac{P}{k_H} = \dfrac{2.0\; atm}{769\; L\; atm \;mol^{–1}} = 0.0026\; mol\; L^{–1}\]

1. At 25° C, 0.0026 mol of O₂ occupies (22.4 L) × (.0026 mol) × (298/273) = 0.063 L. The equivalent volume of air would be (0.063 L) (.21) = 0.303 L. Given that the average tidal volume of the human lung is around 400 mL, this means that taking one extra breath would take in more O₂ than is present in 1 L of "oxygenated water".

Carbonated beverages: the history of "Fizz-ics"

Artificially carbonated water was first prepared by Joseph Priestley (who later discovered oxygen) in 1767 and was commercialized in 1783 by Joseph Schweppe, a Swiss-German jeweler. Naturally-carbonated spring waters have long been reputed to have curative values, and these became popular tourist destinations in the 19th century. The term "seltzer water" derives from one such spring in Niederselters, Germany. Of course, carbonation produced by fermentation has been known since ancient times. The tingling sensation that carbonated beverages produce in the mouth comes from the carbonic acid produced when bubbles of carbon dioxide come into contact with the mucous membranes of the mouth and tongue:

\[CO_2 + H_2O → H_2CO_3\]