Temperature Effects on the Solubility of Gases
- Page ID
- 1615
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As with all processes under constant pressure and constant temperature, dissolving a solution into solution will occur only if \(\Delta G_{total} < 0\).
\[\Delta G_{sol} = \Delta H_{sol} - T\Delta S_{sol} < 0\label{eq1}\]
For dissolving solids in liquids, \(\Delta S_{sol} > 0\), but for dissolving gases solutes, the entropy of solution is negative (\(\Delta S _{sol} < 0\)) since the entropy of the gas phase solute is appreciably greater than the entropy of that solute in solution. Consequently, the only way that \(\Delta G_{sol}<0\) for a dissolving a gas in solution is if the solution process is exothermic (i.e., \(\Delta H_{sol}<0\)). This occurs due to the enthalpy differences from making and breaking intermolecular interactions in the solvent and solution. There are three basic steps involved in dissolving a solute from a condensed state (or a non-ideal gas) into a solution each with a corresponding enthalpy change.
Dissolution can be viewed as occurring in three steps:
- Breaking solute-solute attractions (endothermic), i.e., lattice energy in salts (\(\Delta H_{\text{solute-solute}}>0\)).
- Breaking solvent-solvent attractions (endothermic), i.e., hydrogen bonding and dipole-dipole interactions in water (\(\Delta H_{\text{solvent-solvent}}>0\).
- Forming solvent-solute attractions (exothermic), i.e., solvation energy (\(\Delta H_{\text{solute-solvent}}<0\)).
The enthalpy of solution \(\Delta H_{sol}\) is the sum of these three individual steps.
\[ \Delta H_{sol} = \Delta H_{\text{solute-solute}} + \Delta H_{\text{solvent-solvent}} + \Delta H_{\text{solute-solvent}} \label{eq2}\]
For solids solutes, \(\Delta H_{\text{solute-solute}}\) is just the lattice energy of the solute, but for gases that follow the ideal gas equation of state, the enthalpy change associated with Step 1 is zero.
\[\Delta H_{\text{solute-solute}} (gas) =0 \]
This is because are no intermolecular interactions exist in ideal gases (van der Waals gases will differ as expected).
Solubility of Gases in Polar Solvents
In polar solvents like water, \(\Delta H_{\text{solute-solvent}} > \Delta H_{\text{solvent-solvent}}\), so the dissolution of most gases is exothermic (i.e., \(\Delta H_{sol} <0\)). Hence, when a gas dissolves in a liquid solvent, thermal energy is released which warms both the system (the solution) and the surroundings.
\[\ce{ solute (gas) + water (l) \rightleftharpoons solute (aq) + water (aq)} + \Delta \label{eq4}\]
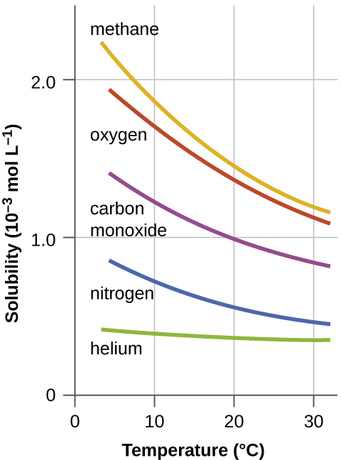
where \(Delta\) is thermal enegy. Consequently, the solubility of a gas is dependent on temperature (Figure \(\PageIndex{1}\)). The solubility of gases in liquids decreases with increasing temperature. Conversely, adding heat to the solution provides thermal energy that overcomes the attractive forces between the gas and the solvent molecules, thereby decreasing the solubility of the gas; pushes the reaction in Equation \ref{eq4} to the left. The thermodynamic perspective is that at elevated temperatures, the negative entropy term in Equation \ref{eq1} will dominate the enthalpic term that is driving the dissolution process and make \(ΔG_{soln}\) less negative and hence less spontaneous.
Determine the solubility of \(\ce{N2(g)}\) when combined with \(\ce{H2O}\) at 0.0345 °C the pressure of \(\ce{N2}\) is 1.00 atm, and its solubility is 21.0 ml at STP.
Solution
Begin by determining the molarity (solubility) of \(\ce{N2(g)}\) at 0 °C and STP.
At STP 1 mol=22L
\[\begin{align*} \text{Molarity of } \ce{N2} &= 21\,ml \left( \dfrac{1L}{1000\,ml}\right) \\[4pt] &=0.021\,L \,\ce{N2} \\[4pt] &= 0.021\,L \,\ce{N2} \left(\dfrac{1\,mol}{22\,L}\right)\\[4pt] &=\dfrac{0 .000954\,mol}{1\, L} \\[4pt] &= 9.5 \times 10^{-4}\, M\, \ce{N2} \end{align*}\]
Now that the molarity of \(\ce{N2}\). \(C\) has been attained, the Henry's law constant, \(k\), can be evaluated.
\[C = k_H P_{gas} \nonumber\]
where \(C\) is solubility, \(k_H\) is Henry's constant, and \(P_{gas}\) is the partial pressure of the gas being considered.
Rearranging the formula to solve for \(k_H\)
\[\begin{align} k_H&= \dfrac{C}{P_{gas}} \\ &= 9.5 \times 10^{-4}\, M \,N_2/ 1\,atm \nonumber \end{align} \nonumber\]
Now substitute k and the partial pressure of \(\ce{N2}\) into Henry's law:
\[\begin{align} C&= (9.5 \times 10^{-4}\,M\, N_2)(0.0345) \nonumber \\[4pt] &= 3.29 \times 10^{-5}\, M\, N_2 \nonumber \end{align} \nonumber\]
A fish kill can occur with rapid fluctuations in temperature or sustained high temperatures. Generally, cooler water has the potential to hold more oxygen, so a period of sustained high temperatures can lead to decreased dissolved oxygen in a body of water. A short period of hot weather can increase temperatures in the surface layer of water, as the warmer water tends to stay near the surface and be further heated by the air. In this case, the top warmer layer may have more oxygen than the lower, cooler layers because it has constant access to atmospheric oxygen.

Solubility of Gases in Organic Solvents
Dissolving gases in non-polar organic solvents is a different situation than in polar solvents like water discussed above. For non-polar solvents, both the solvent-solvent interactions (\(\Delta H_{\text{solvent-solvent}}\)) and the solvation enthalpies (\(\Delta H_{\text{solute-solvent}}\)) are considerably weaker than in polar liquids like water due to the absence of strong dipole-dipole intermolecular interactions (or hydrogen bonding). In many cases, the enthalpy needed to break solvent-solvent interactions is comparable to the enthalpy released in making solvent-gas interactions.
\[\Delta H_{\text{solvent-solvent}} \approx \Delta H_{\text{solute-solvent}}\]
which means the \(\Delta H_{sol} \approx 0\) via Equation \ref{eq2}. In some solvent-solute combination
\[\Delta H_{\text{solvent-solvent}} > \Delta H_{\text{solute-solvent}}\]
so that \(\Delta H_{sol} > 0\). In this case, we can write the solution reactions thusly
\[ \Delta + \ce{ solute (gas) + solvent (solvent) \rightleftharpoons solute (sol) + solvent (sol)} \label{eq5}\]
where \(Delta\) is thermal energy. In these cases, gases dissolved in organic solvents can actually be more soluble at higher temperatures. A Le Chatelier perspective, like that used above for water, can help understand why. Increasing the temperature will shift in the equilibrium to favor dissolution (i.e, shift Equation \ref{eq5} to the right). As a result, the solubilities of gases in organic solvents often increase with increasing temperature (Table \(\PageIndex{1}\)) in contrast to the trend observed in water (Figure \(\PageIndex{1}\)).
| Temperature (ºC) | \(\ce{H2}\) in n-hexane | \(\ce{H2}\) in Toluene | \(\ce{H2}\) in Acetonitrile | \(\ce{O_2}\) in Water | \(\ce{O_2}\) in Ethanol | \(\ce{O_2}\) in Decane |
|---|---|---|---|---|---|---|
| 25 | \(7.13 \times 10^4\) | \(3.15 \times 10^4\) | \(1.78 \times 10^4\) | \(0.249 \times 10^4\) | \(5.59 \times 10^4\) | \(21.78\times 10^4\) |
| 50 | \(8.20 \times 10^4\) | \(3.75 \times 10^4\) | \(2.16 \times 10^4\) | \(0.196 \times 10^4\) | \( 5.598 \times 10^4\) | \(21.76\times 10^4\) |
| 100 | \(10.78 \times 10^4\) | \(5.05 \times 10^4\) | \(3.02 \times 10^4\) | \(0.086 \times 10^4\) | \(5.695 \times 10^4\) | - |
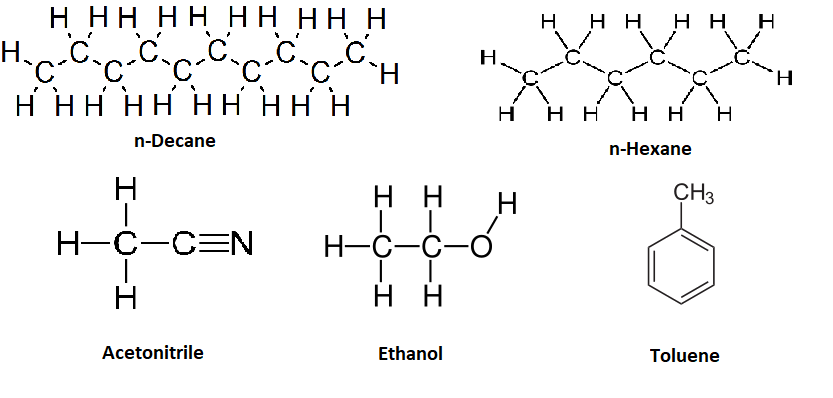
Based off of the three steps outlined above for dissolving a solute a liquid, explain why the solubility of hydrogen is smaller in acetonitrile than in toluene and that is less than in n-hexane.
- Answer
-
Acetinitrile is a polar organic solvent and has stronger intermolecular bonds than toluene, which is a weakly polar solvent and has stronger intermolecular interactions than n-hexane.
A system of cyclopentane and oxygen gas are at equilibrium with an enthalpy of -1234 kJ; predict whether the solubility of oxygen gas will be greater when heat is added to the system or when a temperature decrease occurs.
- Answer
-
Cyclopentane is an organic solvent. Oxygen gas and cyclopentane in a system at equilibrium, where the entropy is negative, will be be displaced from equilibrium when any type of temperature change is inflicted on the system. Because the dissolution of the gas is endothermic, more heat increases the solubility of the gas.
References
- Petrucci, et al. General Chemistry Principles & Modern Applications. 9th ed. Upper Saddle River, NJ: Pearson Prentice Hall, 2007
- Garde,Shekhar, Garcia, Angel, Pratt, Lawrence, Hummer, Gerhard. "Temperature Dependence of the Non-polar Solubility of Gases in Water". Biophysical Chemistry. Volume 78. Issues 1-2. 1999.


