Chromatography
- Page ID
- 55254
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Chromatography is a method by which a mixture is separated by distributing its components between two phases. The stationary phase remains fixed in place while the mobile phase carries the components of the mixture through the medium being used. The stationary phase acts as a constraint on many of the components in a mixture, slowing them down to move slower than the mobile phase. The movement of the components in the mobile phase is controlled by the significance of their interactions with the mobile and/or stationary phases. Because of the differences in factors such as the solubility of certain components in the mobile phase and the strength of their affinities for the stationary phase, some components will move faster than others, thus facilitating the separation of the components within that mixture.
Theory
The distribution of a solute between the mobile and stationary phases in chromatography is described by \(\kappa\), the partition coefficient, defined by:
\[\kappa = \dfrac{C_s }{C_m} \nonumber \]
where \(C_s\) is the concentration of solute in the stationary phase and \(C_m\) is the concentration of the solute in the mobile phase. The mobile phase serves to carry the sample molecules through the chromatographic column. During the sample molecules transportation through the column, each analyte is retained according to that compound's characteristic affinity for the stationary phase. The time that passes between the sample injection and peak maximum is called the retention time. The area underneath each peak is proportional to the amount of co responding analyte in solution.
Retention Time
The retention time, \(t_R\), is given in seconds by:
\[t_R = t_S + t_M \nonumber \]
where \(t_S\) is the time the analyte spends in the stationary phase and \(t_M\) is the time spent in the mobile phase. \(t_M\) is often referred to as the dead, or void time, as all components spend \(t_M\) in the mobile phase.
Theory of Band Broadening and Column Efficiency
Column efficiency is affected by the amount of band broadening that occurs as the sample passes through the column. Rate theory describes the shapes of the peaks in quantitative terms and is based upon the infinite number of paths that the sample may take in order to elute out of the column. Some molecules will travel through the column quickly due to their accidentally inclusion in the mobile phase while other molecules will severely lag behind because of their accidental inclusion in the stationary phase. The result of these effects is a typical Gaussian shaped chromatographic band with a spread of velocities around the mean value. Furthermore, the width of the peak increases as it move down the column because of the increased opportunity for spreading.
Two additional, undesirable chromatographic features are fronting and tailing. With fronting, the front of the peak is drawn out and the tali is steepened. The opposite is true for tailing. Both effects can be cause by distribution constant that varies with the concentration. These non-ideal effects are unwanted because of they lead to poor separations.
The two terms used to measure column efficiency are plate height, \(H\), and plate count, \(N\). These two terms related by the following equation where \(L\) is the length of the column:
\[ N = L / H \nonumber \]
Greater column efficiency is characterized by a large plate count \(N\) and a small plate height \(H\). Both \(H\) and \(N\) can be determined experimentally using the following two equations:
\[H = L W^2 / 16 (t_R)^2 \nonumber \]
\[N = 16 (t_R / W)^2 \nonumber \]
where L is the length of the column packing, W is the width of the magnitude of the base of the triangle and \(t_R\) is the retention time of the analyte. Using the theory of band broadening, the efficiency of chromatographic columns can be approximated by the van Deemter equation:
\[H = A + \dfrac{B}{u} + C_Su + C_Mu \nonumber \]
where \(H\) is the plate height in centimeters and u is the linear velocity of the mobile phase in centimeters per second. The term \(A\) describes the multiple path effect, or eddy diffusion, \(B\) describes the longitudinal diffusion coefficient and \(C_Su\) and \(C_Mu\) are the mass-transfer coefficients for the stationary and mobile phases, respectively.
The van Deemter Equation
In chromatography, it is important that the components in solution are adequately separated so that the separate components can be collected in their purest form. This becomes easier to do as the separation between the bands for each component have a greater separation between them. Also, it is ideal to have the bands of the individual components as narrow as possible. This is to say that it is best to have each component occupying as little space as possible within the column:
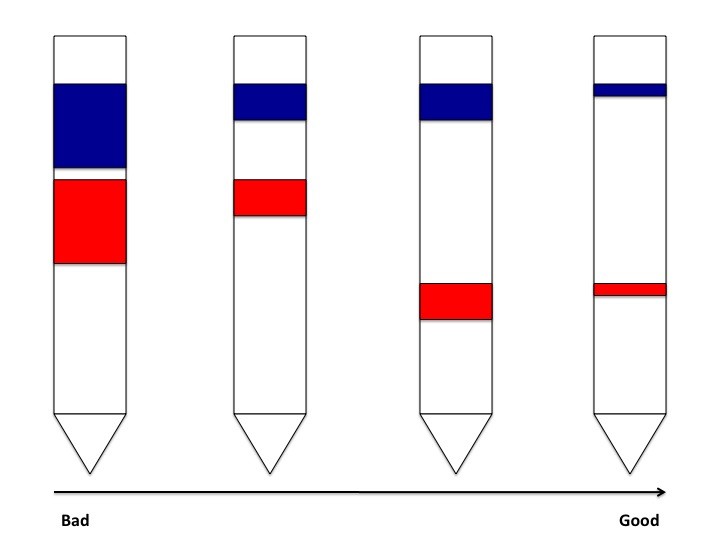
From this figure it can be seen that a better separation between narrow bands of components is ideal for easier collection of the individual samples. Band broadening is an especially important factor for this type of chromatography when separating colored compounds. When the bands of the components are narrow, most of the particles of that component are in close proximity with one another, which makes it easier to see the color of the bands. As the particles diffuse away from one another and broaden the component's band, the color of the band fades and can become more difficult to see, which may also make it harder to collect pure samples of the mixture's components.
The extent of band broadening in chromatography is determined by the Van Deemter equation3. This equation relates the efficiency of the chromatography procedure to three different factors. The Van Deemter equation is shown below:
\[H = Au^{1/3} + \dfrac{B}{u} + Cu \nonumber \]
Where H is the height equivalent of a theoretical plate4 (HETP) and u is the velocity (flow rate) of the mobile phase. The lower the resulting value of \(H\) is, the greater the efficiency of the procedure. So, ideally, a scientist will want to minimize all three terms in order to minimize \(H\). The other three terms refer to factors that come into play while the chromatography is performed.
The A factor is determined by a phenomenon called Eddy Diffusion5. This is also called the multi-path term, as molecular particles of a certain compound have a multitude of options when it comes to finding a pathway through a packed column. The following figure helps in visualizing Eddy diffusion:
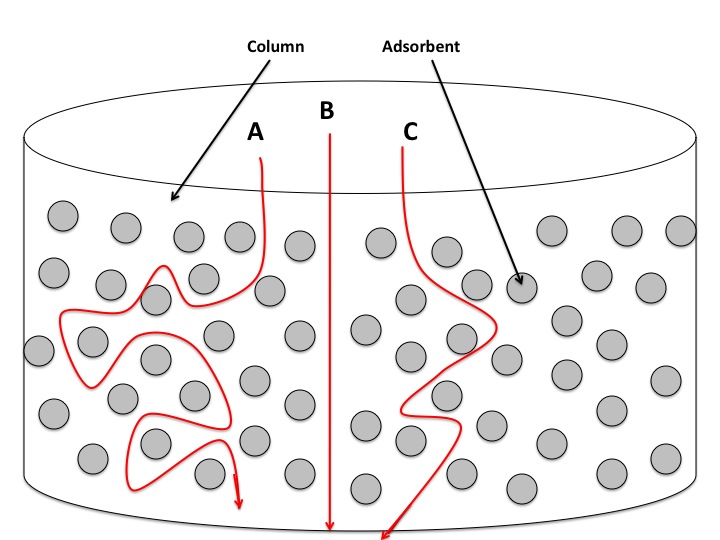
Because there is an almost infinite number of different paths that a particle can travel by through a column, some paths will be longer than others. The particles that find the shortest path through the column will be eluted more quickly than those that travel a longer way. In the figure, particle \(B\) will be eluted before particle \(C\), and both will be eluted before particle A. Since it is improbable for all particles of one compound to find the shortest path, there will be fractions of the component that will behave like particles \(A\), \(B\), and \(C\). This leads to the broadening of the band. There is little a scientist can do to minimize the Eddy Diffusion factor, as it is influenced by the nature of column being used and by the particles' movement through that column. The A term is loosely affected by the flow rate of the mobile phase, and sometimes the affect of the flow rate is negligible. It is for this reason that sometimes the Van Deemter equation is written as such:
\[H = A + \dfrac{B}{u} + Cu \nonumber \]
B/u is called the longitudinal diffusion term, and is caused by the components' natural migration from a place of high concentration (the center of the band) to a place of lower concentration (either side of the band) within the column. Diffusion6 occurs because molecules in a place of high concentration will tend to spread out to areas of lower concentration to achieve equilibrium. Given enough time, diffusion will result in equilibrium of the diffusing fluid via random molecular motion. The figure below helps to visualize this phenomenon:
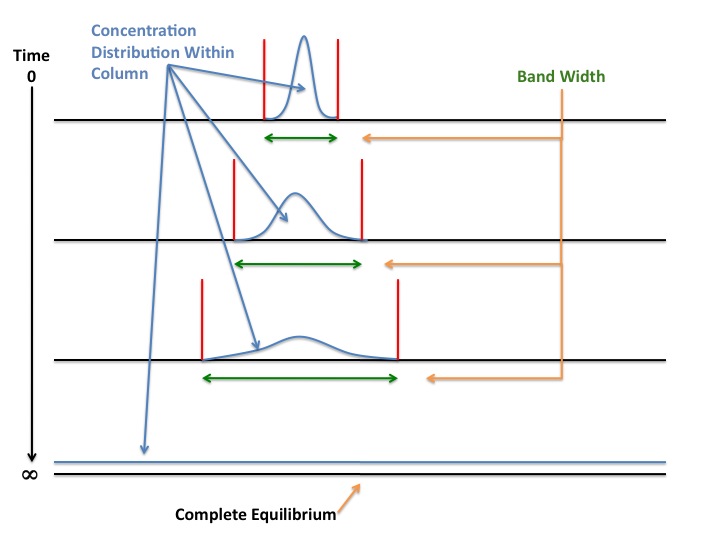
At time zero in the figure above, the particles of a compound are generally localized in a narrow band within the separating column. If the mobile phase flow rate is too small or if the system is left at rest, the particles begin to separate from one another. This causes a spread in the concentration distribution of that compound within the column, thus bringing about band broadening for the band of that particular compound. As the time that the system is left still approaches infinity, the compound reaches complete concentration equilibrium throughout the entire column. At this point, there is no definitive band for that component, as a single concentration of that compound is present throughout the entire column. Longitudinal diffusion is a chief cause of band broadening in Gas Chromatography, as the diffusion rates of gaseous species are much higher than those of liquids. It is for this reason that longitudinal diffusion is less of an issue in liquid chromatography. The magnitude of the term \(B/u\) can be minimized by increasing the flow rate of the mobile phase. Increasing the velocity of the mobile phase does not allow the components in the column to reach equilibrium, and so will hamper longitudinal diffusion. The flow rate of the mobile phase should not be increased in excess, however, as the term \(Cu\) is maximized when u is increased.
Cu is referred to as the mass transfer term. Mass transfer refers to when particles are so strongly adhered to the stationary phase that the mobile phase passes over them without carrying them along. This results is particles of a component being left behind. Since it is likely that more than a single particle of any given compound will undergo this occurrence, band broadening results. This results in a phenomenon called tailing, in which a fraction a component lags behind a more concentrated frontal band. Non-equilibrium effects can be caused by two phenomena: laminar flow and turbulent flow. Laminar flow7 occurs in tubular capillaries, and so is most prominent in Capillary Electrophoresis. Turbulent flow occurs as a result of particles becoming overwhelmed by the stationary phase and is more common in column chromatography. This occurrence can be visualized by observing the figure below:
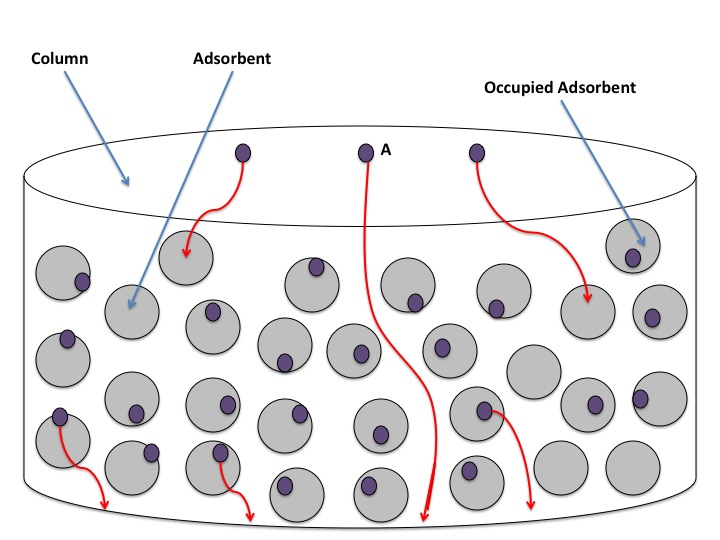
In the above figure, particles of the adsorbent solid become occupied by particles of the sample. If too many particles of the adsorbent are occupied, particle A will have nothing hindering it from flowing through the column. So, the particles of a single compound separate from one another. Also, as the mobile phase moves through the column, particles of the sample leave the stationary phase and migrate with the mobile phase. However, if the flow rate of the mobile phase is too high, many of the sample particles are unable to leave the stationary phase and so get left behind. These occurrences result in band broadening, as the individual particles of a single compound become less closely packed. The high flow rate of the mobile phase makes it more difficult for the components within the column to reach equilibrium between the stationary and mobile phase. It is for this reason that the Cu term is also called the non-equilibrium factor. Minimization of this factor can be achieved by decreasing the flow rate of the mobile phase. Decreasing the flow rate of the mobile phase gives sample components more time to leave the stationary phase and move with the mobile phase, thus reaching equilibrium.
By observing the Van Deemter equation, it can be deduced that an ideal mobile phase flow rate must be determined to yield the best (lowest) value of H. Decreasing the flow rate too much will result in an increase of the longitudinal diffusion factor B/u, while exceedingly increasing the flow rate will increase the significance of the mass transfer term Cu. So, H can be minimized to a finite limit depending on the various parameters involved in the chromatography being performed.

