Concentration Cell
- Page ID
- 290
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A concentration cell is an electrolytic cell that is comprised of two half-cells with the same electrodes, but differing in concentrations. A concentration cell acts to dilute the more concentrated solution and concentrate the more dilute solution, creating a voltage as the cell reaches an equilibrium. This is achieved by transferring the electrons from the cell with the lower concentration to the cell with the higher concentration.
Introduction
The standard electrode potential, commonly written as Eocell, of a concentration cell is equal to zero because the electrodes are identical. But, because the ion concentrations are different, there is a potential difference between the two half-cells. One can find this potential difference via the Nernst Equation,
\[ E_{cell} = E^\circ_{cell} - \dfrac{0.0592}{n}\log Q \]
at 25oC. The E stands for the voltage that can be measured using a voltmeter (make sure if the voltmeter measures it in millivolts that you convert the number before using it in the equation). Note that the Nernst Equation indicates that cell potential is dependent on concentration, which results directly from the dependence of free energy on concentration. Remember that to find Q you use this equation:
\[ \ce{$aA$ + $bB$ <=> $cC$ + $dD$} \]
\[ Q = \frac{[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}} \]
When Q=1, meaning that the concentrations for the products and reactants are the same, then taking the log of this equals zero. When this occurs, the Ecell is equal to the Eocell.
Another way to use the Eocell , or to find it, is using the equation below.
\[ E^\circ_{cell} = E^\circ_{cathode} - E^\circ_{anode}\]
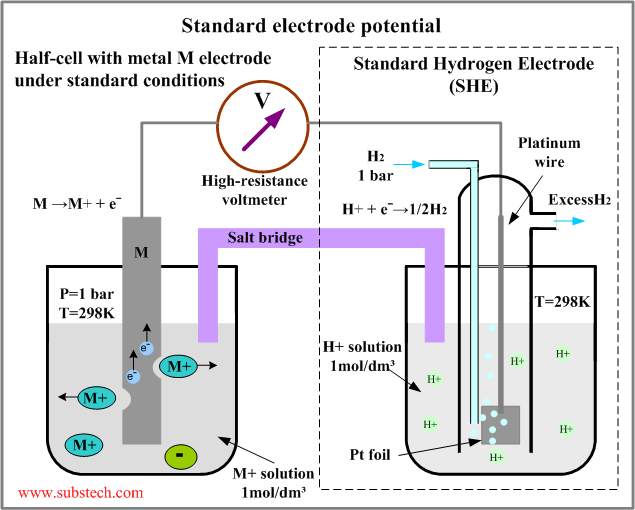
Fig.1 An example of a concentration cell
Connected Information
These concepts are useful for understanding the electron transfer and what occurs in half-cells.
Use of a Salt Bridge
The two compartments of a cell must be separated so they do not mix, but cannot be completely separated with no way for ions to be transferred. A wire cannot be used to connect the two compartments because it would react with the ions that flow from one side to another. Because of this, a salt bridge is an important part of a concentration cell. It solves the major problem of electrons beginning to pile up too much in the right beaker. This buildup is due to electrons moving from the left side, or left beaker, to the right side, or right beaker. The salt bridge itself can be in a few different forms, such as a salt solution in a U-tube or a porous barrier (direct contact). It evens the charge by moving ions to the left side, or left beaker. In the written expression which shows what is occurring in specific reactions, the salt bridge is represented by the double lines. An example of this would be:
\[ \text{Zn(s)} | \text{Zn}^{2+} (1~\text{M}) || \text{Cu}^{2+} (1~\text{M}) | \text{Cu} \]
The double lines between the Zn2+(1 M) and the Cu2+(1 M) signify the salt bridge. The single lines, however, do not represent bridges; they represent the different phase changes, for example, from solid zinc to liquid zinc solution. If there is a comma where you would expect to see a single line, this is not incorrect. It simply means that no phase changes occurred.
Electrode Use
In this type of reaction, there are two electrodes which are involved. These are known as the anode and the cathode, or the left and right side, respectively. The anode is the side which is losing electrons (oxidation) while the cathode is the side which is gaining electrons (reduction).
Use of a Voltmeter
A voltmeter (not to be confused with a different kind of voltmeter which also measures a type of energy) is used to measure the cell potential that is passed between the two sides. It is typically located in between the two cells. This cell potential (also known as an electromotive force) occurs due to the flow of electrons. The value it shows can be negative or positive depending on the direction in which the electrons are flowing. If the potential is positive then the transfer of electrons is spontaneous, but the reverse reaction is NONspontaneous. Conversely, if the value of the potential is negative, the transfer of electrons is nonspontaneous and the reverse reaction. The voltmeter measures this potential in volts or millivolts.
Electrons
The tendency of electrons to flow from one chemical to another is known as electrochemistry. This is what occurs in a concentration cell. The electrons flow from the left side (or left beaker) to the right side (or right beaker). Because the left side is losing electrons and the right is gaining them, the left side is called the oxidation side and the right side is the reduction side. Although you could switch the two to be on the opposite sides, this is the general way in which the set up is done. The oxidation side is called the anode and the reduction side is the cathode. It is the flow of the electrons that cause one side to be oxidized and the other to be reduced.
Corrosion
Corrosion can occur on a concentration cell when the metal being used is in contact with different concentrations, causing parts of the metal to have different electric potential than the other parts. One element that is often linked to this corrosion is oxygen. In the areas in which there is a low oxygen concentration corrosion occurs.
This can be somewhat prevented through sealing off the cell and keeping it clean, but even this cannot prevent any corrosion from occurring at some point.
Corrosion is most frequently a problem when the cell is in contact with soil. Because of the variations that occur within soil, which is much greater than the variations that occur within a fluid, contact with soil often causes corrosion for the cell.
Uses of Concentration Cells
A pH meter is a specific type of concentration cell that uses the basic setup of a concentration cell to determine the pH, or the acidity/basicity, of a specific solution. It is comprised of two electrodes and a voltmeter. One of the electrodes, the glass one has two components: a metal (commonly silver chloride) wire and a separate semi-porous glass part filled with a potassium chloride solution with a pH of 7 surrounding the AgCl. The other electrode is called the reference electrode, which contains a potassium chloride solution surrounding a potassium chloride wire. The purpose of this second electrode is to act as a comparison for the solution being tested. When the glass electrode comes into contact with a solution of different pH, an electric potential is created due to the reaction of the hydrogen ions with the metal ions. This potential is then measured by the voltmeter, which is connected to the electrode. The higher the voltage, the more hydrogen ions the solution contains, which means the solution is more acidic.
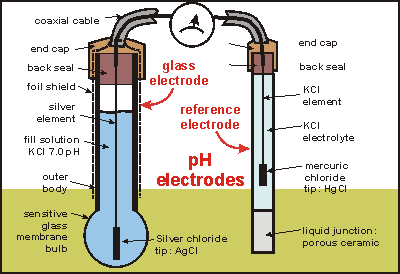
Fig.2 An example of a pH meter
Outside links
- http://en.Wikipedia.org/wiki/Concentration_cell
- Ciparick, Joseph D. "Half cell reactions: Do students ever see them? (TD)." J. Chem. Educ. 1991, 68, 247.
- Tanis, David O. "Galvanic cells and the standard reduction potential table (F&R)." J. Chem. Educ. 1990, 67, 602.
References
- Petrucci, Ralph H. General Chemistry: Principles and Modern Applications 9th Ed. New Jersey: Pearson Education Inc. 2007.
- Zumdahl, steven S. Chemistry, 9th Ed. New York: Houghton Mifflin Co. 2007.
Problems
1.) For the concentration cell bellow determine the flow of electrons.
\[ \text{Fe} | \text{Fe}^{2+}(0.01~\text{M}) || \text{Fe}^{2+}(0.1~\text{M})| \text{Fe}\]
Solution:
The cells will reach equilibrium if electrons are transferred from the left side to the right side. As a result, Fe2+ will be formed in the left compartment and metal iron will be deposited on the right electrode.
2.) Calculate cell potential for a concentration cell with two silver electrodes with concentrations 0.2 M and 3.0 M.
Solution:
Reaction:
\[ \ce{Ag^{2+} + 2e^- -> Ag(s)}\]
Cell Diagram:
\[ \text{Ag(s)}|\text{Ag}^{2+}(0.2~\text{M})||\text{Ag}^{2+}(3.0~\text{M})|\text{Ag(s)}\]
Nernst Equation:
\[ E = E^\circ - \dfrac{0.0592}{2}\log \dfrac{0.02}{3.0}\]
**Eo= 0 for concentration cells
E = 0.0644 V
3.) Calculate the concentration of the unknown, given the equation below and a cell potential of 0.26&nsbp;V.
\[ \text{Ag}|\text{Ag}^+(x~\text{M})||\text{Ag}^+(1.0~\text{M})|\text{Ag} \]
\[ E = E^\circ - \dfrac{0.0592}{1} \log \dfrac{x}{1.0}\]
\[0.26 = 0 - 0.0592 \log \dfrac{x}{1.0}\]
\[4.362 = -\log(x) + \log(1.0)\]
\[\log(x) = \log(1.0) - 4.362\]
x = 4.341 x 10-5 M
Contributors and Attributions
- SSReno, Rainna Lim