Voltaic Cells

In redox reactions, electrons are transferred from one species to another. If the reaction is spontaneous, energy is released, which can then be used to do useful work. To harness this energy, the reaction must be split into two separate half reactions: the oxidation and reduction reactions. The reactions are put into two different containers and a wire is used to drive the electrons from one side to the other. In doing so, a Voltaic/ Galvanic Cell is created.

Introduction

When a redox reaction takes place, electrons are transferred from one species to the other. If the reaction is spontaneous, energy is released, which can be used to do work. Consider the reaction of a solid copper (Cu_(s)) in a silver nitrate solution (AgNO_3(s)).

\[2Ag^+_{(aq)} + Cu_{(s)} \leftrightharpoons Cu^{2+}_{(aq)} + 2Ag_{(s)} \nonumber \]

The \(AgNO_{3\;(s)}\) dissociates in water to produce \(Ag^+_{(aq)}\) ions and \(NO­­^-_{3\;(aq)}\) ions. The NO₃^-_(aq) ions can be ignored since they are spectator ions and do not participate in the reaction. In this reaction, a copper electrode is placed into a solution containing silver ions. The Ag⁺_(aq) will readily oxidize Cu_(s) resulting in Cu²⁺_(aq), while reducing itself to Ag_(s).

This reaction releases energy. When the copper electrode solid is placed directly into a silver nitrate solution, however, the energy is lost as heat and cannot be used to do work. In order to harness this energy and use it do useful work, we must split the reaction into two separate half reactions; The oxidation and reduction reactions. A wire connects the two reactions and allows electrons to flow from one side to the other. In doing so, we have created a Voltaic/ Galvanic Cell.

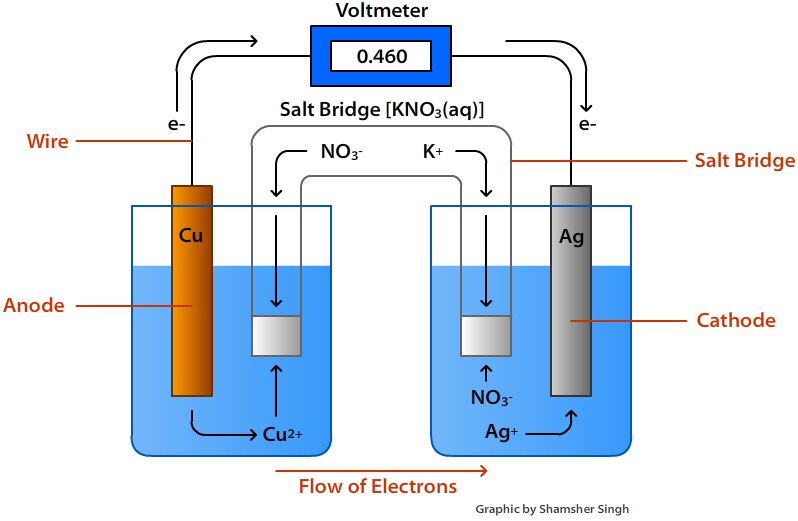
Figure \(\PageIndex{1}\): Voltaic Cell

A Voltaic Cell (also known as a Galvanic Cell) is an electrochemical cell that uses spontaneous redox reactions to generate electricity. It consists of two separate half-cells. A half-cell is composed of an electrode (a strip of metal, M) within a solution containing Mⁿ⁺ ions in which M is any arbitrary metal. The two half cells are linked together by a wire running from one electrode to the other. A salt bridge also connects to the half cells. The functions of these parts are discussed below.

Half Cells

Half of the redox reaction occurs at each half cell. Therefore, we can say that in each half-cell a half-reaction is taking place. When the two halves are linked together with a wire and a salt bridge, an electrochemical cell is created.

Electrodes

An electrode is strip of metal on which the reaction takes place. In a voltaic cell, the oxidation and reduction of metals occurs at the electrodes. There are two electrodes in a voltaic cell, one in each half-cell. The cathode is where reduction takes place and oxidation takes place at the anode.

Through electrochemistry, these reactions are reacting upon metal surfaces, or electrodes. An oxidation-reduction equilibrium is established between the metal and the substances in solution. When electrodes are immersed in a solution containing ions of the same metal, it is called a half-cell. Electrolytes are ions in solution, usually fluid, that conducts electricity through ionic conduction. Two possible interactions can occur between the metal atoms on the electrode and the ion solutions.

1. Metal ion Mⁿ⁺ from the solution may collide with the electrode, gaining "n" electrons from it, and convert to metal atoms. This means that the ions are reduced.
2. Metal atom on the surface may lose "n" electrons to the electrode and enter the solution as the ion Mⁿ⁺ meaning that the metal atoms are oxidized.

When an electrode is oxidized in a solution, it is called an anode and when an electrode is reduced in solution. it is called a cathode.

• Anode: The anode is where the oxidation reaction takes place. In other words, this is where the metal loses electrons. In the reaction above, the anode is the Cu(s) since it increases in oxidation state from 0 to +2.
• Cathode: The cathode is where the reduction reaction takes place. This is where the metal electrode gains electrons. Referring back to the equation above, the cathode is the Ag(s) as it decreases in oxidation state from +1 to 0.

Remembering Oxidation and Reduction

When it comes to redox reactions, it is important to understand what it means for a metal to be “oxidized” or “reduced”. An easy way to do this is to remember the phrase “OIL RIG”.

OIL = Oxidization is Loss (of e^-)

RIG = Reduction is Gain (of e^-)

In the case of the example above \(Ag^+_{(aq)}\) gains an electron meaning it is reduced. \(Cu_{(s)}\) loses two electrons thus it is oxidized.

The salt bridge is a vital component of any voltaic cell. It is a tube filled with an electrolyte solution such as KNO_3(s) or KCl_(s). The purpose of the salt bridge is to keep the solutions electrically neutral and allow the free flow of ions from one cell to another. Without the salt bridge, positive and negative charges will build up around the electrodes causing the reaction to stop.

The purpose of the salt bridge is to keep the solutions electrically neutral and allow the free flow of ions from one cell to another.

Flow of Electrons

Electrons always flow from the anode to the cathode or from the oxidation half cell to the reduction half cell. In terms of E^ocell of the half reactions, the electrons will flow from the more negative half reaction to the more positive half reaction. A cell diagram is a representation of an electrochemical cell. The figure below illustrates a cell diagram for the voltaic shown in Figure \(\PageIndex{1}\) above.

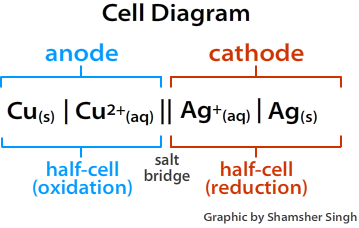
Figure \(\PageIndex{2}\): Cell Diagram. The figure below illustrates a cell diagram for the voltaic shown in Figure \(\PageIndex{1}\).

When drawing a cell diagram, we follow the following conventions. The anode is always placed on the left side, and the cathode is placed on the right side. The salt bridge is represented by double vertical lines (||). The difference in the phase of an element is represented by a single vertical line (|), while changes in oxidation states are represented by commas (,).

When asked to construct a cell diagram follow these simple instructions. Consider the following reaction:

\[2Ag^+_{(aq)} + Cu_{(s)} \rightleftharpoons Cu^{2+}_{(aq)} + 2Ag_{(s)} \nonumber \]

Step 1: Write the two half-reactions.

\[Ag^+_{(aq)} + e^- \rightleftharpoons Ag_{(s)} \nonumber \]

\[Cu_{(s)} \rightleftharpoons Cu^{2+}_{(aq)} + 2e^- \nonumber \]

Step 2: Identify the cathode and anode.

\(Cu_{(s)}\) is losing electrons thus being oxidized; oxidation occurs at the anode.

• Anode (where oxidation occurs): \(Cu_{(s)} \rightleftharpoons Cu^{2+}_{(aq)} + 2e^-\)

\(Ag^+\) is gaining electrons thus is being reduced; reduction happens at the cathode.

• Cathode (where reduction occurs): \(Ag^+_{(aq)} + e^- \rightleftharpoons Ag_{(s)}\)

Step 3: Construct the Cell Diagram.

\[Cu_{(s)} | Cu^{2+}_{(aq)} || Ag^+_{(aq)} | Ag_{(s)} \nonumber \]

The anode always goes on the left and cathode on the right. Separate changes in phase by | and indicate the the salt bridge with ||. The lack of concentrations indicates solutions are under standard conditions (i.e., 1 M)

Example \(\PageIndex{1}\)

Consider the following two reactions:

\[Cu^{2+}_{(aq)} + Ba_{(s)} \rightarrow Cu_{(s)} + Ba^{2+}_{(aq)} \nonumber \]

\[2Al_{(s)} + 3Sn^{2+}_{(aq)} \rightarrow 2Al^{3+}_{(aq)} + 3Sn_{(s)} \nonumber \]

1. Split the reaction into half reactions and determine their standard reduction potentials. Indicate which would be the anode and cathode.
2. Construct a cell diagram for the following each reactions.
3. Determine the \(E^o_{cell}\) for the voltaic cell formed by each reaction.

Solution

1.a) Ba²⁺_(aq) → Ba_(s) + 2e- with SRP (for opposite reaction) E^o = -2.92 V (Anode; where oxidation happens)

Cu_²⁺(aq) + 2e- → Cu_(s) with SRP E^o = +0.340 V (Cathode; where reduction happens)

1.b) Al³⁺_(aq) → Al_(s) + 3e^- with SRP (for opposite reaction) E^o = -1.66 V (Anode; where oxidation happens)

Sn²⁺_(aq) +2e^- → Sn_(s) with SRP E^o = -0.137 V (Cathode; where reduction happens)

2.a) Ba²⁺_(aq) | Ba_(s) || Cu_(s) | Cu_²⁺(aq)

2.b) Al_(s) | Al³⁺_(aq) || Sn²⁺_(aq) | Sn_(s)

3.a) E^o_cell = 0.34 - (-2.92) = 3.26 V

3.b) E^o_cell = -0.137 - (-1.66) = 1.523 V

Cell Voltage/Cell Potential

The readings from the voltmeter give the reaction's cell voltage or potential difference between it's two two half-cells. Cell voltage is also known as cell potential or electromotive force (emf) and it is shown as the symbol \(E_{cell}\).

Standard Cell Potential:

\[E^o_{cell} = E^o_{cathode} - E^o_{anode} \nonumber \]

The E^o values are tabulated with all solutes at 1 M and all gases at 1 atm. These values are called standard reduction potentials. Each half-reaction has a different reduction potential, the difference of two reduction potentials gives the voltage of the electrochemical cell. If E^ocell is positive the reaction is spontaneous and it is a voltaic cell. If the E^ocell is negative, the reaction is non-spontaneous and it is referred to as an electrolytic cell.

References

1. Brady, James E., Holum, John R. “Chemistry: The Study of Matter and Its Changes”, John Wiley & Sons Inc 1993
2. Brown, Theodore L., LeMay, H. Eugene Jr. “Chemistry: The Central Science” Third Edition, Prentice-Hall, Inc. Englewood Cliffs, N.J. 07632 1985
3. Brown, Theodore L., LeMay, H. Eugene Jr., Bursten, Bruce E. “Chemistry: The Central Science” Fifth Edition, Prentice-Hall, Inc. Englewood Cliffs, N.J. 07632 1991
4. Gesser, Hyman D. “ Descriptive Principles of Chemistry”, C.V. Mosby Company 1974
5. Harwood, William, Herring, Geoffrey, Madura, Jeffry, and Petrucci, Ralph, General Chemistry: Principles and Modern Applications, Ninth Edition, Upper Saddle River,New Jersey, Pearson Prentice Hall, 2007.
6. Petrucci, Ralph H. Genereal Chemistry: Principles and Modern Applications 9th Ed. New Jersey: Pearson Education Inc. 2007.
7. Vassos Basil H. Electroanaytical Chemistry. New York: Wiley-Interscience Publication. 1983.
8. Zumdahl, Steven S. Chemistry 7th Ed. New York: Houghton Mifflin Company. 2007.

Contributors and Attributions

• Shamsher Singh, Deborah Gho