3.5: Ion Chromatography
- Page ID
- 55868
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ion Chromatography is a method of separating ions based on their distinct retention rates in a given solid phase packing material. Given different retention rates for two anions or two cations, the elution time of each ion will differ, allowing for detection and separation of one ion before the other. Detection methods are separated between electrochemical methods and spectroscopic methods. This guide will cover the principles of retention rates for anions and cations, as well as describing the various types of solid-state packing materials and eluents that can be used.
Principles of Ion Chromatography
Retention Models in Anion Chromatography
The retention model for anionic chromatography can be split into two distinct models, one for describing eluents with a single anion, and the other for describing eluents with complexing agents present. Given an eluent anion or an analyte anion, two phases are observed, the stationary phase (denoted by S) and the mobile phase (denoted by M). As such, there is equilibrium between the two phases for both the eluent anions and the analyte anions that can be described by Equation \ref{1}.
\[ y*[A^{x-}_{M}]\ +\ x*[E^{y-}_{S}]\ \Leftrightarrow \ y*[A^{x-}_{S}]\ +\ x*[E^{y-}_{M}] \label{1} \]
This yields an equilibrium constant as given in Equation \ref{2} .
\[ K_{A,E} = \frac{ [A^{x-}_{S}]^{y} [E^{y-}_{M}]^{x} \gamma ^{y} _{A^{x-}_{S} } \gamma ^{x} _{E^{y-}_{S}} }{ [A^{x-}_{M}] ^{y} [E^{y-}_{S}]^{x} \gamma ^{y} _{A^{x-}_{M}} \gamma ^{x} _{E^{y-}_{S}}} \label{2} \]
Given the activity of the two ions cannot be found in the stationary or mobile phases, the activity coefficients are set to 1. Two new quantities are then introduced. The first is the distribution coefficient, DA, which is the ratio of analyte concentrations in the stationary phase to the mobile phase, Equation \ref{3} . The second is the retention factor, k1A, which is the distribution coefficient times the ratio of volume between the two phases, Equation \ref{4} .
\[ D_{A} \ =\ \frac{[A_{S}]}{[A_{M}]} \label{3} \]
\[k_{A}^{1} \ = \ D_{A} * \frac{V_{S}}{V_{M}} \label{4} \]
Substituting the two quantities from Equation \ref{3} and Equation \ref{4} into Equation \ref{2} , the equilibrium constant can be written as Equation \ref{5}
\[ K_{A,E} \ = (k_{A}^{1} \frac{V_{M}}{V_{S}})^{y} * (\frac{[E_{M}^{y-} ]}{[E^{y-}_{S}]})^{x} \label{5} \]
Given there is usually a large difference in concentrations between the eluent and the analyte (with magnitudes of 10 greater eluent), equation 4 can be re-written under the assumption that all the solid phase packing material’s functional groups are taken up by Ey-. As such, the stationary Ey- can be substituted with the exchange capacity divided by the charge of Ey-. This yields Equation \ref{6}
\[ K_{A,E} \ = (k_{A}^{1} \frac{V_{M}}{V_{S}})^{y} * (\frac{Q}{\gamma })^{-x} [E_{M}^{y-}] \label{6} \]
Solving for the retention factor Equation \ref{7} is developed.
\[ z*[A^{x-}_{M}] \ +\ x*[B^{z-}_{S}] \Leftrightarrow z* [A^{x-}_{S}] \ +\ x*[B^{z-}_{M}] \label{7} \]
Equation \ref{8} shows the relationship between retention factor and parameters like eluent concentration and the exchange capacity, which allows parameters of the ion chromatography to be manipulated and the retention factors to be determined. Equation \ref{9} only works for a single analyte present, but a relationship for the selectivity between two analytes [A] and [B] can easily be determined.
First the equilibrium between the two analytes is determined as Equation \ref{8}
\[ K_{A,B} \ = \frac{[A^{x-}_{S}]^{z} [B^{z-}_{M}]^{x}}{[A^{x-}_{M}]^{z} [B^{z-}_{S}]^{x}} \label{8} \]
The equilibrium constant can be written as Equation \ref{9} (ignoring activity):
\[ \alpha _{A,B} \ = \frac{[A^{x-}_{S}][B^{z-}_{M}]}{[A^{x-}_{M}][B^{z-}_{S}]} \label{9} \]
The selectivity can then be determined to be Equation \ref{10}
\[ \alpha _{A,B} \ = \frac{[A^{x-}_{S}][B^{z-}_{M}]}{[A^{x-}_{M}][B^{z-}_{S}]} \label{10} \]
Equation \ref{10} can then be simplified into a logarithmic form as the following two equations:
\[ \log \alpha _{A,B} = \frac{1}{z} log K_{A,B} \ + \frac{x-z}{z} log \frac{ k_{A}^{1} V_{M}}{V_{S}} \label{11} \]
\[ \log \alpha _{A,B} = \frac{1}{x} log K_{A,B} \ + \frac{x-z}{z} log \frac{ k_{A}^{1} V_{M}}{V_{S}} \label{12} \]
When the two charges are the same, it can be seen that the selectivity is only a factor of the selectivity coefficients and the charges. When the two charges are different, it can be seen that the two retention factors are dependent upon each other.
In situations with a polyatomic eluent, three models are used to account for the multiple anions in the eluent. The first is the dominant equilibrium model, in which one anion is so dominant in concentration; the other eluent anions are ignored. The dominant equilibrium model works best for multivalence analytes. The second is the effective charge model, where an effective charge of the eluent anions is found, and a relationship similar to EQ is found with the effective charge. The effective charge models works best with monovalent analytes. The third is the multiple eluent species model, where Equation \ref{13} describes the retention factor:
\[ \log K_{A}^{1} \ =\ C_{3} - (\frac{X_{1}}{a} + \frac{X_{2}}{b} + \frac{X_{3}}{c}) -\ log C_{P} \label{13} \]
C3 is a constant that includes the phase volume ratio between stationary, the equilibrium constant, and mobile and the exchange capacity. Cp is the total concentration of the eluent species. X1, X2, X3, correspond to the shares of a particular eluent anion in the retention of the analyte.
Retention Models of Cation Chromatography
For eluents with a single cation and analytes that are alkaline earth metals, heavy metals or transition metals, a complexing agent is used to bind with the metal during chromatography. This introduces the quantity A(m) to the retention rate calculations, where A(m) is the ratio of free metal ion to the total concentration of metal. Following a similar derivation to the single anion case, Equation \ref{14} is found.
\[ K_{A,E} = \ (\frac{ k_{A}^{1}}{ \alpha _{M} \phi } )^{y} * (\frac{Q}{\gamma })^{-x} [E ^{y+} _{M} ]^{x} \label{14} \]
Solving for the retention coefficient, Equation \ref{15} is found.
\[ k_{A}^{1} = \alpha _{M} \phi * K_{A,E} ^{\frac{1}{\gamma } } (\frac{Q}{\gamma })^{\frac{x}{y} } ([E_{M}^{y+}]^{- \frac{x}{y} } \label{15} \]
From this expression, the retention rate of the cation can be determined from eluent concentration and the ratio of free metal ions to the total concentration of the metal, which itself is depended on the equilibrium of the metal ion with the complexing agent.
Solid Phase Packing Materials
The solid phase packing material used in the chromatography column is important to the exchange capacity of the anion or cation. There are many types of packing material, but all share a functional group that can bind either the anion or the cation complex. The functional group is mounted on a polymer surface or sphere, allowing large surface area for interaction.
Packing Material for Anion Chromatography
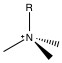
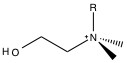
The primary functional group used for anion chromatography is the ammonium group. Amine groups are mounted on the polymer surface, and the pH is lowered to produce ammonium groups. As such, the exchange capacity is depended on the pH of the eluent. To reduce the pH dependency, the protons on the ammonium are successively replaced with alkyl groups until the all the protons are replaced and the functional group is still positively charged, but pH independent. The two packing materials used in almost all anion chromatography are trimethylamine (NMe3, Figure \(\PageIndex{1}\) ) and dimethylanolamine (Figure \(\PageIndex{2}\) ).
Packing Material for Cation Chromatography
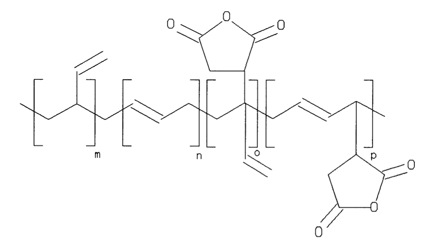
Cation chromatography allows for the use of both organic polymer based and silica gel based packing material. In the silica gel based packing material, the most common packing material is a polymer-coated silica gel. The silicate is coated in polymer, which is held together by cross-linking of the polymer. Polybutadiene maleic acid (Figure \(\PageIndex{3}\) ) is then used to create a weakly acidic material, allowing the analyte to diffuse through the polymer and exchange. Silica gel based packing material is limited by the pH dependent solubility of the silica gel and the pH dependent linking of the silica gel and the functionalized polymer. However, silica gel based packing material is suitable for separation of alkali metals and alkali earth metals.
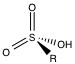
Organic polymer based packing material is not limited by pH like the silica gel materials are, but are not suitable for separation of alkali metals and alkali earth metals. The most common functional group is the sulfonic acid group (Figure \(\PageIndex{4}\) ) attached with a spacer between the polymer and the sulfonic acid group.
Detection Methods
Spectroscopic Detection Methods
Photometric detection in the UV region of the spectrum is a common method of detection in ion chromatography. Photometric methods limit the eluent possibilities, as the analyte must have a unique absorbance wavelength to be detectable. Cations that do not have a unique absorbance wavelength, i.e. the eluent and other contaminants have similar UV visible spectra can be complexed to for UV visible compounds. This allows detection of the cation without interference from eluents.
Coupling the chromatography with various types of spectroscopy such as Mass spectroscopy or IR spectroscopy can be a useful method of detection. Inductively coupled plasma atomic emission spectroscopy is a commonly used method.
Direct Conductivity Methods
Direct conductivity methods take advantage of the change in conductivity that an analyte produces in the eluent, which can be modeled by Equation \ref{16} where equivalent conductivity is defined as Equation \ref{17} .
\[ \Delta K \ =\frac{(\Lambda _{A} \ -\ \Lambda _{g} ) * C_{s}}{1000} \label{16} \]
\[ \Lambda \ =\frac{L}{A*R} * \frac{1}{C} \label{17} \]
With L being the distance between two electrodes of area A and R being the resistance the ion creates. C is the concentration of the ion. The conductivity can be plotted over time, and the peaks that appear represent different ions coming through the column as described by Equation \ref{18}
\[ K_{peak} \ =\ (\Lambda _{A} \ -\ \Lambda _{g})*C_{A} \label{18} \]
The values of Equivalent conductivity of the analyte and of the eluent common ions can be found in Table \(\PageIndex{1}\)
| Cations | \(\Lambda ^{+} (S\ cm^{2} eq^{-1} ) \) | Anions | \(\Lambda ^{-} (S\ cm^{2} eq^{-1} ) \) |
|---|---|---|---|
| \( H^{+} \) | 350 | \( OH^{-} \) | 198 |
| \( Li ^{+} \) | 39 | \( F^{-} \) | 54 |
| \( Na^{+} \) | 50 | \( Cl^{-} \) | 76 |
| \( K^{+} \) | 74 | \( Br^{-} \) | 78 |
| \( NH^{4+} \) | 73 | \( I^{-} \) | 77 |
| \( 1/2 Mg^{2+} \) | 53 | \( NO^{-}_{2} \) | 72 |
| \( 1/2 Ca^{2+} \) | 60 | \( NO^{-}_{3} \) | 71 |
| \( 1/2Sr^{2+} \) | 59 | \( HCO_{3}^{-} \) | 45 |
| \( 1/2 Ba^{2+} \) | 64 | \( 1/2 CO_{3}^{2-} \) | 72 |
| \( 1/2 Zn^{2+} \) | 52 | \( H_{2}PO_{4}^{-} \) | 33 |
| \( 1/2 Hg^{2+} \) | 53 | \( 1/2 HPO_{4}^{-} \) | 57 |
| \( 1/2 Cu^{2+} \) | 55 | \( 1/3 PO_{4}^{-} \) | 69 |
| \( 1/2 Pb ^{2+} \) | 71 | \( 1/2 SO_{4}^{2-} \) | 80 |
| \( 1/2 Co ^{2+} \) | 53 | \( CN^{-} \) | 82 |
| \( 1/3 Fe^{3+} \) | 70 | \( SCN^{-} \) | 66 |
| \( N(Et)^{4+} \) | 33 | Acetate | 41 |
| 1/2 Phthalate | 38 | ||
| Propionate | 36 | ||
| Benzoate | 32 | ||
| Salicylate | 30 | ||
| 1/2 Oxalate | 74 |
Eluents
The choice of eluent depends on many factors, namely, pH, buffer capacity, the concentration of the eluent, and the nature of the eluent’s reaction with the column and the packing material.
Eluents in Anion Chromatography
In non-suppressed anion chromatography, where the eluent and analyte are not altered between the column and the detector, there is a wide range of eluents to be used. In the non-suppressed case, the only issue that could arise is if the eluent impaired the detection ability (absorbing in a similar place in a UV-spectra as the analyte for instance). As such, there are a number of commonly used eluents. Aromatic carboxylic acids are used in conductivity detection because of their low self-conductivity. Aliphatic carboxylic acids are used for UV/visible detection because they are UV transparent. Inorganic acids can only be used in photometric detection.
In suppressed anion chromatography, where the eluent and analyte are treated between the column and detection, fewer eluents can be used. The suppressor modifies the eluent and the analyte, reducing the self-conductivity of the eluent and possibly increasing the self-conductivity of the analyte. Only alkali hydroxides and carbonates, borates, hydrogen carbonates, and amino acids can be used as eluents.
Eluents in Cation Chromatography
The primary eluents used in cation chromatography of alkali metals and ammoniums are mineral acids such as HNO3. When the cation is multivalent, organic bases such as ethylenediamine (Figure \(\PageIndex{5}\) ) serve as the main eluents. If both alkali metals and alkali earth metals are present, hydrochloric acid or 2,3-diaminopropionic acid (Figure \(\PageIndex{6}\) ) is used in combination with a pH variation. If the chromatography is unsuppressed, the direct conductivity measurement of the analyte will show up as a negative peak due to the high conductivity of the H+ in the eluent, but simple inversion of the data can be used to rectify this discrepancy.

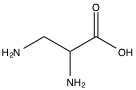
If transition metals or H+ are the analytes in question, complexing carboxylic acids are used to suppress the charge of the analyte and to create photometrically detectable complexes, forgoing the need for direct conductivity as the detection method.


