5: Raman Spectroscopy

Consider the molecular vibrations of carbon dioxide and determine whether or not they are Raman active.

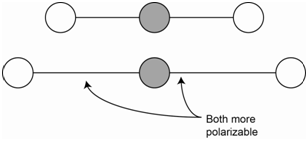
The symmetric stretch of carbon dioxide is not IR active because there is no change in the net molecular dipole (Figure \(\PageIndex{1}\)). Since both bonds are stretched (i.e., lengthened), both bonds are more easily polarizable. The overall molecular polarizability changes and the symmetric stretch is Raman active.

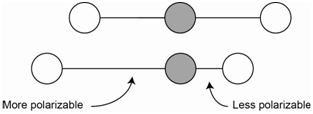
The asymmetric stretch of carbon dioxide is IR active because there is a change in the net molecular dipole (Figure \(\PageIndex{2}\)). In the asymmetric stretch, one bond is stretched and is now more polarizable while the other bond is compressed and is less polarizable. The change in polarizability of the longer bond is exactly offset by the change in the shorter bond such that the overall polarizability of the molecule does not change. Therefore, the asymmetric stretch is not Raman active.

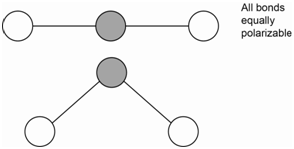
The bending motion of carbon dioxide is IR active because there is a change in the net molecular dipole (Figure \(\PageIndex{3}\)). Since the bending motion involves no changes in bond length, there is no change in the polarizability of the molecule. Therefore, the bending motion is not Raman active.

Note that the IR active vibrations of carbon dioxide (asymmetric stretch, bend) are Raman inactive and the IR inactive vibration (symmetric stretch) is Raman active. This does not occur with all molecules, but often times, the IR and Raman spectra provide complementary information about many of the vibrations of molecular species. Raman spectra are usually less complex than IR spectra.

An intriguing aspect of Raman spectroscopy is that information about the vibrational transitions is obtained using visible radiation. The process involves shining monochromatic visible radiation on the sample. The visible radiation interacts with the molecule and creates something that is known as a virtual state. From this virtual state it is possible to have a modulated scatter known as Raman scatter. Raman scatter occurs when there is a momentary distortion of the electrons in a bond of a molecule. The momentary distortion means that the molecule has an induced dipole and is temporarily polarized. As the bond returns to its normal state, the radiation is reemitted as Raman scatter.

One form of the modulated scatter produces Stokes lines. The other produces anti-Stokes lines. Stokes lines are scattered photons that are reduced in energy relative to the incident photons that interacted with the molecule. The reductions in energy of the scatter photons are proportional to the energies of the vibrational levels of the molecule. Anti-Stokes lines are scattered photons that are increased in energy relative to the incident photons that interacted with the molecule. The increases in energy of the scatter photons are proportional to the energies of the vibrational levels of the molecule.

The energy level diagram in Figure \(\PageIndex{4}\) shows representations for IR absorption, Rayleigh scatter, Stokes Raman scatter and anti-Stokes Raman scatter. For Stokes lines, the incident photons interact with a ground state molecule and form a virtual state. The scattered photons come from molecules that end up in excited vibrational states of the ground state, thereby explaining why they are lower in energy than the incident photons. For anti-Stokes lines, the incident photons interact with a molecule that is vibrationally excited. The virtual state produced by this interaction has more energy than the virtual state produced when the incident photon interacted with a ground state molecule. The scattered photons come from molecules that end up in the ground state, thereby explaining why they are higher in energy than the incident photons.

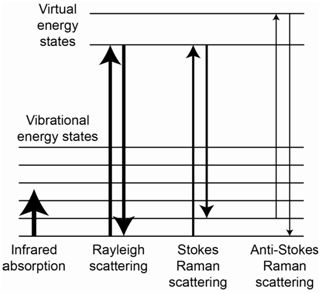
It is important to recognize that, while the processes in Figure \(\PageIndex{4}\) responsible for Raman scatter might look similar to the process of fluorescence, the process in Raman spectroscopy involves a modulated scatter that is different from fluorescence. How do we know this? One reason is that Raman scatter occurs when the incident radiation has energy well away from any absorption band of the molecule. Therefore, the molecule is not excited to some higher electronic state but instead exists in a virtual state that corresponds to a high energy vibrational state of the ground state. Another is that Raman scatter has a lifetime of 10^-14 second, which is much faster than fluorescent emission.

Which set of lines, Stokes or anti-Stokes, is weaker?

The anti-Stokes lines will be much weaker than the Stokes lines because there are many more molecules in the ground state than in excited vibrational states.

What effect would raising the temperature have on the intensity of Stokes and anti-Stokes lines?

Raising the temperature would decrease the population of the ground state and increase the population of higher energy vibrational states. Therefore, with increased temperature, the intensity of the Stokes lines would decrease and the intensity of the anti-Stokes lines would increase. However, the Stokes lines would still have higher intensity than the anti-Stokes lines.

Because scatter occurs in all directions, the scattered photons are measured at 90^o to the incident radiation. Also, Raman scatter is generally a rather unfavorable process resulting in a weak signal.

What would be the ideal source to use for measuring Raman spectra?

The more incident photons sent in to the sample, the more chance there is to produce molecules in the proper virtual state to produce Raman scattering. Since the signal is measured over no background, this suggests that we want a high power source. That means that a laser would be preferable as a source for measuring Raman spectra. The highly monochromatic emission from a laser also means that we can more accurately measure the frequency of the Stokes lines in the resulting spectrum. Also an array detector is preferable as it enables the simultaneous measurement of all of the scattered radiation.

The molecule carbon tetrachloride (CCl₄) has three Raman-active absorptions that occur at 218, 314 and 459 cm^-1 away from the laser line. Draw a representation of the Raman spectrum of CCl₄ that includes both the Stokes and anti-Stokes lines.

The spectrum in Figure \(\PageIndex{5}\) shows a representation of the complete Raman spectrum for carbon tetrachloride and includes the Stokes and anti-Stokes lines. The laser line undergoes an elastic scattering known as Rayleigh scatter and a complete spectrum has a peak at the laser line that is far more intense than the Raman scatter. Note that the anti-Stokes lines are lower in intensity and higher in energy than the Stokes lines. Note as well that the two spectra appear as mirror images of each other with regards to the placement of the bands at 218, 314 and 459 cm^-1 away from the Rayleigh scatter peak.

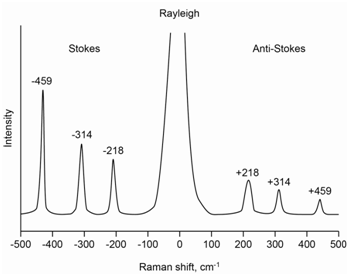
The energy level diagram in Figure \(\PageIndex{6}\) shows the origin of all of the lines and inspection of it should rationalize why the placement of the Stokes and anti-Stokes lines are mirror images of each other. The relative intensity of the three Stokes lines depends on the probability of each scatter process and is something we could not readily predict ahead of time.

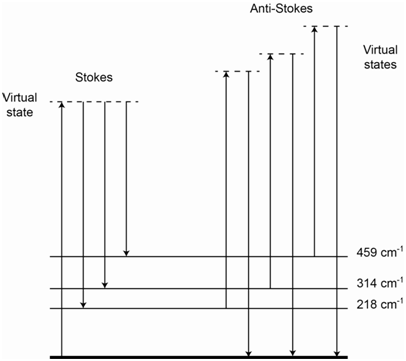
Why do the anti-Stokes lines of carbon tetrachloride have the following order of intensity: 219 > 314 > 459 cm^-1?

The intensity of the three anti-Stokes lines drops going from the 218 to 314 to 459 cm^-1 band. Anti-Stokes scatter requires an interaction of the incident photon with vibrationally excited molecules. Heat in the system causes some molecules to be vibrationally excited. The drop in intensity is predictable because, as the vibrational levels increase in energy, they would have lower populations and therefore fewer molecules to produce Raman scatter at that transition.

Raman spectroscopy is an important tool used in the characterization of many compounds. As we have already seen, because the selection rules for Raman (change in polarizability) are different than infrared (change in the dipole moment) spectroscopy, there are some vibrations that are active in one technique but not the other. Water is a weak Raman scatterer and, unlike infrared spectroscopy, where water has strong absorptions, water can be used as a solvent. Glass cells can be used with the visible laser radiation, which is more convenient that the salt plates that need to be used in infrared spectroscopy. Because Raman spectroscopy involves the measurement of vibrational energy states with visible light, it is especially useful for measurements of vibrational processes that occur in the far IR portion of the spectrum. Finally, since Raman spectroscopy involves a scattering process, it can be used for remote monitoring such as atmospheric monitoring. A pulsed laser can be passed through the atmosphere or effluent from a smoke stack and Raman scattered radiation measured by remote detectors.

One disadvantage of Raman spectroscopy is that Raman scatter is an unfavorable process and the signals are weak compared to many other spectroscopic methods. There are two strategies that have been found to significantly increase the probability of Raman scatter and lower the detection limits.

One is a technique known as surface-enhanced Raman spectroscopy (SERS). It is observed that compounds on surfaces consisting of roughened silver, gold or copper have much higher probability of producing Raman scatter. The other involves the use of resonance Raman spectroscopy. If the molecule is excited using a laser line close to an electronic absorption band, large enhancements in the Raman bands of symmetrical vibrations occur. As noted earlier, the lifetime of 10^-14 second of Raman scatter indicates that the increased signal is not from a fluorescent transition.