8.2: Precipitation Gravimetry
- Page ID
- 163749
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In precipitation gravimetry an insoluble compound forms when we add a precipitating reagent, or precipitant, to a solution that contains our analyte. In most cases the precipitate is the product of a simple metathesis reaction between the analyte and the precipitant; however, any reaction that generates a precipitate potentially can serve as a gravimetric method.
Most precipitation gravimetric methods were developed in the nineteenth century, or earlier, often for the analysis of ores. Figure 1.1.1 in Chapter 1, for example, illustrates a precipitation gravimetric method for the analysis of nickel in ores.
Theory and Practice
All precipitation gravimetric analyses share two important attributes. First, the precipitate must be of low solubility, of high purity, and of known composition if its mass is to reflect accurately the analyte’s mass. Second, it must be easy to separate the precipitate from the reaction mixture.
Solubility Considerations
To provide an accurate result, a precipitate’s solubility must be minimal. The accuracy of a total analysis technique typically is better than ±0.1%, which means the precipitate must account for at least 99.9% of the analyte. Extending this requirement to 99.99% ensures the precipitate’s solubility will not limit the accuracy of a gravimetric analysis.
A total analysis technique is one in which the analytical signal—mass in this case—is proportional to the absolute amount of analyte in the sample. See Chapter 3 for a discussion of the difference between total analysis techniques and concentration techniques.
We can minimize solubility losses by controlling the conditions under which the precipitate forms. This, in turn, requires that we account for every equilibrium reaction that might affect the precipitate’s solubility. For example, we can determine Ag+ gravimetrically by adding NaCl as a precipitant, forming a precipitate of AgCl.
\[\mathrm{Ag}^{+}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons\mathrm{AgCl}(s) \label{8.1}\]
If this is the only reaction we consider, then we predict that the precipitate’s solubility, SAgCl, is given by the following equation.
\[S_{\mathrm{AgCl}}=\left[\mathrm{Ag}^{+}\right]=\frac{K_{\mathrm{sp}}}{\left[\mathrm{Cl}^{-}\right]} \label{8.2}\]
Equation \ref{8.2} suggests that we can minimize solubility losses by adding a large excess of Cl–. In fact, as shown in Figure 8.2.1 , adding a large excess of Cl– increases the precipitate’s solubility.
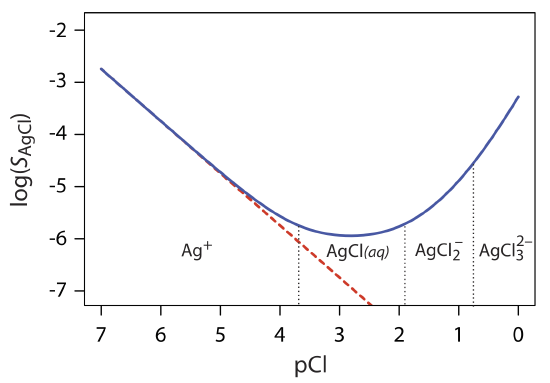
To understand why the solubility of AgCl is more complicated than the relationship suggested by Equation \ref{8.2}, we must recall that Ag+ also forms a series of soluble silver-chloro metal–ligand complexes.
\[\operatorname{Ag}^{+}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons\operatorname{AgCl}(a q) \quad \log K_{1}=3.70 \label{8.3}\]
\[\operatorname{AgCl}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons\operatorname{AgCl}_{2}(a q) \quad \log K_{2}=1.92 \label{8.4}\]
\[\mathrm{AgCl}_{2}^{-}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons\mathrm{AgCl}_{3}^{2-}(a q) \quad \log K_{3}=0.78 \label{8.5}\]
Note the difference between reaction \ref{8.3}, in which we form AgCl(aq) as a product, and reaction \ref{8.1}, in which we form AgCl(s) as a product. The formation of AgCl(aq) from AgCl(s)
\[\operatorname{AgCl}(s)\rightleftharpoons\operatorname{AgCl}(a q) \nonumber\]
is called AgCl’s intrinsic solubility.
The actual solubility of AgCl is the sum of the equilibrium concentrations for all soluble forms of Ag+.
\[S_{\mathrm{AgCl}}=\left[\mathrm{Ag}^{+}\right]+[\mathrm{AgCl}(a q)]+\left[\mathrm{AgCl}_{2}^-\right]+\left[\mathrm{AgCl}_{3}^{2-}\right] \label{8.6}\]
By substituting into Equation \ref{8.6} the equilibrium constant expressions for reaction \ref{8.1} and reactions \ref{8.3}–\ref{8.5}, we can define the solubility of AgCl as
\[S_\text{AgCl} = \frac {K_\text{sp}} {[\text{Cl}^-]} + K_1K_\text{sp} + K_1K_2K_\text{sp}[\text{Cl}^-]+K_1K_2K_3K_\text{sp}[\text{Cl}^-]^2 \label{8.7}\]
Equation \ref{8.7} explains the solubility curve for AgCl shown in Figure 8.2.1 . As we add NaCl to a solution of Ag+, the solubility of AgCl initially decreases because of reaction \ref{8.1}. Under these conditions, the final three terms in Equation \ref{8.7} are small and Equation \ref{8.2} is sufficient to describe AgCl’s solubility. For higher concentrations of Cl–, reaction \ref{8.4} and reaction \ref{8.5} increase the solubility of AgCl. Clearly the equilibrium concentration of chloride is important if we wish to determine the concentration of silver by precipitating AgCl. In particular, we must avoid a large excess of chloride.
The predominate silver-chloro complexes for different values of pCl are shown by the ladder diagram along the x-axis in Figure 8.2.1 . Note that the increase in solubility begins when the higher-order soluble complexes of \(\text{AgCl}_2^-\) and \(\text{AgCl}_3^{2-}\) are the predominate species.
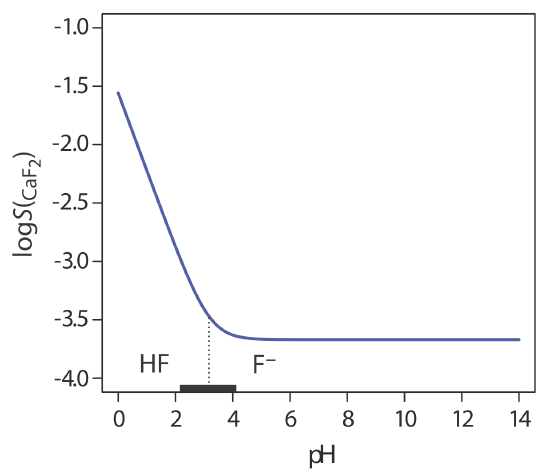
Another important parameter that may affect a precipitate’s solubility is pH. For example, a hydroxide precipitate, such as Fe(OH)3, is more soluble at lower pH levels where the concentration of OH– is small. Because fluoride is a weak base, the solubility of calcium fluoride, \(S_{\text{CaF}_2}\), also is pH-dependent. We can derive an equation for \(S_{\text{CaF}_2}\) by considering the following equilibrium reactions
\[\mathrm{CaF}_{2}(s)\rightleftharpoons \mathrm{Ca}^{2+}(a q)+2 \mathrm{F}^{-}(a q) \quad K_{\mathfrak{sp}}=3.9 \times 10^{-11} \label{8.8}\]
\[\mathrm{HF}(a q)+\mathrm{H}_{2} \mathrm{O}(l )\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{F}^{-}(a q) \quad K_{\mathrm{a}}=6.8 \times 10^{-4} \label{8.9}\]
and the following equation for the solubility of CaF2.
\[S_{\mathrm{Ca} \mathrm{F}_{2}}=\left[\mathrm{Ca}^{2+}\right]=\frac{1}{2}\left\{\left[\mathrm{F}^{-}\right]+[\mathrm{HF}]\right\} \label{8.10}\]
Be sure that Equation \ref{8.10} makes sense to you. Reaction \ref{8.8} tells us that the dissolution of CaF2 produces one mole of Ca2+ for every two moles of F–, which explains the term of 1/2 in Equation \ref{8.10}. Because F– is a weak base, we must account for both chemical forms in solution, which explains why we include HF.
Substituting the equilibrium constant expressions for reaction \ref{8.8} and reaction \ref{8.9} into Equation \ref{8.10} allows us to define the solubility of CaF2 in terms of the equilibrium concentration of H3O+.
\[S_{\mathrm{CaF}_{2}}=\left[\mathrm{Ca}^{2+}\right]=\left\{\frac{K_{\mathrm{p}}}{4}\left(1+\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{\mathrm{a}}}\right)^{2}\right\}^{1 / 3} \label{8.11}\]
Figure 8.2.2 shows how pH affects the solubility of CaF2. Depending on the solution’s pH, the predominate form of fluoride is either HF or F–. When the pH is greater than 4.17, the predominate species is F– and the solubility of CaF2 is independent of pH because only reaction \ref{8.8} occurs to an appreciable extent. At more acidic pH levels, the solubility of CaF2 increases because of the contribution of reaction \ref{8.9}.
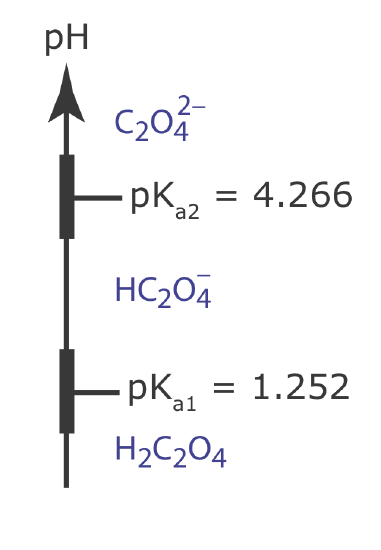
You can use a ladder diagram to predict the conditions that will minimize a precipitate’s solubility. Draw a ladder diagram for oxalic acid, H2C2O4, and use it to predict the range of pH values that will minimize the solubility of CaC2O4. Relevant equilibrium constants are in the appendices.
- Answer
-
The solubility reaction for CaC2O4 is
\[\mathrm{CaC}_{2} \mathrm{O}_{4}(s)\rightleftharpoons \mathrm{Ca}^{2+}(a q)+\mathrm{C}_{2} \mathrm{O}_{4}^{2-}(a q) \nonumber\]
To minimize solubility, the pH must be sufficiently basic that oxalate, \(\text{C}_2\text{O}_4^{2-}\), does not react to form \(\text{HC}_2\text{O}_4^{-}\) or H2C2O4. The ladder diagram for oxalic acid, including approximate buffer ranges, is shown below. Maintaining a pH greater than 5.3 ensures that \(\text{C}_2\text{O}_4^{2-}\) is the only important form of oxalic acid in solution, minimizing the solubility of CaC2O4.
When solubility is a concern, it may be possible to decrease solubility by using a non-aqueous solvent. A precipitate’s solubility generally is greater in an aqueous solution because of water’s ability to stabilize ions through solvation. The poorer solvating ability of a non-aqueous solvent, even those that are polar, leads to a smaller solubility product. For example, the Ksp of PbSO4 is \(2 \times 10^{-8}\) in H2O and \(2.6 \times 10^{-12}\) in a 50:50 mixture of H2O and ethanol.
Avoiding Impurities
In addition to having a low solubility, a precipitate must be free from impurities. Because precipitation usually occurs in a solution that is rich in dissolved solids, the initial precipitate often is impure. To avoid a determinate error, we must remove these impurities before we determine the precipitate’s mass.
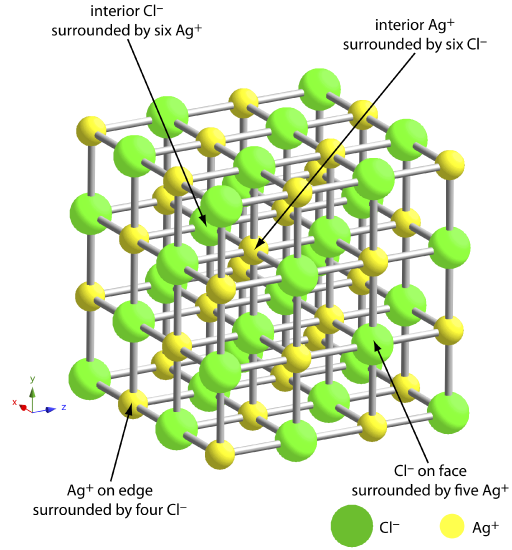
The greatest source of impurities are chemical and physical interactions that take place at the precipitate’s surface. A precipitate generally is crystalline—even if only on a microscopic scale—with a well-defined lattice of cations and anions. Those cations and anions at the precipitate’s surface carry, respectively, a positive or a negative charge because they have incomplete coordination spheres. In a precipitate of AgCl, for example, each silver ion in the precipitate’s interior is bound to six chloride ions. A silver ion at the surface, however, is bound to no more than five chloride ions and carries a partial positive charge (Figure 8.2.3 ). The presence of these partial charges makes the precipitate’s surface an active site for the chemical and physical interactions that produce impurities.
One common impurity is an inclusion, in which a potential interferent, whose size and charge is similar to a lattice ion, can substitute into the lattice structure if the interferent precipitates with the same crystal structure (Figure 8.2.4 a). The probability of forming an inclusion is greatest when the interfering ion’s concentration is substantially greater than the lattice ion’s concentration. An inclusion does not decrease the amount of analyte that precipitates, provided that the precipitant is present in sufficient excess. Thus, the precipitate’s mass always is larger than expected.
An inclusion is difficult to remove since it is chemically part of the precipitate’s lattice. The only way to remove an inclusion is through reprecipitation in which we isolate the precipitate from its supernatant solution, dissolve the precipitate by heating in a small portion of a suitable solvent, and then reform the precipitate by allowing the solution to cool. Because the interferent’s concentration after dissolving the precipitate is less than that in the original solution, the amount of included material decreases upon reprecipitation. We can repeat the process of reprecipitation until the inclusion’s mass is insignificant. The loss of analyte during reprecipitation, however, is a potential source of determinate error.
Suppose that 10% of an interferent forms an inclusion during each precipitation. When we initially form the precipitate, 10% of the original interferent is present as an inclusion. After the first reprecipitation, 10% of the included interferent remains, which is 1% of the original interferent. A second reprecipitation decreases the interferent to 0.1% of the original amount.
An occlusion forms when an interfering ions is trapped within the growing precipitate. Unlike an inclusion, which is randomly dispersed within the precipitate, an occlusion is localized, either along flaws within the precipitate’s lattice structure or within aggregates of individual precipitate particles (Figure 8.2.4 b). An occlusion usually increases a precipitate’s mass; however, the precipitate’s mass is smaller if the occlusion includes the analyte in a lower molecular weight form than that of the precipitate.
We can minimize an occlusion by maintaining the precipitate in equilibrium with its supernatant solution for an extended time, a process called digestion. During a digestion, the dynamic nature of the solubility–precipitation equilibria, in which the precipitate dissolves and reforms, ensures that the occlusion eventually is reexposed to the supernatant solution. Because the rates of dissolution and reprecipitation are slow, there is less opportunity for forming new occlusions.
After precipitation is complete the surface continues to attract ions from solution (Figure 8.2.4 c). These surface adsorbates comprise a third type of impurity. We can minimize surface adsorption by decreasing the precipitate’s available surface area. One benefit of digestion is that it increases a precipitate’s average particle size. Because the probability that a particle will dissolve completely is inversely proportional to its size, during digestion larger particles increase in size at the expense of smaller particles. One consequence of forming a smaller number of larger particles is an overall decrease in the precipitate’s surface area. We also can remove surface adsorbates by washing the precipitate, although we cannot ignore the potential loss of analyte.
Inclusions, occlusions, and surface adsorbates are examples of coprecipitates—otherwise soluble species that form along with the precipitate that contains the analyte. Another type of impurity is an interferent that forms an independent precipitate under the conditions of the analysis. For example, the precipitation of nickel dimethylglyoxime requires a slightly basic pH. Under these conditions any Fe3+ in the sample will precipitate as Fe(OH)3. In addition, because most precipitants rarely are selective toward a single analyte, there is a risk that the precipitant will react with both the analyte and an interferent.
In addition to forming a precipitate with Ni2+, dimethylglyoxime also forms precipitates with Pd2+ and Pt2+. These cations are potential interferents in an analysis for nickel.
We can minimize the formation of additional precipitates by controlling solution conditions. If an interferent forms a precipitate that is less soluble than the analyte’s precipitate, we can precipitate the interferent and remove it by filtration, leaving the analyte behind in solution. Alternatively, we can mask the analyte or the interferent to prevent its precipitation. Both of the approaches outline above are illustrated in Fresenius’ analytical method for the determination of Ni in ores that contain Pb2+, Cu2+, and Fe3+ (see Figure 1.1.1 in Chapter 1). Dissolving the ore in the presence of H2SO4 selectively precipitates Pb2+ as PbSO4. Treating the resulting supernatant with H2S precipitates Cu2+ as CuS. After removing the CuS by filtration, ammonia is added to precipitate Fe3+ as Fe(OH)3. Nickel, which forms a soluble amine complex, remains in solution.
Masking was introduced in Chapter 7.
Controlling Particle Size
Size matters when it comes to forming a precipitate. Larger particles are easier to filter and, as noted earlier, a smaller surface area means there is less opportunity for surface adsorbates to form. By controlling the reaction conditions we can significantly increase a precipitate’s average particle size.
The formation of a precipitate consists of two distinct events: nucleation, the initial formation of smaller, stable particles of the precipitate, and particle growth. Larger particles form when the rate of particle growth exceeds the rate of nucleation. Understanding the conditions that favor particle growth is important when we design a gravimetric method of analysis.
We define a solute’s relative supersaturation, RSS, as
\[R S S=\frac{Q-S}{S} \label{8.12}\]
where Q is the solute’s actual concentration and S is the solute’s concentration at equilibrium [Von Weimarn, P. P. Chem. Revs. 1925, 2, 217–242]. The numerator of Equation \ref{8.12}, Q – S, is a measure of the solute’s supersaturation. A solution with a large, positive value of RSS has a high rate of nucleation and produces a precipitate with many small particles. When the RSS is small, precipitation is more likely to occur by particle growth than by nucleation.
A supersaturated solution is one that contains more dissolved solute than that predicted by equilibrium chemistry. A supersaturated solution is inherently unstable and precipitates solute to reach its equilibrium position. How quickly precipitation occurs depends, in part, on the value of RSS.
Equation \ref{8.12} suggests that we can minimize RSS if we decrease the solute’s concentration, Q, or if we increase the precipitate’s solubility, S. A precipitate’s solubility usually increases at higher temperatures and adjusting pH may affect a precipitate’s solubility if it contains an acidic or a basic ion. Temperature and pH, therefore, are useful ways to increase the value of S. Forming the precipitate in a dilute solution of analyte or adding the precipitant slowly and with vigorous stirring are ways to decrease the value of Q.
There are practical limits to minimizing RSS. Some precipitates, such as Fe(OH)3 and PbS, are so insoluble that S is very small and a large RSS is unavoidable. Such solutes inevitably form small particles. In addition, conditions that favor a small RSS may lead to a relatively stable supersaturated solution that requires a long time to precipitate fully. For example, almost a month is required to form a visible precipitate of BaSO4 under conditions in which the initial RSS is 5 [Bassett, J.; Denney, R. C.; Jeffery, G. H. Mendham. J. Vogel’s Textbook of Quantitative Inorganic Analysis, Longman: London, 4th Ed., 1981, p. 408].
A visible precipitate takes longer to form when RSS is small both because there is a slow rate of nucleation and because there is a steady decrease in RSS as the precipitate forms. One solution to the latter problem is to generate the precipitant in situ as the product of a slow chemical reaction, which effectively maintains a constant RSS. Because the precipitate forms under conditions of low RSS, initial nucleation produces a small number of particles. As additional precipitant forms, particle growth supersedes nucleation, which results in larger particles of precipitate. This process is called a homogeneous precipitation [Gordon, L.; Salutsky, M. L.; Willard, H. H. Precipitation from Homogeneous Solution, Wiley: NY, 1959].
Two general methods are used for homogeneous precipitation. If the precipitate’s solubility is pH-dependent, then we can mix the analyte and the precipitant under conditions where precipitation does not occur, and then increase or decrease the pH by chemically generating OH– or H3O+. For example, the hydrolysis of urea, CO(NH2)2, is a source of OH– because of the following two reactions.
\[\mathrm{CO}\left(\mathrm{NH}_{2}\right)_{2}(a q)+\mathrm{H}_{2} \mathrm{O}( l)\rightleftharpoons2 \mathrm{NH}_{3}(a q)+\mathrm{CO}_{2}(g) \nonumber\]
\[\mathrm{NH}_{3}(a q)+\mathrm{H}_{2} \mathrm{O}( l)\rightleftharpoons\mathrm{OH}^{-}(a q)+\mathrm{NH}_{4}^{+}(a q) \nonumber\]
Because the hydrolysis of urea is temperature-dependent—the rate is negligible at room temperature—we can use temperature to control the rate of hydrolysis and the rate of precipitate formation. Precipitates of CaC2O4, for example, have been produced by this method. After dissolving a sample that contains Ca2+, the solution is made acidic with HCl before adding a solution of 5% w/v (NH4)2C2O4. Because the solution is acidic, a precipitate of CaC2O4 does not form. The solution is heated to approximately 50oC and urea is added. After several minutes, a precipitate of CaC2O4 begins to form, with precipitation reaching completion in about 30 min.
In the second method of homogeneous precipitation, the precipitant is generated by a chemical reaction. For example, Pb2+ is precipitated homogeneously as PbCrO4 by using bromate, \(\text{BrO}_3^-\), to oxidize Cr3+ to \(\text{CrO}_4^{2-}\).
\[6 \mathrm{BrO}_{3}^{-}(a q)+10 \mathrm{Cr}^{3+}(a q)+22 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons 3 \mathrm{Br}_{2}(a q)+10 \mathrm{CrO}_{4}^{2-}(a q)+44 \mathrm{H}^{+}(a q) \nonumber\]
Figure 8.2.5 shows the result of preparing PbCrO4 by direct addition of K2CrO4 (Beaker A) and by homogenous precipitation (Beaker B). Both beakers contain the same amount of PbCrO4. Because the direct addition of K2CrO4 leads to rapid precipitation and the formation of smaller particles, the precipitate remains less settled than the precipitate prepared homogeneously. Note, as well, the difference in the color of the two precipitates.

The effect of particle size on color is well-known to geologists, who use a streak test to help identify minerals. The color of a bulk mineral and its color when powdered often are different. Rubbing a mineral across an unglazed porcelain plate leaves behind a small streak of the powdered mineral. Bulk samples of hematite, Fe2O3, are black in color, but its streak is a familiar rust-red. Crocite, the mineral PbCrO4, is red-orange in color; its streak is orange-yellow.
A homogeneous precipitation produces large particles of precipitate that are relatively free from impurities. These advantages, however, are offset by the increased time needed to produce the precipitate and by a tendency for the precipitate to deposit as a thin film on the container’s walls. The latter problem is particularly severe for hydroxide precipitates generated using urea.
An additional method for increasing particle size deserves mention. When a precipitate’s particles are electrically neutral they tend to coagulate into larger particles that are easier to filter. Surface adsorption of excess lattice ions, however, provides the precipitate’s particles with a net positive or a net negative surface charge. Electrostatic repulsion between particles of similar charge prevents them from coagulating into larger particles.
Let’s use the precipitation of AgCl from a solution of AgNO3 using NaCl as a precipitant to illustrate this effect. Early in the precipitation, when NaCl is the limiting reagent, excess Ag+ ions chemically adsorb to the AgCl particles, forming a positively charged primary adsorption layer (Figure 8.2.6 a). The solution in contact with this layer contains more inert anions, \(\text{NO}_3^-\) in this case, than inert cations, Na+, giving a secondary adsorption layer with a negative charge that balances the primary adsorption layer’s positive charge. The solution outside the secondary adsorption layer remains electrically neutral. Coagulation cannot occur if the secondary adsorption layer is too thick because the individual particles of AgCl are unable to approach each other closely enough.
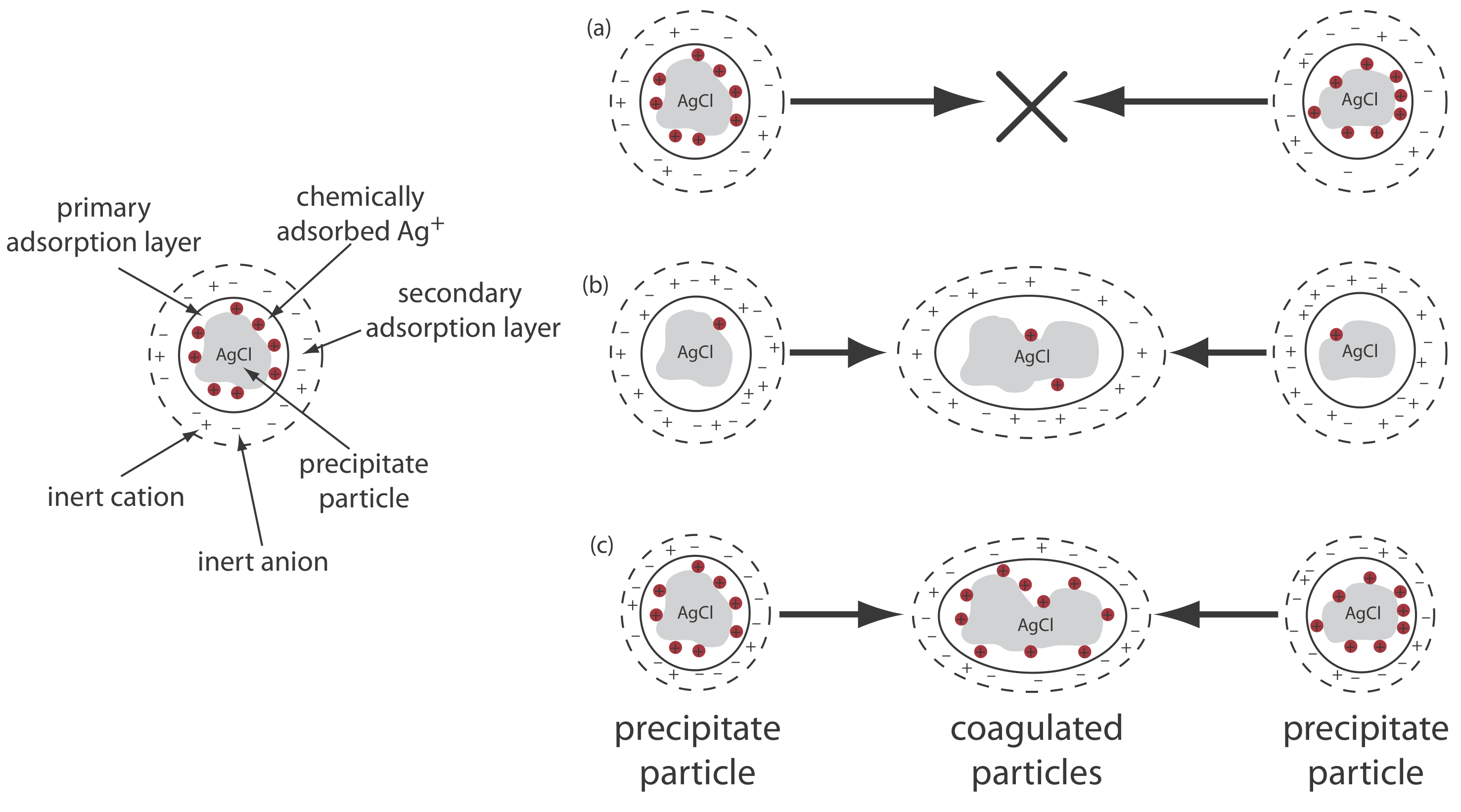
We can induce coagulation in three ways: by decreasing the number of chemically adsorbed Ag+ ions, by increasing the concentration of inert ions, or by heating the solution. As we add additional NaCl, precipitating more of the excess Ag+, the number of chemically adsorbed silver ions decreases and coagulation occurs (Figure 8.2.6 b). Adding too much NaCl, however, creates a primary adsorption layer of excess Cl– with a loss of coagulation.
The coagulation and decoagulation of AgCl as we add NaCl to a solution of AgNO3 can serve as an endpoint for a titration. See Chapter 9 for additional details.
A second way to induce coagulation is to add an inert electrolyte, which increases the concentration of ions in the secondary adsorption layer (Figure 8.2.6 c). With more ions available, the thickness of the secondary absorption layer decreases. Particles of precipitate may now approach each other more closely, which allows the precipitate to coagulate. The amount of electrolyte needed to cause spontaneous coagulation is called the critical coagulation concentration.
Heating the solution and the precipitate provides a third way to induce coagulation. As the temperature increases, the number of ions in the primary adsorption layer decreases, which lowers the precipitate’s surface charge. In addition, heating increases the particles’ kinetic energy, allowing them to overcome the electrostatic repulsion that prevents coagulation at lower temperatures.
Filtering the Precipitate
After precipitating and digesting a precipitate, we separate it from solution by filtering. The most common filtration method uses filter paper, which is classified according to its speed, its size, and its ash content on ignition. Speed, or how quickly the supernatant passes through the filter paper, is a function of the paper’s pore size. A larger pore size allows the supernatant to pass more quickly through the filter paper, but does not retain small particles of precipitate. Filter paper is rated as fast (retains particles larger than 20–25 μm), medium–fast (retains particles larger than 16 μm), medium (retains particles larger than 8 μm), and slow (retains particles larger than 2–3 μm). The proper choice of filtering speed is important. If the filtering speed is too fast, we may fail to retain some of the precipitate, which causes a negative determinate error. On the other hand, the precipitate may clog the pores if we use a filter paper that is too slow.
A filter paper’s size is just its diameter. Filter paper comes in many sizes, including 4.25 cm, 7.0 cm, 11.0 cm, 12.5 cm, 15.0 cm, and 27.0 cm. Choose a size that fits comfortably into your funnel. For a typical 65-mm long-stem funnel, 11.0 cm and 12.5 cm filter paper are good choices.
Because filter paper is hygroscopic, it is not easy to dry it to a constant weight. When accuracy is important, the filter paper is removed before we determine the precipitate’s mass. After transferring the precipitate and filter paper to a covered crucible, we heat the crucible to a temperature that coverts the paper to CO2(g) and H2O(g), a process called ignition.
Igniting a poor quality filter paper leaves behind a residue of inorganic ash. For quantitative work, use a low-ash filter paper. This grade of filter paper is pretreated with a mixture of HCl and HF to remove inorganic materials. Quantitative filter paper typically has an ash content of less than 0.010% w/w.
Gravity filtration is accomplished by folding the filter paper into a cone and placing it in a long-stem funnel (Figure 8.2.7 ). To form a tight seal between the filter cone and the funnel, we dampen the paper with water or supernatant and press the paper to the wall of the funnel. When prepared properly, the funnel’s stem fills with the supernatant, increasing the rate of filtration.
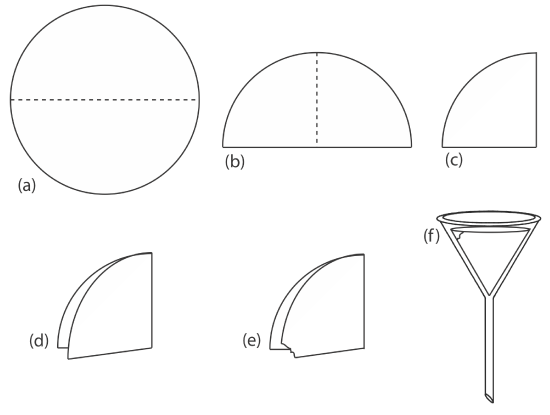
corner is torn off (e) before the paper is opened up into a cone and placed in the funnel (f ).
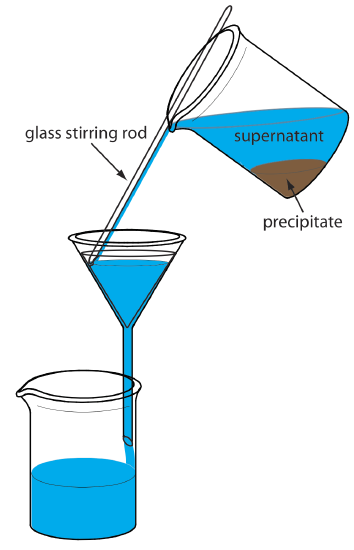
The precipitate is transferred to the filter in several steps. The first step is to decant the majority of the supernatant through the filter paper without transferring the precipitate (Figure 8.2.8 ). This prevents the filter paper from clogging at the beginning of the filtration process. The precipitate is rinsed while it remains in its beaker, with the rinsings decanted through the filter paper. Finally, the precipitate is transferred onto the filter paper using a stream of rinse solution. Any precipitate that clings to the walls of the beaker is transferred using a rubber policeman (a flexible rubber spatula attached to the end of a glass stirring rod).
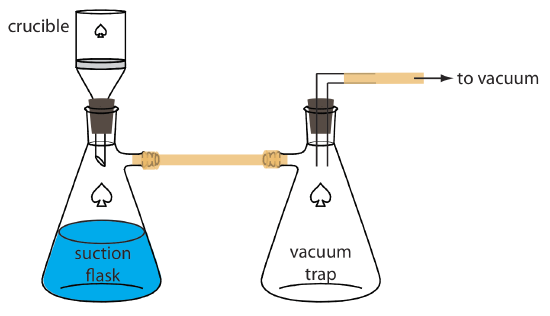
An alternative method for filtering a precipitate is to use a filtering crucible. The most common option is a fritted-glass crucible that contains a porous glass disk filter. Fritted-glass crucibles are classified by their porosity: coarse (retaining particles larger than 40–60 μm), medium (retaining particles greater than 10–15 μm), and fine (retaining particles greater than 4–5.5 μm). Another type of filtering crucible is the Gooch crucible, which is a porcelain crucible with a perforated bottom. A glass fiber mat is placed in the crucible to retain the precipitate. For both types of crucibles, the pre- cipitate is transferred in the same manner described earlier for filter paper. Instead of using gravity, the supernatant is drawn through the crucible with the assistance of suction from a vacuum aspirator or pump (Figure 8.2.9 ).
Rinsing the Precipitate
Because the supernatant is rich with dissolved inert ions, we must remove residual traces of supernatant without incurring loss of analyte due to solubility. In many cases this simply involves the use of cold solvents or rinse solutions that contain organic solvents such as ethanol. The pH of the rinse solution is critical if the precipitate contains an acidic or a basic ion. When coagulation plays an important role in determining particle size, adding a volatile inert electrolyte to the rinse solution prevents the precipitate from reverting into smaller particles that might pass through the filter. This process of reverting to smaller particles is called peptization. The volatile electrolyte is removed when drying the precipitate.
In general, we can minimize the loss of analyte if we use several small portions of rinse solution instead of a single large volume. Testing the used rinse solution for the presence of an impurity is another way to guard against over-rinsing the precipitate. For example, if Cl– is a residual ion in the supernatant, we can test for its presence using AgNO3. After we collect a small portion of the rinse solution, we add a few drops of AgNO3 and look for the presence or absence of a precipitate of AgCl. If a precipitate forms, then we know Cl– is present and continue to rinse the precipitate. Additional rinsing is not needed if the AgNO3 does not produce a precipitate.
Drying the Precipitate
After separating the precipitate from its supernatant solution, we dry the precipitate to remove residual traces of rinse solution and to remove any volatile impurities. The temperature and method of drying depend on the method of filtration and the precipitate’s desired chemical form. Placing the precipitate in a laboratory oven and heating to a temperature of 110oC is sufficient to remove water and other easily volatilized impurities. Higher temperatures require a muffle furnace, a Bunsen burner, or a Meker burner, and are necessary if we need to decompose the precipitate before its weight is determined.
Because filter paper absorbs moisture, we must remove it before we weigh the precipitate. This is accomplished by folding the filter paper over the precipitate and transferring both the filter paper and the precipitate to a porcelain or platinum crucible. Gentle heating first dries and then chars the filter paper. Once the paper begins to char, we slowly increase the temperature until there is no trace of the filter paper and any remaining carbon is oxidized to CO2.
Fritted-glass crucibles can not withstand high temperatures and are dried in an oven at a temperature below 200oC. The glass fiber mats used in Gooch crucibles can be heated to a maximum temperature of approximately 500oC.
Composition of the Final Precipitate
For a quantitative application, the final precipitate must have a well-defined composition. A precipitate that contains volatile ions or substantial amounts of hydrated water, usually is dried at a temperature that completely removes these volatile species. For example, one standard gravimetric method for the determination of magnesium involves its precipitation as MgNH4PO4•6H2O. Unfortunately, this precipitate is difficult to dry at lower temperatures without losing an inconsistent amount of hydrated water and ammonia. Instead, the precipitate is dried at a temperature greater than 1000oC where it decomposes to magnesium pyrophosphate, Mg2P2O7.
An additional problem is encountered if the isolated solid is nonstoichiometric. For example, precipitating Mn2+ as Mn(OH)2 and heating frequently produces a nonstoichiometric manganese oxide, MnOx, where x varies between one and two. In this case the nonstoichiometric product is the result of forming a mixture of oxides with different oxidation state of manganese. Other nonstoichiometric compounds form as a result of lattice defects in the crystal structure [Ward, R., ed., Non-Stoichiometric Compounds (Ad. Chem. Ser. 39), American Chemical Society: Washington, D. C., 1963].
Representative Method 8.2.1: Determination of Mg in Water and Wastewater
The best way to appreciate the theoretical and practical details discussed in this section is to carefully examine a typical precipitation gravimetric method. Although each method is unique, the determination of Mg2+ in water and wastewater by precipitating MgNH4PO4• 6H2O and isolating Mg2P2O7 provides an instructive example of a typical procedure. The description here is based on Method 3500-Mg D in Standard Methods for the Examination of Water and Wastewater, 19th Ed., American Public Health Asso- ciation: Washington, D. C., 1995. With the publication of the 20th Edition in 1998, this method is no longer listed as an approved method.
Description of Method
Magnesium is precipitated as MgNH4PO4•6H2O using (NH4)2HPO4 as the precipitant. The precipitate’s solubility in a neutral solution is relatively high (0.0065 g/100 mL in pure water at 10oC), but it is much less soluble in the presence of dilute ammonia (0.0003 g/100 mL in 0.6 M NH3). Because the precipitant is not selective, a preliminary separation of Mg2+ from potential interferents is necessary. Calcium, which is the most significant interferent, is removed by precipitating it as CaC2O4. The presence of excess ammonium salts from the precipitant, or from the addition of too much ammonia, leads to the formation of Mg(NH4)4(PO4)2, which forms Mg(PO3)2 after drying. The precipitate is isolated by gravity filtration, using a rinse solution of dilute ammonia. After filtering, the precipitate is converted to Mg2P2O7 and weighed.
Procedure
Transfer a sample that contains no more than 60 mg of Mg2+ into a 600-mL beaker. Add 2–3 drops of methyl red indicator, and, if necessary, adjust the volume to 150 mL. Acidify the solution with 6 M HCl and add 10 mL of 30% w/v (NH4)2HPO4. After cooling and with constant stirring, add concentrated NH3 dropwise until the methyl red indicator turns yellow (pH > 6.3). After stirring for 5 min, add 5 mL of concentrated NH3 and continue to stir for an additional 10 min. Allow the resulting solution and precipitate to stand overnight. Isolate the precipitate by filtering through filter paper, rinsing with 5% v/v NH3. Dissolve the precipitate in 50 mL of 10% v/v HCl and precipitate a second time following the same procedure. After filtering, carefully remove the filter paper by charring. Heat the precipitate at 500oC until the residue is white, and then bring the precipitate to constant weight at 1100oC.
Questions
1. Why does the procedure call for a sample that contains no more than 60 mg of Mg2+?
A 60-mg portion of Mg2+ generates approximately 600 mg of MgNH4PO4•6H2O, which is a substantial amount of precipitate. A larger quantity of precipitate is difficult to filter and difficult to rinse free of impurities.
2. Why is the solution acidified with HCl before we add the precipitant?
The HCl ensures that MgNH4PO4 • 6H2O does not precipitate immediately upon adding the precipitant. Because \(\text{PO}_4^{3-}\) is a weak base, the precipitate is soluble in a strongly acidic solution. If we add the precipitant under neutral or basic conditions (that is, a high RSS), then the resulting precipitate will consist of smaller, less pure particles. Increasing the pH by adding base allows the precipitate to form under more favorable (that is, a low RSS) conditions.
3. Why is the acid–base indicator methyl red added to the solution?
The indicator changes color at a pH of approximately 6.3, which indicates that there is sufficient NH3 to neutralize the HCl added at the beginning of the procedure. The amount of NH3 is crucial to this procedure. If we add insufficient NH3, then the solution is too acidic, which increases the precipitate’s solubility and leads to a negative determinate error. If we add too much NH3, the precipitate may contain traces of Mg(NH4)4(PO4)2, which, on drying, forms Mg(PO3)2 instead of Mg2P2O7. This increases the mass of the ignited precipitate, and gives a positive determinate error. After adding enough NH3 to neutralize the HCl, we add an additional 5 mL of NH3 to complete the quantitative precipitation of MgNH4PO4 • 6H2O.
4. Explain why forming Mg(PO3)2 instead of Mg2P2O7 increases the precipitate’s mass.
Each mole of Mg2P2O7 contains two moles of magnesium and each mole of Mg(PO3)2 contains only one mole of magnesium. A conservation of mass, therefore, requires that two moles of Mg(PO3)2 form in place of each mole of Mg2P2O7. One mole of Mg2P2O7 weighs 222.6 g. Two moles of Mg(PO3)2 weigh 364.5 g. Any replacement of Mg2P2O7 with Mg(PO3)2 must increase the precipitate’s mass.
5. What additional steps, beyond those discussed in questions 2 and 3, help improve the precipitate’s purity?
Two additional steps in the procedure help to form a precipitate that is free of impurities: digestion and reprecipitation.
6. Why is the precipitate rinsed with a solution of 5% v/v NH3?
This is done for the same reason that the precipitation is carried out in an ammonical solution; using dilute ammonia minimizes solubility losses when we rinse the precipitate.
Quantitative Applications
Although no longer a common analytical technique, precipitation gravimetry still provides a reliable approach for assessing the accuracy of other methods of analysis, or for verifying the composition of standard reference materials. In this section we review the general application of precipitation gravimetry to the analysis of inorganic and organic compounds.
Inorganic Analysis
Table 8.2.1 provides a summary of precipitation gravimetric methods for inorganic cations and anions. Several methods for the homogeneous generation of precipitants are shown in Table 8.2.2 . The majority of inorganic precipitants show poor selectivity for the analyte. Many organic precipitants, however, are selective for one or two inorganic ions. Table 8.2.3 lists examples of several common organic precipitants.
Precipitation gravimetry continues to be listed as a standard method for the determination of \(\text{SO}_4^{2-}\) in water and wastewater analysis [Method 4500-SO42– C and Method 4500-SO42– D as published in Standard Methods for the Examination of Waters and Wastewaters, 20th Ed., American Public Health Association: Wash- ington, D. C., 1998]. Precipitation is carried out using BaCl2 in an acidic solution (adjusted with HCl to a pH of 4.5–5.0) to prevent the precipitation of BaCO3 or Ba3(PO4)2, and at a temperature near the solution’s boiling point. The precipitate is digested at 80–90oC for at least two hours. Ashless filter paper pulp is added to the precipitate to aid in its filtration. After filtering, the precipitate is ignited to constant weight at 800oC. Alternatively, the precipitate is filtered through a fine porosity fritted glass crucible (without adding filter paper pulp), and dried to constant weight at 105oC. This procedure is subject to a variety of errors, including occlusions of Ba(NO3)2, BaCl2, and alkali sulfates.
Other standard methods for the determination of sulfate in water and wastewater include ion chromatography (see Chapter 12), capillary ion electrophoresis (see Chapter 12), turbidimetry (see Chapter 10), and flow injection analysis (see Chapter 13).
Organic Analysis
Several organic functional groups or heteroatoms can be determined using precipitation gravimetric methods. Table 8.2.4 provides a summary of several representative examples. Note that the determination of alkoxy functional groups is an indirect analysis in which the functional group reacts with and excess of HI and the unreacted I– determined by precipitating as AgCl.
Quantitative Calculations
The stoichiometry of a precipitation reaction provides a mathematical relationship between the analyte and the precipitate. Because a precipitation gravimetric method may involve additional chemical reactions to bring the analyte into a different chemical form, knowing the stoichiometry of the precipitation reaction is not always sufficient. Even if you do not have a complete set of balanced chemical reactions, you can use a conservation of mass to deduce the mathematical relationship between the analyte and the precipitate. The following example demonstrates this approach for the direct analysis of a single analyte.
To determine the amount of magnetite, Fe3O4, in an impure ore, a 1.5419-g sample is dissolved in concentrated HCl, resulting in a mixture of Fe2+and Fe3+. After adding HNO3 to oxidize Fe2+ to Fe3+ and diluting with water, Fe3+ is precipitated as Fe(OH)3 using NH3. Filtering, rinsing, and igniting the precipitate provides 0.8525 g of pure Fe2O3. Calculate the %w/w Fe3O4 in the sample.
Solution
A conservation of mass requires that the precipitate of Fe2O3 contain all iron originally in the sample of ore. We know there are 2 moles of Fe per mole of Fe2O3 (FW = 159.69 g/mol) and 3 moles of Fe per mole of Fe3O4 (FW = 231.54 g/mol); thus
\[0.8525 \ \mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3} \times \frac{2 \ \mathrm{mol} \ \mathrm{Fe}}{159.69 \ \mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3}} \times \frac{231.54 \ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4}}{3 \ \mathrm{mol} \ \mathrm{Fe}}=0.82405 \ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4} \nonumber\]
The % w/w Fe3O4 in the sample, therefore, is
\[\frac{0.82405 \ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4}}{1.5419 \ \mathrm{g} \ \text { sample }} \times 100=53.44 \% \nonumber\]
A 0.7336-g sample of an alloy that contains copper and zinc is dissolved in 8 M HCl and diluted to 100 mL in a volumetric flask. In one analysis, the zinc in a 25.00-mL portion of the solution is precipitated as ZnNH4PO4, and isolated as Zn2P2O7, yielding 0.1163 g. The copper in a separate 25.00-mL portion of the solution is treated to precipitate CuSCN, yielding 0.2383 g. Calculate the %w/w Zn and the %w/w Cu in the sample.
- Answer
-
A conservation of mass requires that all zinc in the alloy is found in the final product, Zn2P2O7. We know there are 2 moles of Zn per mole of Zn2P2O7; thus
\[0.1163 \ \mathrm{g} \ \mathrm{Zn}_{2} \mathrm{P}_{2} \mathrm{O}_{7} \times \frac{2 \ \mathrm{mol} \ \mathrm{Zn}}{304.70 \ \mathrm{g}\ \mathrm{Zn}_{2} \mathrm{P}_{2} \mathrm{O}_{7}} \times \frac{65.38 \ \mathrm{g} \ \mathrm{Zn}}{\mathrm{mol} \ \mathrm{Zn}}=0.04991 \ \mathrm{g} \ \mathrm{Zn}\nonumber\]
This is the mass of Zn in 25% of the sample (a 25.00 mL portion of the 100.0 mL total volume). The %w/w Zn, therefore, is
\[\frac{0.04991 \ \mathrm{g} \ \mathrm{Zn} \times 4}{0.7336 \ \mathrm{g} \text { sample }} \times 100=27.21 \% \ \mathrm{w} / \mathrm{w} \mathrm{Zn} \nonumber\]
For copper, we find that
\[\begin{array}{c}{0.2383 \ \mathrm{g} \ \mathrm{CuSCN} \times \frac{1 \ \mathrm{mol} \ \mathrm{Zn}}{121.63 \ \mathrm{g} \ \mathrm{CuSCN}} \times \frac{63.55 \ \mathrm{g} \ \mathrm{Cu}}{\mathrm{mol} \ \mathrm{Cu}}=0.1245 \ \mathrm{g} \ \mathrm{Cu}} \\ {\frac{0.1245 \ \mathrm{g} \ \mathrm{Cu} \times 4}{0.7336 \ \mathrm{g} \text { sample }} \times 100=67.88 \% \ \mathrm{w} / \mathrm{w} \mathrm{Cu}}\end{array} \nonumber\]
In Practice Exercise 8.2.2 the sample contains two analytes. Because we can precipitate each analyte selectively, finding their respective concentrations is a straightforward stoichiometric calculation. But what if we cannot separately precipitate the two analytes? To find the concentrations of both analytes, we still need to generate two precipitates, at least one of which must contain both analytes. Although this complicates the calculations, we can still use a conservation of mass to solve the problem.
A 0.611-g sample of an alloy that contains Al and Mg is dissolved and treated to prevent interferences by the alloy’s other constituents. Aluminum and magnesium are precipitated using 8-hydroxyquinoline, which yields a mixed precipitate of Al(C9H6NO)3 and Mg(C9H6NO)2 that weighs 7.815 g. Igniting the precipitate converts it to a mixture of Al2O3 and MgO that weighs 1.002 g. Calculate the %w/w Al and %w/w Mg in the alloy.
Solution
The masses of the solids provide us with the following two equations.
\[\mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}+ \ \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=7.815 \ \mathrm{g} \nonumber\]
\[\mathrm{g} \ \mathrm{Al}_{2} \mathrm{O}_{3}+\mathrm{g} \ \mathrm{MgO}=1.002 \ \mathrm{g} \nonumber\]
With two equations and four unknowns, we need two additional equations to solve the problem. A conservation of mass requires that all the aluminum in Al(C9H6NO)3 also is in Al2O3; thus
\[\mathrm{g} \ \mathrm{Al}_{2} \mathrm{O}_{3}=\mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3} \times \frac{1 \ \mathrm{mol} \ \mathrm{Al}}{459.43 \ \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}} \times \frac{101.96 \ \mathrm{g} \ \mathrm{Al}_{2} \mathrm{O}_{3}}{2 \ \mathrm{mol} \ \mathrm{Al}_{2} \mathrm{O}_{3}} \nonumber\]
\[\mathrm{g} \ \mathrm{Al}_{2} \mathrm{O}_{3}=0.11096 \times \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3} \nonumber\]
Using the same approach, a conservation of mass for magnesium gives
\[\mathrm{g} \ \mathrm{MgO}=\mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2} \times \frac{1 \ \mathrm{mol} \ \mathrm{Mg}}{312.61 \ \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}} \times \frac{40.304 \ \mathrm{g} \ \mathrm{MgO}}{\mathrm{mol} \ \mathrm{MgO}} \nonumber\]
\[\mathrm{g} \ \mathrm{MgO}=0.12893 \times \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2} \nonumber\]
Substituting the equations for g MgO and g Al2O3 into the equation for the combined weights of MgO and Al2O3 leaves us with two equations and two unknowns.
\[\mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}+\mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=7.815 \ \mathrm{g} \nonumber\]
\[0.11096 \times \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}+ 0.12893 \times \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=1.002 \ \mathrm{g} \nonumber\]
Multiplying the first equation by 0.11096 and subtracting the second equation gives
\[-0.01797 \times \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=-0.1348 \ \mathrm{g} \nonumber\]
\[\mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=7.504 \ \mathrm{g} \nonumber\]
\[\mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}=7.815 \ \mathrm{g}-7.504 \ \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}, \mathrm{H}_{6} \mathrm{NO}\right)_{2}=0.311 \ \mathrm{g} \nonumber\]
Now we can finish the problem using the approach from Example 8.2.1 . A conservation of mass requires that all the aluminum and magnesium in the original sample of Dow metal is in the precipitates of Al(C9H6NO)3 and the Mg(C9H6NO)2. For aluminum, we find that
\[0.311 \ \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3} \times \frac{1 \ \mathrm{mol} \ \mathrm{Al}}{459.45 \ \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}} \times \frac{26.982 \ \mathrm{g} \ \mathrm{Al}}{\mathrm{mol} \ \mathrm{Al}}=0.01826 \ \mathrm{g} \ \mathrm{Al} \nonumber\]
\[\frac{0.01826 \ \mathrm{g} \ \mathrm{Al}}{0.611 \ \mathrm{g} \text { sample }} \times 100=2.99 \% \mathrm{w} / \mathrm{w} \mathrm{Al} \nonumber\]
and for magnesium we have
\[7.504 \ \text{g Mg}\left(\mathrm{C}_9 \mathrm{H}_{6} \mathrm{NO}\right)_{2} \times \frac{1 \ \mathrm{mol} \ \mathrm{Mg}}{312.61 \ \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_9 \mathrm{H}_{6} \mathrm{NO}\right)_{2}} \times \frac{24.305 \ \mathrm{g} \ \mathrm{Mg}}{\mathrm{mol} \ \mathrm{MgO}}=0.5834 \ \mathrm{g} \ \mathrm{Mg} \nonumber\]
\[\frac{0.5834 \ \mathrm{g} \ \mathrm{Mg}}{0.611 \ \mathrm{g} \text { sample }} \times 100=95.5 \% \mathrm{w} / \mathrm{w} \mathrm{Mg} \nonumber\]
A sample of a silicate rock that weighs 0.8143 g is brought into solution and treated to yield a 0.2692-g mixture of NaCl and KCl. The mixture of chloride salts is dissolved in a mixture of ethanol and water, and treated with HClO4, precipitating 0.3314 g of KClO4. What is the %w/w Na2O in the silicate rock?
- Answer
-
The masses of the solids provide us with the following equations
\[\mathrm{g} \ \mathrm{NaCl}+\mathrm{g} \ \mathrm{KCl}=0.2692 \ \mathrm{g} \nonumber\]
\[\mathrm{g} \ \mathrm{KClO}_{4} = 0.3314 \ \mathrm{g} \nonumber\]
With two equations are three unknowns—g NaCl, g KCl, and g KClO4—we need one additional equation to solve the problem. A conservation of mass requires that all the potassium originally in the KCl ends up in the KClO4; thus
\[\text{g KClO}_4 = \text{g KCl} \times \frac{1 \text{ mol Cl}}{74.55 \text{ g KCl}} \times \frac {138.55 \text{ g KClO}_4}{\text{mol Cl}} = 1.8585 \times \text{ g KCl} \nonumber\]
Given the mass of KClO4, we use the third equation to solve for the mass of KCl in the mixture of chloride salts
\[\text{ g KCl} = \frac{\text{g KClO}_4}{1.8585} = \frac{0.3314 \text{ g}}{1.8585} = 0.1783 \text{ g KCl} \nonumber\]
The mass of NaCl in the mixture of chloride salts, therefore, is
\[\text{ g NaCl} = 0.2692 \text{ g} - \text{g KCl} = 0.2692 \text{ g} - 0.1783 \text{ g KCl} = 0.0909 \text{ g NaCl} \nonumber\]
Finally, to report the %w/w Na2O in the sample, we use a conservation of mass on sodium to determine the mass of Na2O
\[0.0909 \text{ g NaCl} \times \frac{1 \text{ mol Na}}{58.44 \text{ g NaCl}} \times \frac{61.98 \text{ g Na}_2\text{O}}{2 \text{ mol Na}} = 0.0482 \text{ g Na}_2\text{O} \nonumber\]
giving the %w/w Na2O as
\[\frac{0.0482 \text{ g Na}_2\text{O}}{0.8143 \text{ g sample}} \times 100 = 5.92\% \text{ w/w Na}_2\text{O} \nonumber\]
The previous problems are examples of direct methods of analysis because the precipitate contains the analyte. In an indirect analysis the precipitate forms as a result of a reaction with the analyte, but the analyte is not part of the precipitate. As shown by the following example, despite the additional complexity, we still can use conservation principles to organize our calculations.
An impure sample of Na3PO3 that weighs 0.1392 g is dissolved in 25 mL of water. A second solution that contains 50 mL of 3% w/v HgCl2, 20 mL of 10% w/v sodium acetate, and 5 mL of glacial acetic acid is prepared. Adding the solution that contains the sample to the second solution oxidizes \(\text{PO}_3^{3-}\) to \(\text{PO}_4^{3-}\) and precipitates Hg2Cl2. After digesting, filtering, and rinsing the precipitate, 0.4320 g of Hg2Cl2 is obtained. Report the purity of the original sample as % w/w Na3PO3.
Solution
This is an example of an indirect analysis because the precipitate, Hg2Cl2, does not contain the analyte, Na3PO3. Although the stoichiometry of the reaction between Na3PO3 and HgCl2 is given earlier in the chapter, let’s see how we can solve the problem using conservation principles. (Although you can write the balanced reactions for any analysis, applying conservation principles can save you a significant amount of time!)
The reaction between Na3PO3 and HgCl2 is an oxidation-reduction reaction in which phosphorous increases its oxidation state from +3 in Na3PO3 to +5 in Na3PO4, and in which mercury decreases its oxidation state from +2 in HgCl2 to +1 in Hg2Cl2. A redox reaction must obey a conservation of electrons because all the electrons released by the reducing agent, Na3PO3, must be accepted by the oxidizing agent, HgCl2. Knowing this, we write the following stoichiometric conversion factors:
\[\frac{2 \ \mathrm{mol} \ e^{-}}{\mathrm{mol} \ \mathrm{Na}_{3} \mathrm{PO}_{3}} \text { and } \frac{1 \mathrm{mol} \ e^{-}}{\mathrm{mol} \ \mathrm{HgCl}_{2}} \nonumber\]
Now we are ready to solve the problem. First, we use a conservation of mass for mercury to convert the precipitate’s mass to the moles of HgCl2.
\[0.4320 \ \mathrm{g} \ \mathrm{Hg}_{2} \mathrm{Cl}_{2} \times \frac{2 \ \mathrm{mol} \ \mathrm{Hg}}{472.09 \ \mathrm{g} \ \mathrm{Hg}_{2} \mathrm{Cl}_{2}} \times \frac{1 \ \mathrm{mol} \ \mathrm{HgCl}_{2}}{\mathrm{mol} \ \mathrm{Hg}}=1.8302 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HgCl}_{2} \nonumber\]
Next, we use the conservation of electrons to find the mass of Na3PO3.
\[1.8302 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HgCl}_{2} \times \frac{1 \ \mathrm{mol} \ e^{-}}{\mathrm{mol} \ \mathrm{HgCl}_{2}} \times \frac{1 \ \mathrm{mol} \ \mathrm{Na}_{3} \mathrm{PO}_{4}}{2 \ \mathrm{mol} \ e^{-}} \times \frac{147.94 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{3}}{\mathrm{mol} \ \mathrm{Na}_{3} \mathrm{PO}_{3}}=0.13538 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{3} \nonumber\]
Finally, we calculate the %w/w Na3PO3 in the sample.
\[\frac{0.13538 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{3}}{0.1392 \ \mathrm{g} \text { sample }} \times 100=97.26 \% \mathrm{w} / \mathrm{w} \mathrm{Na}_{3} \mathrm{PO}_{3} \nonumber\]
As you become comfortable using conservation principles, you will see ways to further simplify problems. For example, a conservation of electrons requires that the electrons released by Na3PO3 end up in the product, Hg2Cl2, yielding the following stoichiometric conversion factor:
\[\frac{2 \ \operatorname{mol} \ \mathrm{Na}_{3} \mathrm{PO}_{3}}{\mathrm{mol} \ \mathrm{Hg}_{2} \mathrm{Cl}_{2}} \nonumber\]
This conversion factor provides a direct link between the mass of Hg2Cl2 and the mass of Na3PO3.
One approach for determining phosphate, \(\text{PO}_4^{3-}\), is to precipitate it as ammonium phosphomolybdate, (NH4)3PO4•12MoO3. After we isolate the precipitate by filtration, we dissolve it in acid and precipitate and weigh the molybdate as PbMoO3. Suppose we know that our sample is at least 12.5% Na3PO4 and that we need to recover a minimum of 0.600 g of PbMoO3? What is the minimum amount of sample that we need for each analysis?
- Answer
-
To find the mass of (NH4)3PO4•12MoO3 that will produce 0.600 g of PbMoO3, we first use a conservation of mass for molybdenum; thus
\[0.600 \ \mathrm{g} \ \mathrm{PbMoO}_{3} \times \frac{1 \ \mathrm{mol} \ \mathrm{Mo}}{351.2 \ \mathrm{g} \ \mathrm{PbMoO}_{3}} \times \frac{1876.59 \ \mathrm{g} \ \left(\mathrm{NH}_{4}\right)_{3} \mathrm{PO}_{4} \cdot 12 \mathrm{MoO}_{3}}{12 \ \mathrm{mol} \ \mathrm{Mo}}= 0.2672 \ \mathrm{g} \ \left(\mathrm{NH}_{4}\right)_{3} \mathrm{PO}_{4} \cdot 12 \mathrm{MoO}_{3} \nonumber\]
Next, to convert this mass of (NH4)3PO4•12MoO3 to a mass of Na3PO4, we use a conservation of mass on \(\text{PO}_4^{3-}\).
\[0.2672 \ \mathrm{g} \ \left(\mathrm{NH}_{4}\right)_{3} \mathrm{PO}_{4} \cdot 12 \mathrm{MoO}_{3} \times \frac{1 \ \mathrm{mol} \ \mathrm{PO}_{4}^{3-}}{1876.59 \ \mathrm{g \ }\left(\mathrm{NH}_{4}\right)_{3} \mathrm{PO}_{4} \cdot 12 \mathrm{MoO}_{3}} \times \frac{163.94 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{4}}{\mathrm{mol} \ \mathrm{PO}_{4}^{3-}}=0.02334 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{4} \nonumber\]
Finally, we convert this mass of Na3PO4 to the corresponding mass of sample.
\[0.02334 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{4} \times \frac{100 \ \mathrm{g} \text { sample }}{12.5 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{4}}=0.187 \ \mathrm{g} \text { sample } \nonumber\]
A sample of 0.187 g is sufficient to guarantee that we recover a minimum of 0.600 g PbMoO3. If a sample contains more than 12.5% Na3PO4, then a 0.187-g sample will produce more than 0.600 g of PbMoO3.
Qualitative Applications
A precipitation reaction is a useful method for identifying inorganic and organic analytes. Because a qualitative analysis does not require quantitative measurements, the analytical signal is simply the observation that a precipitate forms. Although qualitative applications of precipitation gravimetry have been replaced by spectroscopic methods of analysis, they continue to find application in spot testing for the presence of specific analytes [Jungreis, E. Spot Test Analysis; 2nd Ed., Wiley: New York, 1997].
Any of the precipitants listed in Table 8.2.1 , Table 8.2.3 , and Table 8.2.4 can be used for a qualitative analysis.
Evaluating Precipitation Gravimetry
Scale of Operation
The scale of operation for precipitation gravimetry is limited by the sensitivity of the balance and the availability of sample. To achieve an accuracy of ±0.1% using an analytical balance with a sensitivity of ±0.1 mg, we must isolate at least 100 mg of precipitate. As a consequence, precipitation gravimetry usually is limited to major or minor analytes, in macro or meso samples. The analysis of a trace level analyte or a micro sample requires a microanalytical balance.
Accuracy
For a macro sample that contains a major analyte, a relative error of 0.1– 0.2% is achieved routinely. The principal limitations are solubility losses, impurities in the precipitate, and the loss of precipitate during handling. When it is difficult to obtain a precipitate that is free from impurities, it often is possible to determine an empirical relationship between the precipitate’s mass and the mass of the analyte by an appropriate calibration.
Precision
The relative precision of precipitation gravimetry depends on the sample’s size and the precipitate’s mass. For a smaller amount of sample or precipitate, a relative precision of 1–2 ppt is obtained routinely. When working with larger amounts of sample or precipitate, the relative precision extends to several ppm. Few quantitative techniques can achieve this level of precision.
Sensitivity
For any precipitation gravimetric method we can write the following general equation to relate the signal (grams of precipitate) to the absolute amount of analyte in the sample
\[\text { g precipitate }=k \times \mathrm{g} \text { analyte } \label{8.13}\]
where k, the method’s sensitivity, is determined by the stoichiometry between the precipitate and the analyte.
Equation \ref{8.13} assumes we used a suitable blank to correct the signal for any contributions of the reagent to the precipitate’s mass.
Consider, for example, the determination of Fe as Fe2O3. Using a conservation of mass for iron, the precipitate’s mass is
\[\mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3}=\mathrm{g} \ \mathrm{Fe} \times \frac{1 \ \mathrm{mol} \ \mathrm{Fe}}{\text{AW Fe}} \times \frac{\text{FW Fe}_{2} \mathrm{O}_{3}}{2 \ \mathrm{mol} \ \mathrm{Fe}} \nonumber\]
and the value of k is
\[k=\frac{1}{2} \times \frac{\mathrm{FW} \ \mathrm{Fe}_{2} \mathrm{O}_{3}}{\mathrm{AW} \ \mathrm{Fe}} \label{8.14}\]
As we can see from Equation \ref{8.14}, there are two ways to improve a method’s sensitivity. The most obvious way to improve sensitivity is to increase the ratio of the precipitate’s molar mass to that of the analyte. In other words, it helps to form a precipitate with the largest possible formula weight. A less obvious way to improve a method’s sensitivity is indicated by the term of 1/2 in Equation \ref{8.14}, which accounts for the stoichiometry between the analyte and precipitate. We can also improve sensitivity by forming a precipitate that contains fewer units of the analyte.
Suppose you wish to determine the amount of iron in a sample. Which of the following compounds—FeO, Fe2O3, or Fe3O4—provides the greatest sensitivity?
- Answer
-
To determine which form has the greatest sensitivity, we use a conservation of mass for iron to find the relationship between the precipitate’s mass and the mass of iron.
\[\begin{aligned} \mathrm{g} \ \mathrm{FeO} &=\mathrm{g} \ \mathrm{Fe} \times \frac{1 \ \mathrm{mol} \ \mathrm{Fe}}{55.85 \ \mathrm{g} \ \mathrm{Fe}} \times \frac{71.84 \ \mathrm{g} \ \mathrm{FeO}}{\mathrm{mol} \ \mathrm{Fe}}=1.286 \times \mathrm{g} \ \mathrm{Fe} \\ \mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3} &=\mathrm{g} \ \mathrm{Fe} \times \frac{1 \ \mathrm{mol} \ \mathrm{Fe}}{55.85 \ \mathrm{g} \ \mathrm{Fe}} \times \frac{159.69 \ \mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3}}{2 \ \mathrm{mol} \ \mathrm{Fe}}=1.430 \times \mathrm{g} \ \mathrm{Fe} \\ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4} &=\mathrm{g} \ \mathrm{Fe} \times \frac{1 \ \mathrm{mol} \ \mathrm{Fe}}{55.85 \ \mathrm{g} \ \mathrm{Fe}} \times \frac{231.53 \ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4}}{3 \ \mathrm{mol} \ \mathrm{Fe}}=1.382 \times \mathrm{g} \ \mathrm{Fe} \end{aligned} \nonumber\]
Of the three choices, the greatest sensitivity is obtained with Fe2O3 because it provides the largest value for k.
Selectivity
Due to the chemical nature of the precipitation process, precipitants usually are not selective for a single analyte. For example, silver is not a selective precipitant for chloride because it also forms precipitates with bromide and with iodide. Interferents often are a serious problem and must be considered if accurate results are to be obtained.
Time, Cost, and Equipment
Precipitation gravimetry is time intensive and rarely practical if you have a large number of samples to analyze; however, because much of the time invested in precipitation gravimetry does not require an analyst’s immediate supervision, it is a practical alternative when working with only a few samples. Equipment needs are few—beakers, filtering devices, ovens or burners, and balances—inexpensive, routinely available in most laboratories, and easy to maintain.