7.9: Problems
- Page ID
- 162888
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. Because of the risk of lead poisoning, the exposure of children to lead-based paint is a significant public health concern. The first step in the quantitative analysis of lead in dried paint chips is to dissolve the sample. Corl evaluated several dissolution techniques [Corl, W. E. Spectroscopy 1991, 6(8), 40–43]. Samples of paint were collected and then pulverized using a Pyrex mortar and pestle. Replicate portions of the powdered paint were taken for analysis. The following table shows results for a paint sample and for a standard reference material. Both samples and standards were digested with HNO3 on a hot plate.
|
Replicate |
% w/w Pb in Sample |
% w/w Pb in Standard |
|---|---|---|
|
1 |
5.09 |
11.48 |
|
2 |
6.29 |
11.62 |
|
3 |
6.64 |
11.47 |
|
4 |
4.63 |
11.86 |
(a) Determine the overall variance, the variance due to the method and the variance due to sampling. (b) What percentage of the overall variance is due to sampling? (c) How might you decrease the variance due to sampling?
2. To analyze a shipment of 100 barrels of an organic solvent, you plan to collect a single sample from each of 10 barrels selected at random. From which barrels should you collect samples if the first barrel is given by the twelfth entry in the random number table in Appendix 14, with subsequent barrels given by every third entry? Assume that entries in the random number table are arranged by rows.
3. The concentration of dissolved O2 in a lake shows a daily cycle from the effect of photosynthesis, and a yearly cycle due to seasonal changes in temperature. Suggest an appropriate systematic sampling plan to monitor the daily change in dissolved O2. Suggest an appropriate systematic sampling plan for monitoring the yearly change in dissolved O2.
4. The data in the following table were collected during a preliminary study of the pH of an industrial wastewater stream.
| time (hr) | pH | time (hr) | pH |
|---|---|---|---|
|
0.5 |
4.4 | 9.0 | 5.7 |
|
1.0 |
4.8 | 9.5 | 5.5 |
| 1.5 | 5.2 | 10.0 | 6.5 |
| 2.0 | 5.2 | 10.5 | 6.0 |
| 2.5 | 5.6 | 11.0 | 5.8 |
| 3.0 | 5.4 | 11.5 | 6.0 |
| 3.5 | 5.4 | 12.0 | 5.6 |
| 4.0 | 4.4 | 12.5 | 5.6 |
| 4.5 | 4.8 | 13.0 | 5.4 |
| 5.0 | 4.8 | 13.5 | 4.9 |
| 5.5 | 4.2 | 14.0 | 5.2 |
| 6.0 | 4.2 | 14.5 | 4.4 |
| 6.5 | 3.8 | 15.0 | 4.0 |
| 7.0 | 4.0 | 15.5 | 4.5 |
| 7.5 | 4.0 0 | 16.0 | 4.0 |
| 8.0 | 3.9 | 16.5 | 5.0 |
| 8.5 | 4.7 | 17.0 | 5.0 |
Prepare a figure showing how the pH changes as a function of time and suggest an appropriate sampling frequency for a long-term monitoring program.
5. You have been asked to monitor the daily fluctuations in atmospheric ozone in the downtown area of a city to determine if there is relationship between daily traffic patterns and ozone levels. (a) Which of the following sampling plans will you use and why: random, systematic, judgmental, systematic–judgmental, or stratified? (b) Do you plan to collect and analyze a series of grab samples, or will you form a single composite sample? (c) Will your answers to these questions change if your goal is to determine if the average daily ozone level exceeds a threshold value? If yes, then what is your new sampling strategy?
6. The distinction between a homogeneous population and a heterogeneous population is important when we develop a sampling plan. (a) Define homogeneous and heterogeneous. (b) If you collect and analyze a single sample, can you determine if the population is homogeneous or is heterogeneous?
7. Beginning with equation 7.2.2, derive equation 7.2.3. Assume that the particles are spherical with a radius of r and a density of d.
8. The sampling constant for the radioisotope 24Na in homogenized human liver is approximately 35 g [Kratochvil, B.; Taylor, J. K. Anal. Chem. 1981, 53, 924A–938A]. (a) What is the expected relative standard deviation for sampling if we analyze 1.0-g samples? (b) How many 1.0-g samples must we analyze to obtain a maximum sampling error of ±5% at the 95% confidence level?
9. Engels and Ingamells reported the following results for the % w/w K2O in a mixture of amphibolite and orthoclase [Engels, J. C.; Ingamells, C. O. Geochim. Cosmochim. Acta 1970, 34, 1007–1017].
|
0.247 |
0.300 |
0.236 |
|
0.247 |
0.275 |
0.212 |
|
0.258 |
0.311 |
0.304 |
|
0.258 |
0.330 |
0.187 |
Each of the 12 samples had a nominal mass of 0.1 g. Using this data, calculate the approximate value for Ks, and then, using this value for Ks, determine the nominal mass of sample needed to achieve a percent relative standard deviation of 2%.
10. The following data was reported for the determination of KH2PO4 in a mixture of KH2PO4 and NaCl [Guy, R. D.; Ramaley, L.; Wentzell, P. D. J. Chem. Educ. 1998, 75, 1028–1033].
| nominal mass (g) | actual mass (g) | % w/w KH2PO4 |
|---|---|---|
| 0.10 | 0.1039 | 0.085 |
| 0.1015 | 1.078 | |
| 0.1012 | 0.413 | |
| 0.1010 | 1.248 | |
| 0.1060 | 0.654 | |
| 0.0997 | 0.507 | |
| 0.25 |
0.2515 |
0.847 |
|
0.2465 |
0.598 |
|
|
0.2770 |
0.431 |
|
|
0.2460 |
0.842 |
|
|
0.2485 |
0.964 |
|
|
0.2590 |
1.178 |
|
| 0.50 |
0.5084 |
1.009 |
|
0.4954 |
0.947 |
|
|
0.5286 |
0.618 |
|
|
0.5232 |
0.744 |
|
|
0.4965 |
0.572 |
|
|
0.4995 |
0.709 |
|
| 1.00 |
1.027 |
0.696 |
|
0.987 |
0.843 | |
|
0.991 |
0.535 | |
|
0.998 |
0.750 | |
|
0.997 |
0.711 | |
| 1.001 | 0.639 | |
| 2.50 | 2.496 | 0.766 |
| 2.504 | 0.769 | |
| 2.496 | 0.682 | |
| 2.496 | 0.609 | |
| 2.557 | 0.589 | |
| 2.509 | 0.617 |
(a) Prepare a graph of % w/w KH2PO4 vs. the actual sample mass. Is this graph consistent with your understanding of the factors that affect sampling variance. (b) For each nominal mass, calculate the percent relative standard deviation, Rexp, based on the data. The value of Ks for this analysis is estimated as 350. Use this value of Ks to determine the theoretical percent relative standard deviation, Rtheo, due to sampling. Considering these calculations, what is your conclusion about the importance of indeterminate sampling errors for this analysis? (c) For each nominal mass, convert Rtheo to an absolute standard deviation. Plot points on your graph that correspond to ±1 absolute standard deviations about the overall average % w/w KH2PO4 for all samples. Draw smooth curves through these two sets of points. Does the sample appear homogeneous on the scale at which it is sampled?
11.In this problem you will collect and analyze data to simulate the sampling process. Obtain a pack of M&M’s (or other similar candy). Collect a sample of five candies and count the number that are red (or any other color of your choice). Report the result of your analysis as % red. Return the candies to the bag, mix thoroughly, and repeat the analysis for a total of 20 determinations. Calculate the mean and the standard deviation for your data. Remove all candies from the bag and determine the true % red for the population. Sampling in this exercise should follow binomial statistics. Calculate the expected mean value and the expected standard deviation, and compare to your experimental results.
12. Determine the error (\(\alpha = 0.05\)) for the following situations. In each case assume that the variance for a single determination is 0.0025 and that the variance for collecting a single sample is 0.050. (a) Nine samples are collected, each analyzed once. (b) One sample is collected and analyzed nine times. (c) Five samples are collected, each analyzed twice.
13. Which of the sampling schemes in problem 12 is best if you wish to limit the overall error to less than ±0.30 and the cost to collect a single sample is $1 and the cost to analyze a single sample is $10? Which is the best sampling scheme if the cost to collect a single sample is $7 and the cost to analyze a single sample is $3?
14. Maw, Witry, and Emond evaluated a microwave digestion method for Hg against the standard open-vessel digestion method [Maw, R.; Witry, L.; Emond, T. Spectroscopy 1994, 9, 39–41]. The standard method requires a 2-hr digestion and is operator-intensive. The microwave digestion is complete in approximately 0.5 hr and requires little monitoring by the operator. Samples of baghouse dust from air-pollution-control equipment were collected from a hazardous waste incinerator and digested in triplicate before determining the concentration of Hg in ppm. Results are summarized in the following two tables.
| ppm Hg Following Microwave Digestion | |||
|---|---|---|---|
| sample | replicate 1 | replicate 2 | replicate 3 |
| 1 | 7.12 | 7.66 | 7.17 |
| 2 | 16.1 | 15.7 | 15.6 |
| 3 | 4.89 | 4.62 | 4.28 |
| 4 | 9.64 | 9.03 | 8.44 |
| a | 6.76 | 7.22 | 7.50 |
| 6 | 6.19 | 6.61 | 7.61 |
| 7 | 9.44 | 9.56 | 10.7 |
| 8 | 30.8 | 29.0 | 26.3 |
| ppm Hg Following Standard Digestion | |||
|---|---|---|---|
| sample | replicate 1 | replicate 2 | replicate 3 |
| 1 | 5.60 | 5.54 | 5.40 |
| 2 | 13.1 | 13.8 | 13.0 |
| 3 | 5.39 | 5.12 | 5.36 |
| 4 | 6.50 | 6.52 | 7.20 |
| a | 6.20 | 6.03 | 5.77 |
| 6 | 6.25 | 5.65 | 5.61 |
| 7 | 15.0 | 13.9 | 14.0 |
| 8 | 20.4 | 16.1 | 20.0 |
Does the microwave digestion method yields acceptable results when compared to the standard digestion method?
15. Simpson, Apte, and Batley investigated methods for preserving water samples collected from anoxic (O2-poor) environments that have high concentrations of dissolved sulfide [Simpson, S. L.: Apte, S. C.; Batley, G. E. Anal. Chem. 1998, 70, 4202–4205]. They found that preserving water samples with HNO3 (a common method for preserving aerobic samples) gave significant negative determinate errors when analyzing for Cu2+. Preserving samples by first adding H2O2 and then adding HNO3 eliminated the determinate error. Explain their observations.
16. In a particular analysis the selectivity coefficient, KA,I, is 0.816. When a standard sample with an analyte-to-interferent ratio of 5:1 is carried through the analysis, the error when determining the analyte is +6.3%. (a) Determine the apparent recovery for the analyte if RI =0. (b) Determine the apparent recovery for the interferent if RA = 0.
17. The amount of Co in an ore is determined using a procedure for which Fe in an interferent. To evaluate the procedure’s accuracy, a standard sample of ore known to have a Co/Fe ratio of 10.2 is analyzed. When pure samples of Co and Fe are taken through the procedure the following calibration relationships are obtained
\[S_{\mathrm{Co}}=0.786 \times m_{\mathrm{Co}} \text { and } S_{\mathrm{Fe}}=0.699 \times m_{\mathrm{Fe}} \nonumber\]
where S is the signal and m is the mass of Co or Fe. When 278.3 mg of Co are taken through the separation step, 275.9 mg are recovered. Only 3.6 mg of Fe are recovered when a 184.9 mg sample of Fe is carried through the separation step. Calculate (a) the recoveries for Co and Fe; (b) the separation factor; (c) the selectivity ratio; (d) the error if no attempt is made to separate the Co and Fe; (e) the error if the separation step is carried out; and (f ) the maximum possible recovery for Fe if the recovery for Co is 1.00 and the maximum allowed error is 0.05%.
18. The amount of calcium in a sample of urine is determined by a method for which magnesium is an interferent. The selectivity coefficient, KCa,Mg, for the method is 0.843. When a sample with a Mg/Ca ratio of 0.50 is carried through the procedure, an error of \(-3.7 \%\) is obtained. The error is +5.5% when using a sample with a Mg/Ca ratio of 2.0. (a) Determine the recoveries for Ca and Mg. (b) What is the expected error for a urine sample in which the Mg/Ca ratio is 10.0?
19. Using the formation constants in Appendix 12, show that F– is an effective masking agent for preventing a reaction between Al3+ and EDTA. Assume that the only significant forms of fluoride and EDTA are F– and Y4–.
20. Cyanide is frequently used as a masking agent for metal ions. Its effectiveness as a masking agent is better in more basic solutions. Explain the reason for this dependence on pH.
21. Explain how we can separate an aqueous sample that contains Cu2+, Sn4+, Pb2+, and Zn2+ into its component parts by adjusting the pH of the solution.
22. A solute, S, has a distribution ratio between water and ether of 7.5. Calculate the extraction efficiency if we extract a 50.0-mL aqueous sample of S using 50.0 mL of ether as (a) a single portion of 50.0 mL; (b) two portions, each of 25.0 mL; (c) four portions, each of 12.5 mL; and (d) five portions, each of 10.0 mL. Assume the solute is not involved in any secondary equilibria.
23. What volume of ether is needed to extract 99.9% of the solute in problem 23 when using (a) 1 extraction; (b) 2 extractions; (c) four extrac- tions; and (d) five extractions.
24. What is the minimum distribution ratio if 99% of the solute in a 50.0-mL sample is extracted using a single 50.0-mL portion of an organic solvent? Repeat for the case where two 25.0-mL portions of the organic solvent are used.
25. A weak acid, HA, with a Ka of \(1.0 \times 10^{-5}\) has a partition coefficient, KD, of \(1.2 \times 10^3\) between water and an organic solvent. What restriction on the sample’s pH is necessary to ensure that 99.9% of the weak acid in a 50.0-mL sample is extracted using a single 50.0-mL portion of the organic solvent?
26. For problem 25, how many extractions are needed if the sample’s pH cannot be decreased below 7.0?
27. A weak base, B, with a Kb of \(1.0 \times 10^{-3}\) has a partition coefficient, KD, of \(5.0 \times 10^2\) between water and an organic solvent. What restriction on the sample’s pH is necessary to ensure that 99.9% of the weak base in a 50.0-mL sample is extracted when using two 25.0-mL portions of the organic solvent?
28. A sample contains a weak acid analyte, HA, and a weak acid interferent, HB. The acid dissociation constants and the partition coefficients for the weak acids are Ka,HA = \(1.0 \times 10^{-3}\), Ka,HB = \(1.0 \times 10^{-7}\), KD,HA = KD,HB = \(5.0 \times 10^2\). (a) Calculate the extraction efficiency for HA and HB when a 50.0-mL sample, buffered to a pH of 7.0, is extracted using 50.0 mL of the organic solvent. (b) Which phase is enriched in the analyte? (c) What are the recoveries for the analyte and the interferent in this phase? (d) What is the separation factor? (e) A quantitative analysis is conducted on the phase enriched in analyte. What is the expected relative error if the selectivity coefficient, KHA,HB, is 0.500 and the initial ratio of HB/HA is 10.0?
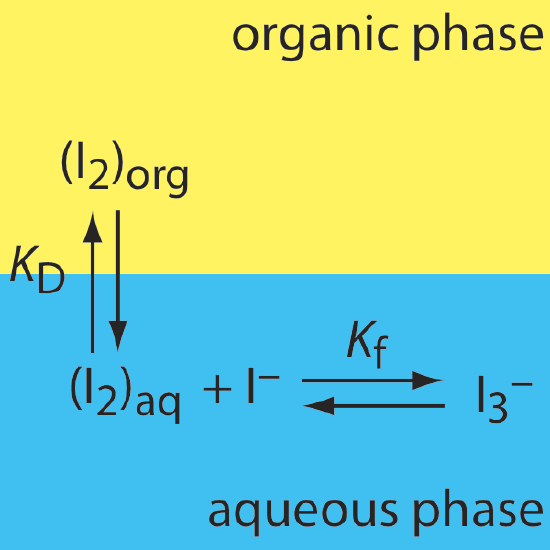
29. The relevant equilibria for the extraction of I2 from an aqueous solution of KI into an organic phase are shown below. (a) Is the extraction efficiency for I2 better at higher or at a lower concentrations of I–? (b) Derive an expression for the distribution ratio for this extraction.
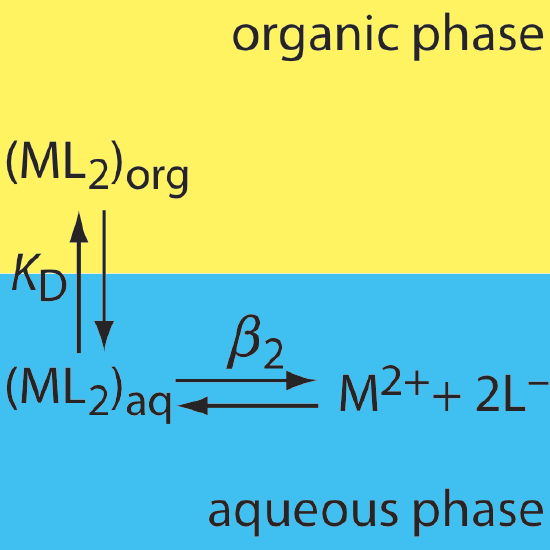
30. The relevant equilibria for the extraction of the metal-ligand complex ML2 from an aqueous solution into an organic phase are shown below. (a) Derive an expression for the distribution ratio for this extraction. (b) Calculate the extraction efficiency when a 50.0-mL aqueous sample that is 0.15 mM in M2+ and 0.12 M in L– is extracted using 25.0 mL of the organic phase. Assume that KD is 10.3 and that \(\beta_2\) is 560.
31. Derive equation 7.7.12 for the extraction scheme outlined in figure 7.7.5.
32. The following information is available for the extraction of Cu2+ by CCl4 and dithizone: KD,c = \(7 \times 10^4\); \(\beta_2 = 5 \times 10^{22}\); Ka,HL = \(3 \times 10^{-5}\); KD,HL = \(1.1 \times 10^4\); and n = 2. What is the extraction efficiency if a 100.0-mL sample of an aqueous solution that is \(1.0 \times 10^{-7}\) M Cu2+ and 1 M in HCl is extracted using 10.0 mL of CCl4 containing \(4.0 \times 10^{-4}\) M dithizone (HL)?
33. Cupferron is a ligand whose strong affinity for metal ions makes it useful as a chelating agent in liquid–liquid extractions. The following table provides pH-dependent distribution ratios for the extraction of Hg2+, Pb2+, and Zn2+ from an aqueous solution to an organic solvent.
| pH | Hg2+ | Pb2+ | Zn2+ |
|---|---|---|---|
| 1 | 3.3 | 0.0 | 0.0 |
| 2 | 10.0 | 0.43 | 0.0 |
| 3 | 32.3 | 999 | 0.0 |
| 4 | 32.3 | 9999 | 0.0 |
| 5 | 19.0 | 9999 | 0.18 |
| 6 | 4.0 | 9999 | 0.33 |
| 7 | 1.0 | 9999 | 0.82 |
| 8 | 0.54 | 9999 | 1.50 |
| 9 | 0.15 | 9999 | 2.57 |
| 10 | 0.05 | 9999 | 2.57 |
(a) Suppose you have a 50.0-mL sample of an aqueous solution that contains Hg2+, Pb2+, and Zn2+. Describe how you can separate these metal ions. (b) Under the conditions for your extraction of Hg2+, what percent of the Hg2+ remains in the aqueous phase after three 50.0-mL extractions with the organic solvent? (c) Under the conditions for your extraction of Pb2+, what is the minimum volume of organic solvent needed to extract 99.5% of the Pb2+ in a single extraction? (d) Under the conditions for your extraction of Zn2+, how many extractions are needed to remove 99.5% of the Zn2+ if each extraction uses 25.0 mL of organic solvent?


