2D NMR Basics
- Page ID
- 1803
Durations
The 2D NMR experiment belongs as well to the Fourier transform spectroscopy than to the impulsion one and relies on a sequence of three time intervals: preparation, evolution and detection (3). In some experiment another time interval is added before the detection: the mixing time ( Figure \(\PageIndex{1}\)).
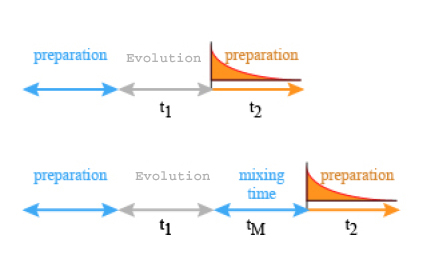
The preparation time
Upon the preparation time the spin system under study is firstly prepared, for example it is submitted either to a decoupling experiment or just to a transverse magnetization by the means of a 90° impulsion. It allows the excited nuclei to get back their equilibrium state between two successively executed pulse sequence (5)
The evolution time t1
During the evolution time \(t_1\), the spin system is evolving under the effect of different factors, each coherence evolves at its own characteristic frequency as a function of the chemical shift and of the scalar coupling of the corresponding nucleus.
The Mixing time
It is made of a pulse sequence which achieves coherence transfers in such a way that different frequencies can be correlated.
The detection time
The acquisition of the modulated signal takes place during the detection period. The sequence we just described does not constitute by itself a 2D NMR experiment.
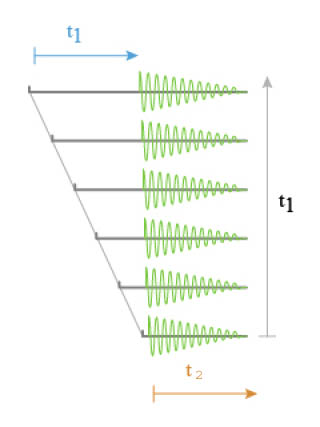
JEENER
The idea of Jeener consists in the stepwise increasing of the evolution time tl. This will allow to get an NMR signal under the aspect of a sampling of free precession signals of the s(t2) type. These FID will differ from each other only by the tl period duration written under a matricial form s(tl ,t2) (5). The tl delay is the time between the first and the second pulse ( Figure \(\PageIndex{2}\)).
The first Fourier transform as a function of tl gives us an interferogram of the form ![chap2_2_en_4[1].png](https://chem.libretexts.org/@api/deki/files/15318/chap2_2_en_4%255B1%255D.png?revision=1&size=bestfit&width=55&height=15) ( Figure \(\PageIndex{3}\)).
( Figure \(\PageIndex{3}\)).
![fig10[1].jpg](https://chem.libretexts.org/@api/deki/files/15317/fig10%255B1%255D.jpg?revision=1&size=bestfit&width=228&height=228)
A second Fourier transform, versus the second variable t2, gives an NMR spectrum with two frequencies dimensions F1 and F2 (Figure \(\PageIndex{3}\)). The result of this two fold Fourier transform does not get two spectra ![chap2_2_en_5[1].png](https://chem.libretexts.org/@api/deki/files/15319/chap2_2_en_5%255B1%255D.png?revision=1&size=bestfit&width=39&height=15) and
and ![chap2_2_en_6[1].png](https://chem.libretexts.org/@api/deki/files/15320/chap2_2_en_6%255B1%255D.png?revision=1&size=bestfit&width=39&height=15) but only one spectrum as a function of two independent frequencies, exhibiting a peak with the coordinates
but only one spectrum as a function of two independent frequencies, exhibiting a peak with the coordinates ![chap2_2_en_7[1].png](https://chem.libretexts.org/@api/deki/files/15321/chap2_2_en_7%255B1%255D.png?revision=1&size=bestfit&width=58&height=15) . Thus, an alimentation evolving with the frequency
. Thus, an alimentation evolving with the frequency ![chap2_2_en_8[1].png](https://chem.libretexts.org/@api/deki/files/15322/chap2_2_en_8%255B1%255D.png?revision=1&size=bestfit&width=18&height=15) in the time course t1 has been converted in another coherence evolving with the frequency
in the time course t1 has been converted in another coherence evolving with the frequency ![chap2_2_en_9[1].png](https://chem.libretexts.org/@api/deki/files/15323/chap2_2_en_9%255B1%255D.png?revision=1&size=bestfit&width=22&height=12) during the period t2.
during the period t2.
![fig11[1].jpg](https://chem.libretexts.org/@api/deki/files/15325/fig11%255B1%255D.jpg?revision=1&size=bestfit&width=297&height=297)
This double Fourier transform in both dimension yields thus a matrix ![chap2_2_en_10[1].png](https://chem.libretexts.org/@api/deki/files/15326/chap2_2_en_10%255B1%255D.png?revision=1&size=bestfit&width=62&height=15) . ( Figure \(\PageIndex{3}\) ).
. ( Figure \(\PageIndex{3}\) ).

