9.3: Pressure
- Page ID
- 49342
You are probably familiar with the general idea of pressure from experiences in pumping tires or squeezing balloons. A gas exerts force on any surface that it contacts. The force per unit surface area is called the pressure and is represented by P. The symbols F and A represent force and area, respectively. On the image below, a force is pushing down on the circular area of a barometer. The pressure is then the amount of force pushing on a unit area of the circle of the barometer.
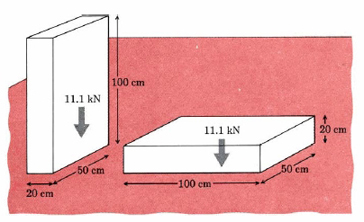
\[\text{Pressure}=\frac{\text{force}}{\text{area}}\text{ }P=\frac{F}{A} \nonumber \] As a simple example of pressure, consider a rectangular block of lead which measures 20.0 cm by 50.0 cm by 100.0 cm (Figure \(\PageIndex{1}\) ). The volume V of the block is 1.00 × 105 cm3, and since the density ρ of Pb is 11.35 g cm–3, the mass m is
\[m=V\rho =\text{1}\text{.00 }\times \text{ 10}^{\text{5}}\text{ cm}^{\text{3}}\text{ }\times \text{ }\frac{\text{11}\text{.35 g}}{\text{1 cm}^{\text{3}}}\text{ }\label{1} =\text{1}\text{.135 }\times \text{ 10}^{\text{6}}\text{ g}=\text{1}\text{.135 }\times \text{ 10}^{\text{3}}\text{ kg} \]
According to the second law of motion, discovered by British physicist Isaac Newton, the force on an object is the product of the mass of the object and its acceleration a:
\[F = ma\label{4} \]
At the surface of the earth, the acceleration of gravity is 9.81 m s–2. Substituting the mass of the lead block into Eq. \(\ref{4}\), we have
\[F = 1.135 \times 10^{3} \text{ kg} \times \text{ m }\text{s}^{\text{-2}} = 11.13 \times 10 \text{ kg} \text{ m}\text{ s}^\text{-2} \nonumber \] The units kilogram meter per square second are given the name newton in the International System and abbreviated N. Thus the force which gravity exerts on the lead block (the weight of the block) is 11.13 × 103 N. A block that is resting on the floor will always exert a downward force of 11.13 kN. The pressure exerted on the floor depends on the area over which this force is exerted. If the block rests on the 20.0 cm by 50.0 cm side (Figure 9.2a), its weight is distributed over an area of 20.0 cm × 50.0 cm = 1000 cm3. Thus:
\[P=\frac{F}{A}=\frac{\text{11}\text{.13 kN}}{\text{1000 cm}^{\text{2}}}=\frac{\text{11}\text{.13 kN}}{\text{1000 cm}^{\text{2}}}\text{ }\times \text{ }\left( \frac{\text{100 cm}}{\text{1 m}} \right)^{\text{2}} =\frac{\text{11}\text{.13 kN}}{\text{10}^{\text{3}}\text{ cm}^{\text{2}}}=\frac{\text{10}^{\text{4}}\text{ cm}^{\text{2}}}{\text{1 m}^{\text{2}}}=\text{111}\text{.3 }\frac{\text{kN}}{\text{m}^{\text{2}}} =\text{111}\text{.3 }\times \text{ 10}^{\text{3}}\text{ N m}^{-\text{2}} \nonumber \]
Thus we see that pressure can be measured in units of newtons (force) per square meter (area). The units newton per square meter are used in the International System to measure pressure, and they are given the name pascal (abbreviated Pa). Like the newton, the pascal honors a famous scientist, in this case Blaise Pascal (1623 to 1662), one of the earliest investigators of the pressure of liquids and gases.
If the lead block is laid on its side (Figure 1b), the pressure is altered. The area of contact with the floor is now 50.0 cm × 100.0 cm = 5000 cm2, and so
\[P=\frac{F}{A}=\frac{\text{11}\text{.13 }\times \text{ 10}^{\text{3}}\text{ N}}{\text{5000 cm}^{\text{2}}}=\frac{\text{11}\text{.13 }\times \text{ 10}^{\text{3}}\text{ N}}{\text{0}\text{.500 m}^{\text{2}}} =\text{22}\text{.26 }\times \text{ 10}^{\text{3}}\text{ N m}^{-\text{2}}=\text{22}\text{.26 kPa} \nonumber \] When the block is lying flat, its pressure on the floor (22.26 kPa) is only one-fifth as great as the pressure (111.3 kPa) when it stands on end. This is because the area of contact is 5 times larger.
The air surrounding the earth is pulled toward the surface by gravity in the same way as the lead block we have been discussing. Consequently the air also exerts a pressure on the surface. This is called atmospheric pressure.
The following video shows the "power" of atmospheric pressure. A metal can full of water is heated until the water inside boils, creating a high internal pressure. The can is the put upside down into a bowl of cold ice water, causing the formerly hot water vapor to cool and decrease in volume. This cooling causes a decrease in the internal pressure of the can. The lower pressure exerts less force on the can and can no longer counter the atmospheric pressure coming from the outside of the can, which pushes inward, crushing the can.
Because winds may add more air or take some away from the vertical column above a given area on the surface, atmospheric pressure will vary above and below the result obtained in Example 9.1. Pressure also decreases as one moves to higher altitudes. The tops of the Himalayas, the highest mountains in the world at about 8000 m (almost 5 miles), are above more than half the atmosphere. The lower pressure at such heights makes breathing very difficult—even the slightest exertion leaves one panting and weak. For this reason jet aircraft, which routinely fly at altitudes of 8 to 10 km, have equipment to maintain air pressure in their cabins artificially.
It is often convenient to express pressure using a unit which is about the same as the average atmospheric pressure at sea level. As we saw in Example 1, atmospheric pressure is about 101 kPa, and the standard atmosphere (abbreviated atm) is defined as exactly 101.325 kPa. Since this unit is often used, it is useful to remember that
\[1 \text{ atm} = 101.325 \text{ kPa} \nonumber \]
The total mass of air directly above a 30 cm by 140 cm section of the Atlantic Ocean was 4.34 × 103 kg on July 27, 1977. Calculate the pressure exerted on the surface of the water by the atmosphere.
Solution First calculate the force of gravitational attraction on the air:
\[F = ma = 4.34 \times 10^{3} \text{ kg} \times 9.81 \text{ m }\text{s}^{\text{-2}} = 4.26 \times 10^{4} \text{ kg m s}^\text{-2} = 4.26 \times 10^{4} \text{ N} \nonumber \] The area is\[A=\text{30 cm }\times \text{ 140 cm}=\text{4200 cm}^{\text{2}}\text{ }\times \text{ }\left( \frac{\text{1 m}}{\text{100 cm}} \right)^{\text{2}}\text{ }=\text{0}\text{.42 m}^{\text{2}} \nonumber \]
Thus the pressure is \[P=\frac{F}{A}=\frac{\text{4}\text{.26 }\times \text{ 10}^{\text{4}}\text{ N}}{\text{0}\text{.42 m}^{\text{2}}}=\text{1}\text{.01 }\times \text{ 10}^{\text{5}}\text{ Pa}=\text{101 kPa} \nonumber \]

