The Cell Potential

The batteries in your remote and the engine in your car are only a couple of examples of how chemical reactions create power through the flow of electrons. The cell potential is the way in which we can measure how much voltage exists between the two half cells of a battery. We will explain how this is done and what components allow us to find the voltage that exists in an electrochemical cell.

Introduction

The cell potential, \(E_{cell}\), is the measure of the potential difference between two half cells in an electrochemical cell. The potential difference is caused by the ability of electrons to flow from one half cell to the other. Electrons are able to move between electrodes because the chemical reaction is a redox reaction. A redox reaction occurs when a certain substance is oxidized, while another is reduced. During oxidation, the substance loses one or more electrons, and thus becomes positively charged. Conversely, during reduction, the substance gains electrons and becomes negatively charged. This relates to the measurement of the cell potential because the difference between the potential for the reducing agent to become oxidized and the oxidizing agent to become reduced will determine the cell potential. The cell potential (E_cell) is measured in voltage (V), which allows us to give a certain value to the cell potential.

Electrochemical Cell

An electrochemical cell is comprised of two half cells. In one half cell, the oxidation of a metal electrode occurs, and in the other half cell, the reduction of metal ions in solution occurs. The half cell essentially consists of a metal electrode of a certain metal submerged in an aqueous solution of the same metal ions. The electrode is connected to the other half cell, which contains an electrode of some metal submerged in an aqueous solution of subsequent metal ions. The first half cell, in this case, will be marked as the anode. In this half cell, the metal in atoms in the electrode become oxidized and join the other metal ions in the aqueous solution. An example of this would be a copper electrode, in which the Cu atoms in the electrode loses two electrons and becomes Cu²⁺ .

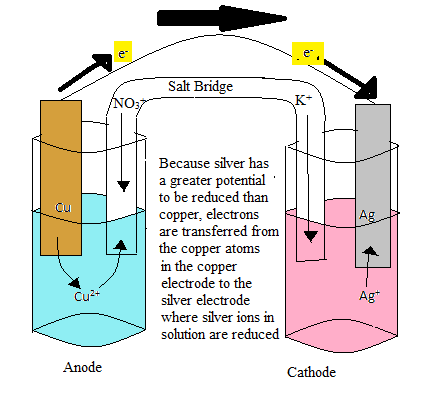
The Cu²⁺ ions would then join the aqueous solution that already has a certain molarity of Cu²⁺ ions. The electrons lost by the Cu atoms in the electrode are then transferred to the second half cell, which will be the cathode. In this example, we will assume that the second half cell consists of a silver electrode in an aqueous solution of silver ions. As the electrons are passed to the Ag electrode, the Ag⁺ ions in solution will become reduced and become an Ag atom on the Ag electrode. In order to balance the charge on both sides of the cell, the half cells are connected by a salt bridge. As the anode half cell becomes overwhelmed with Cu²⁺ ions, the negative anion of the salt will enter the solution and stabilized the charge. Similarly, in the cathode half cell, as the solution becomes more negatively charged, cations from the salt bridge will stabilize the charge.

How does this relate to the cell potential?

For electrons to be transferred from the anode to the cathode, there must be some sort of energy potential that makes this phenomenon favorable. The potential energy that drives the redox reactions involved in electrochemical cells is the potential for the anode to become oxidized and the potential for the cathode to become reduced. The electrons involved in these cells will fall from the anode, which has a higher potential to become oxidized to the cathode, which has a lower potential to become oxidized. This is analogous to a rock falling from a cliff in which the rock will fall from a higher potential energy to a lower potential energy.

Note

The difference between the anode's potential to become reduced and the cathode's potential to become reduced is the cell potential.

\[E^o_{Cell}= E^o_{Red,Cathode} - E^o_{Red,Anode} \nonumber \]

Note:

• Both potentials used in this equation are standard reduction potentials, which are typically what you find in tables (e.g., Table P1 and Table P2). However, the reaction at the anode is actually an oxidation reaction -- the reverse of a reduction reaction. This explains the minus sign. We would have used a plus sign had we been given an oxidation potential \(E^o_{Ox,Anode}\) instead, since \(E^o_{Red}=E^o_{Ox}\).
• The superscript "o" in E^o indicates that these potentials are correct only when concentrations are 1 M and pressures are 1 bar. A correction called the "Nernst Equation" must be applied if conditions are different.

Electrochemical cell

Here is the list of the all the components:

1. Two half cells
2. Two metal electrodes
3. One voltmeter
4. One salt bridge
5. Two aqueous solutions for each half cell

All of these components create the Electrochemical Cell.

How to measure the cell potential?

The image above is an electrochemical cell. The voltmeter at the very top in the gold color is what measures the cell voltage, or the amount of energy being produced by the electrodes. This reading from the voltmeter is called the voltage of the electrochemical cell. This can also be called the potential difference between the half cells, E_cell. Volts are the amount of energy for each electrical charge; 1V=1J/C: V= voltage, J=joules, C=coulomb. The voltage is basically what propels the electrons to move. If there is a high voltage, that means there is high movement of electrons. The voltmeter reads the transfer of electrons from the anode to the cathode in Joules per Coulomb.

Cell Diagram

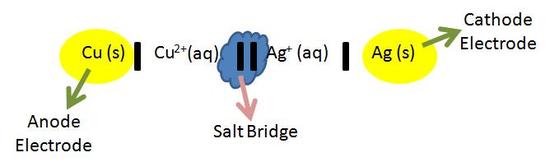
The image above is called the cell diagram. The cell diagram is a representation of the overall reaction in the electrochemical cell. The chemicals involved are what are actually reacting during the reduction and oxidation reactions. (The spectator ions are left out). In the cell diagram, the anode half cell is always written on the left side of the diagram, and in the cathode half cell is always written on the right side of the diagram. Both the anode and cathode are seperated by two vertical lines (ll) as seen in the blue cloud above. The electrodes (yellow circles) of both the anode and cathode solutions are seperated by a single vertical line (l). When there are more chemicals involved in the aqueous solution, they are added to the diagram by adding a comma and then the chemical. For example, in the image above, if copper wasn't being oxidized alone, and another chemical like K was involved, you would denote it as (Cu, K) in the diagram. The cell diagram makes it easier to see what is being oxidized and what is being reduced. These are the reactions that create the cell potential.

Standard Cell Potential

The standard cell potential (\(E^o_{cell}\)) is the difference of the two electrodes, which forms the voltage of that cell. To find the difference of the two half cells, the following equation is used:

\[E^o_{Cell}= E^o_{Red,Cathode} - E^o_{Red,Anode} \tag{1a} \]

with

• \(E^o_{Cell}\) is the standard cell potential (under 1M, 1 Barr and 298 K).
• \(E^o_{Red,Cathode}\) is the standard reduction potential for the reduction half reaction occurring at the cathode
• \(E^o_{Red,Anode}\) is the standard reduction potential for the oxidation half reaction occurring at the anode

The units of the potentials are typically measured in volts (V). Note that this equation can also be written as a sum rather than a difference

\[E^o_{Cell}= E^o_{Red,Cathode} + E^o_{Ox,Anode} \tag{1b} \]

where we have switched our strategy from taking the difference between two reduction potentials (which are traditionally what one finds in reference tables) to taking the sum of the oxidation potential and the reduction potential (which are the reactions that actually occur). Since E^o_{Red}=-E^o_{Ox}, the two approaches are equivalent.

Standard Cell Potential Example

The example will be using the picture of the Copper and Silver cell diagram. The oxidation half cell of the redox equation is:

Cu(s) → Cu²⁺(aq) + 2e^- E^o_Ox= -0.340 V

where we have negated the reduction potential E^o_Red= 0.340 V, which is the quantity we found from a list of standard reduction potentials, to find the oxidation potential E^o_Ox. The reduction half cell is:

( Ag⁺ + e^- → Ag(s) ) x2 E^o_Red= 0.800 V

where we have multiplied the reduction chemical equation by two in order to balance the electron count but we have not doubled E^o_Red since E^o values are given in units of voltage. Voltage is energy per charge, not energy per reaction, so it does not need to account for the number of reactions required to produce or consume the quantity of charge you are using to balance the equation. The chemical equations can be summed to find:

Cu(s) + 2Ag⁺ + 2e^- → Cu²⁺(aq) + 2Ag(s) + 2e^-

and simplified to find the overall reaction:

Cu(s) + 2Ag⁺ → Cu²⁺(aq) + 2Ag(s)

where the potentials of the half-cell reactions can be summed

E^o_Cell= E^o_Red,Cathode+E^o_Ox,Anode

E^o_Cell = 0.800 V + (^-0.340 V)

E^o_Cell = 0.460V

to find that the standard cell potential of this cell is 0.460 V. We are done.

Note that since E^o_{Red}=-E^o_{Ox} we could have accomplished the same thing by taking the difference of the reduction potentials, where the absent or doubled negation accounts for the fact that the reverse of the reduction reaction is what actually occurs.

E^o_Cell= E^o_Red,Cathode-E^o_Red,Anode

E^o_Cell = 0.800V - 0.340V

E^o_Cell = 0.460V

Important Standard Electrode (Reduction) Potentials

The table below is a list of important standard electrode potentials in the reduction state. To determine oxidation electrodes, the reduction equation can simply be flipped and its potential changed from positive to negative (and vice versa). When using the half cells below, instead of changing the potential the equation below can be used without changing any of the potentials from positive to negative (and vice versa):

E^o_Cell= E^o_Red,Cathode - E^o_Red,Anode

Table: Reduction Half-Reaction Eo, V

Acidic Solution
F2(g) + 2e^- → 2 F^-(aq)	+2.866
O3(g) + 2H^+(aq) + 2e^-→ O2(g) + H2O(l)	+2.075
S2O8^2^-(aq) + 2e^- → 2SO4^2^-(aq)	+2.01
H2O2(aq) + 2H^+(aq) +2e^- → 2H2O(l)	+1.763
MnO4^-(aq) + 8H^+(aq) + 5e^- → Mn^2^+(aq) + 4H2O(l)	+1.51
PbO2(s) + 4H^+(aq) + 2e^- → Pb^2^+(aq) + 4H2O(l)	+1.455
Cl2(g) + 2e^- → 2Cl^-(aq)	+1.358
Cr2O7^2^-(aq) + 14H^+(aq) + 6e^- → 2Cr^3^+(aq) + 7H2O(l)	+1.33
MnO2(s) + 4H^+(aq) +2e^- -> Mn^2^+(aq) + 2H2O(l)	+1.23
O2(g) + 4H^+(aq) + 4e^- → 2H2O(l)	+1.229
2IO3^-(aq) + 12H^+(aq) + 10e^- → I2(s) + 6H2O(l)	+1.20
Br2(l) + 2e^- → 2Br^-(aq)	+1.065
NO3^-(aq) + 4H^+(aq) + 3e^- → NO(g) + 2 H2O(l)	+0.956
Ag^+(aq) + e^- → Ag(s)	+0.800
Fe^3^+(aq) + e^- → Fe^2^+(aq)	+0.771
O2(g) + 2H^+(ag) + 2e^- → H2O2(aq)	+0.695
I2(s) + 2e^- → 2I^-(aq)	+0.535
Cu^2^+(aq) + 2e^- → Cu(s)	+0.340
SO4^2^-(aq) + 4H^+(aq) + 2e^- → 2H2O(l) + SO2(g)	+0.17
Sn^4^+(aq) + 2e^- → Sn^2^+(aq)	+0.154
S(s) + 2H^+(aq) + 2e^- → H2S(g)	+0.14
2H^+(aq) + 2e^- → H2(g)	0
Pb^2^+(aq) + 2e^- → Pb	-0.125
Sn^2^+(aq) + 2e^- → Sn(s)	-0.137
Fe^2^+(aq) + 2e^- → Fe(s)	-0.440
Zn^2^+ + 2e^- → Zn(s)	-0.763
Al^3^+(aq) + 3e^- → Al(s)	-1.676
Mg^2^+(aq) + 2e^- → Mg(s)	-2.356
Na^+(aq) + e^- → Na(s)	-2.713
Ca^2^+(aq) + 2e^- → Ca(s)	-2.84
K^+(aq) + e^- → K(s)	-2.924
Li^+(aq) + e^- → Li(s)	-3.040
Basic Solution
O3(aq) + H2O(l) + 2e^- → O2(g) + 2OH^-(aq)	+1.246
OCl^-(aq) + H2O(l) + 2e^- → Cl^-(aq) + 2OH^-(aq)	+0.890
O2(g) + 2H2O(l) +4e^- → 4OH^-(aq)	+0.401
2H2O(l) + + 2e^- → H2(aq) + 2OH^-(aq)	-0.0828

Problems

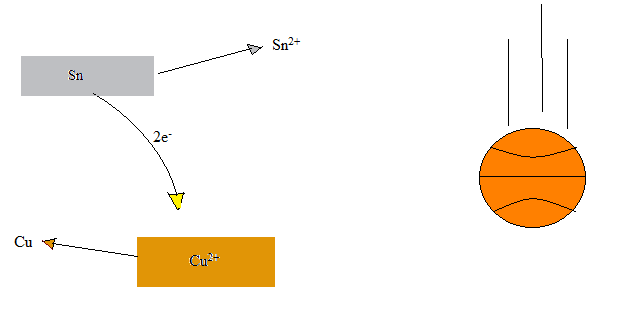
1. For this redox reaction \[Sn(s) + Pb^{2+}(aq) \rightarrow Sn^{2+}(aq) + Pb (s) \nonumber \] write out the oxidation and reduction half reactions. Create a cell diagram to match your equations.
2. From the image above, of the cell diagram, write the overall equation for the reaction.
3. If \(Cu^{2+}\) ions in solution around a \(Cu\) metal electrode is the cathode of a cell, and \(K^+\) ions in solution around a K metal electrode is the anode of a cell, which half cell has a higher potential to be reduced?
4. What type of reaction provides the basis for a cell potential?
5. How is the cell potential measured and with what device is it measured?
6. The \(E^o_{cell}\) for the equation \[ 4Al(s) + 3O_2(g) + 6H_2O(l) + 4OH^-(aq) \rightarrow 4[Al(OH)_4]^-(aq) \nonumber \] is +2.71 V. If the reduction of \(O_2\) in \(OH^-\) is +0.401 V. What is the reduction half-reaction for this reduction half reaction? \[[Al(OH)_4]^-(aq) + 3e^- \rightarrow Al(s) + 4OH^- \nonumber \]

Answers

1. oxidation: Sn_(s) → Sn²⁺_(aq) + 2e^-_(aq)
   reduction: Pb²⁺_(aq) + 2e^-_(aq) → Pb_(s)
   cell diagram: Sn_(s) | Sn²⁺_(aq) || Pb²⁺_(aq) | Pb_(s)
2. Cu_(s) + 2Ag⁺_(aq) → 2Ag_(s) + Cu²⁺_(aq)
3. Because the half cell containing the \(Cu\) electrode in \(Cu^{2+}\) solution is the cathode, this is the half cell where reduction is taking place. Therefore, this half cell has a higher potential to be reduced.
4. The redox reaction.
5. Cell potential is measured in Volts (=J/C). This can be measured with the use of a voltmeter.
6. We can divide the net cell equation into two half-equations.

• Oxidation: {Al(s) + 4OH^-(aq) → [Al(OH₄)]^-(aq) + 3e^-} x4; -E^o= ? This is what we are solving for.
• Reduction: {O₂(g) + 2H₂O(l) + 4e^- → 4OH^-(aq)} x3 E^o= +0.401V
• Net: 4Al(s) + 3O₂(g) + 6H₂O(l) + 4OH^-(aq) → 4[Al(OH)₄]^-(aq) E^o_cell = 2.71V

E^o_cell= 2.71V= +0.401V - E^o{Al(OH)₄]^-(aq)/Al(s)}

E^o{[Al(OH)₄]^-(aq)/Al(s)} = 0.401V - 2.71V = -2.31V

Confirm this on the table of standard reduction potentials

References

1. Petrucci, Harwood, Herring, and Madura. General Chemistry: Principles and Modern Applications. 9th ed. Upper Saddle River, New Jersey: Pearson Education, 2007.

Contributors and Attributions

• Katherine Barrett, Gianna Navarro, Joseph Koressel, Justin Kohn