Connection between Cell Potential, ∆G, and K

Learning Objectives

The connection between cell potential, Gibbs energy and constant equilibrium are directly related in the following multi-part equation:

$$\Delta G^o= -RT\ln K_{eq} = -nFE^o_{cell} \nonumber$$

∆G: Gibbs Energy

∆G is the change of Gibbs (free) energy for a system and ∆G° is the Gibbs energy change for a system under standard conditions (1 atm, 298K). On an energy diagram, ∆G can be represented as:

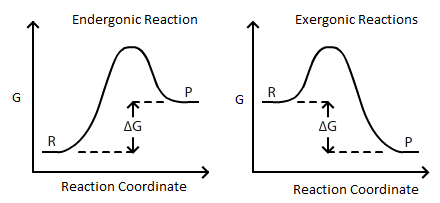
Where ∆G is the difference in the energy between reactants and products. In addition ∆G is unaffected by external factors that change the kinetics of the reaction. For example if E_a(activation energy) were to decrease in the presence of a catalyst or the kinetic energy of molecules increases due to a rise in temperature, the ∆G value would remain the same.

E°_cell: Standard Cell Potential

E°_cell is the electromotive force (also called cell voltage or cell potential) between two half-cells. The greater the E°_cell of a reaction the greater the driving force of electrons through the system, the more likely the reaction will proceed (more spontaneous). E°_cell is measured in volts (V). The overall voltage of the cell = the half-cell potential of the reduction reaction + the half-cell potential of the oxidation reaction. To simplify,

$$E^o_{cell} = E^o_{reduction} - E^o_{oxidation} \label{1}$$

or

$$E^o_{cell} = E^o_{cathode} - E^o_{anode} \label{2}$$

The potential of an oxidation reduction (loss of electron) is the negative of the potential for a reduction potential (gain of electron). Most tables only record the standard reduction half-reactions as standard reduction potentials. To find the standard oxidation potential, simply reverse the sign of the standard reduction potential.

Note

The more positive reduction potential of reduction reactions are more spontaneous. When viewing a cell reduction potential table, the higher the cell is on the table, the higher potential it has as an oxidizing agent.

Difference between E_cell and Eº_cell

Eº cell is the standard state cell potential, which means that the value was determined under standard states. The standard states include a concentration of 1 Molar (mole per liter) and an atmospheric pressure of 1. Similar to the standard state cell potential, Eº_cell, the E_cell is the non-standard state cell potential, which means that it is not determined under a concentration of 1 M and pressure of 1 atm. The two are closely related in the sense that the standard cell potential is used to calculate for the cell potential in many cases.

$$E_{cell}= E^o_{cell} -\dfrac{RT}{nF} \ln\; Q \label{3}$$

Other simplified forms of the equation that we typically see:

$$E_{cell}= E^o_{cell} -\dfrac{0.0257}{n} \ln \; Q \label{4}$$

or in terms of $\log_{10}$ (base 10) instead of the natural logarithm (base e)

$$E_{cell}= E^o_{cell} - \dfrac{0.0592}{n} \log_{10}\; Q \label{5}$$

Both equations applies when the temperature is 25ºC. Deviations from 25ºC requires the use of the original equation. Essentially, Eº is E at standard conditions

Example 1

What is the value of $E_{cell}$ for the voltaic cell below:

$$\ce{Pt(s)} | \ce{Fe^{2+}}(0.1\, M), \ce{Fe^{3+}}(0.2\, M) || \ce{Ag^{+}} (0.1\, M)| \ce{Ag(s)} \nonumber$$

Solution

To use the Nernst equation, we need to establish $E^o_{cell}$ and the reaction to which the cell diagram corresponds so that the form of the reaction quotient (Q) can be revealed. Once we have determined the form of the Nernst equation, we can insert the concentration of the species.

Solve:

$$\begin{align*} E^o_{cell} &= E^o_{SRP}(cathode - E^o_{SRP}(anode)\\[4pt] &= E^o(Ag^{+}/Ag) - E^o(Fe^{3+}/Fe^{2+}) \\[4pt] &= 0.800\,V - 0.771\,V \\[4pt] &= 0.029\, V \end{align*}$$

Now to determine $E_{cell}$ for the reaction

$$\ce{Fe^{2+}}(0.1\,M) + \ce{Ag^{+}}(1.0\,M) → \ce{Fe^{3+}}(0.20\,M) + \ce{Ag(s)} \nonumber$$

Use the Nernst equation

$$\begin{align*} E_{cell} &= 0.029\,V - \left(\dfrac{0.0592\,V}{1}\right) \log \dfrac{[Fe^{3+}]}{[Fe^{2+}][Ag]} \\[4pt] &=0.029\,V - 0.0592\,V \log \dfrac{0.2}{(0.1)(0.1)} \\[4pt] &=-0.048\,V \end{align*}$$

Note that this reaction is spontaneous (positive $E_{cell}$) as written under standard conditions, but is non-spontaneous (negative $E_{cell}$) under the non-standard conditions of question.

K: The Equilibrium Constant

$K$ is the equilibrium constant of a general reaction

$$aA + bB \leftrightharpoons cC + dD \label{6}$$

and is expressed by the reaction quotient:

$$K_c= \dfrac{[C]^c[D]^d}{[A]^a[B]^b} \label{7}$$

Example 2

Given $K = 2.81 \times 10^{-16}$ for a following reaction

$$\ce{Cu^{2+}(aq) + Ag(s) \rightleftharpoons Cu(s) + 2Ag^{+}} \nonumber$$

Find ∆G.

Solution

Use the following formula:

$$\begin{align*} ∆G &=-RT\ln K \\[4pt] &= (8.314) (298\,K) \ln (2.81 \times 10^{-16}) \\[4pt] &= -8.87 \times 10^5 J/mole \\[4pt] &= 8.871 \,kJ/mol \end{align*}$$

The Relationship Between the Three

The relationship between $∆G$, $K$, and $E^°_{cell}$ can be represented by the following diagram.

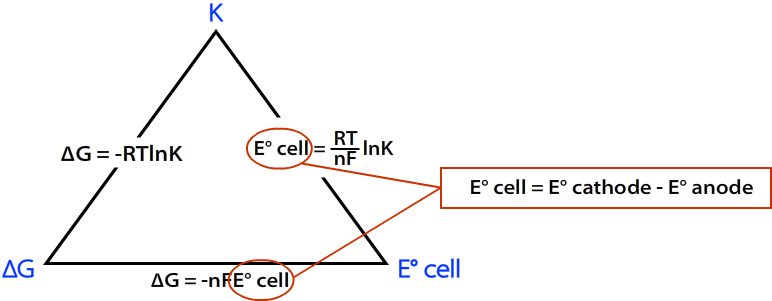
where

• R = 8.314 J mol C^-1
• T = Temp in K
• n = moles of e^- from balanced redox reaction
• F = Faraday's constant = 96,485 C/mol

$E^o_{cell}$ can be calculated using the following formula:

$$E^o_{cell} = E^o_{cathode} – E^o_{anode} = E^o_{Reduction} – E^o_{Oxidation} \label{8}$$

Summary Table

Eo cell	$\Delta G$	Q & K Relationship	Reaction Direction	Spontaneity (as written)
>0	-	Q<K	Forward	Spontaneous
<0	+	Q>K	Backward	Non-spontaneous
=0	=0	Q=K	No Reaction	N/A

Example 3: Using ∆G=-RT lnK

Find the $E^o_{cell}$ for the following coupled half-reactions

Solution

1. Determine the cathode and anode in the reaction

$$\ce{Zn(s) <=> Zn^{2+}(aq) + 2e^{-}} \nonumber$$

Anode, Oxidation half-reaction (since $\ce{Zn(s)}$ increase oxidation state from 0 to +2)

$$\ce{Cu^{2+}(aq) + 2e^{-} <=> Cu(s)} \nonumber$$

Cathode, Reduction half-rection (since $\ce{Cu^{2+}(aq)}$ decreases oxidation state from +2 to 0)

2. Determine the $E^o_{cell}$ values using the standard reduction potential table (Table P1)

$$\ce{Zn(s) <=> Zn^{2+}(aq) + 2e^{-}} \quad\quad E_{SRP} = -0.763 \nonumber$$

$$\ce{Cu^{2+}(aq) + 2e^{-} <=> Cu(s)} \quad\quad E_{SRP}=+0.340 \nonumber$$

3. Use

$$\begin{align*} E^°_{cell} &= E^°_{SRP}(\text{cathode}) - E^o_{SRP}(\text{anode}) \\[4pt] &= 0.340 \,V - (-0.763\, V) \\[4pt] &= 1.103\, V \end{align*}$$

Example 4: Gibbs Energy Difference

Find ∆G for the following reaction:

$$\ce{2Al(s) + 3Br2(l) <=> 2Al^{3+}}(aq, 1.0\,M) + \ce{6Br^{-}}(aq, 1.0\,M) \nonumber$$

Solution

Step 1: Separate the reaction into its two half reactions

$$\ce{2Al(s) <=> 2Al^{3+}(aq)} \nonumber$$

$$\ce{3Br2(l) <=> 6Br^{-}(aq, 1\,M)} \nonumber$$

Step 2: Balance the half equations using O, H, and charge using e-

2Al_(s) ↔ 2Al^3+(aq) +6e^-

6e^- + 3Br²_(l) ↔ 6Br^-_(aq)

Step 3: From the balanced half reactions, we can conclude the number of moles of e^- for use later in the calculation of ∆G. Determine the E° values using the standard reduction potentials, using the E° cell table.

2Al_2(s) ↔ Al³⁺_(aq) +6e- -1.676V

3Br_2(l) + 6e^- ↔ 6Br^-_(aq) +1.065V

Step 4: Determine E°_cell = E°_cathode - E°_anode.

= 1.065 - (-1.676)

= 2.741 V

Step 5: Once E° cell has be calculated and the number of moles of electrons have been determined, we can use ∆G = -nFE°_cell

= (-6 mol e^-)(96485 C/mol e^-)(2.741 V)

= -1586kJ

This equation can be used to calculate E° cell given K or K given $E^o_{cell}$. If T=298 K, the RT is a constant then the following equation can be used: E°_cell= (0.025693V/n) ln K

Example 5: Using E° cell=(RT/nF) lnK

Given the $E^°_{cell}$ for the reaction

$$\ce{Cu(s) + 2H^{+}(aq) \rightleftharpoons Cu^{2+}(aq) +H2(g)} \nonumber$$

is -0.34V, find the equilibrium constant ($K$) for the reaction.

Solution

Step 1: Split into two half reaction

$$\ce{Cu(s) <=> Cu^{2+}(aq)} \nonumber$$

$$\ce{2H^{+}(aq) <=> H2(g)} \nonumber$$

Step 2: Balance the half reactions with charges to determine n

Cu_(s) ↔ Cu²⁺_(aq) + 2e^-

2H⁺_(aq) +2e^- ↔ H_2(g)

Therefore n=2

Step 3: From the example above, $E^°_{cell} = -0.34\,V$

$$\begin{align*} -0.34 &= \left(\dfrac{0.025693}{2} \right) \ln K \\[4pt] K &= \exp \left(\dfrac{-0.34 \times 2}{0.025693}\right) \\[4pt] K &= 3.19 \times 10^{-12} \end{align*}$$

Example 6: Spontaneity

Given the following reaction determine $∆G$, $K$, and $E^o_{cell}$ for the following reaction at standard conditions? Is this reaction spontaneous?

$$\ce{Mn^{2+}(aq) + K(s) <=> MnO2(s) + K(aq)} \nonumber$$

Solution

Step 1: Separate and balance the half reactions. Label which one is reduction and which one is oxidation. Find the corresponding $E^o$ values for the half reactions.

$$\ce{MnO2(s) + 4H^{+}(aq) + 2e^{-} <=> Mn^{2+}(aq) + 2H2O(l)} \nonumber$$

Reduction with $E_{SRP}$ of +1.23V

$$\ce{K^{+}(aq) + e^{-} <=> K(s)} \nonumber$$

Oxidation with $E_{SRP}$ of -2.92V

Step 2: Write net balanced reaction in acidic solution, and determine the E° cell.

$$\begin{align*} E^o_{cell} &= E^o_{SRP}(cathode) - E^{°}_{SRP} (anode) \\[4pt] &= +1.23\,V - (-2.92\,V) = 4.15\,V \end{align*}$$

Mn²⁺_(aq) + 2K⁺_(aq) + 2H₂O_(l) ↔ MnO_2(s) + 4H⁺_(aq) + K_(s) E° cell = 4.15V

Step 3: Find ∆G for the reaction.

Use ∆G = -nFE°_cell

= -2 mol e^- x 96485 C x 4.15 = -800.60kJ

Therefore, since $E^o_{cell}$ is positive and $∆G$ is negative, this reaction is spontaneous.

Exercise $\PageIndex{1}$

Find $E^o_{cell}$ for $\ce{2Br^{-}(aq) + I2(s) <=> Br2(s) + 2I^{-}(aq)}$

Answer

+0.530 V

Exercise $\PageIndex{2}$

Find $E^o$ for $\ce{Sn(s) <=> Sn^{2+}(aq) + 2e^{-}}$

Answer

+0.137 V

Exercise $\PageIndex{3}$

Find $E^o$ cell for $\ce{Zn(s) | Zn^{2+}(aq) || Cr^{3+}(aq), Cr^{2+}(aq)}$

Answer

+0.339 V

Exercise $\PageIndex{4}$

Find ∆G for the following combined half reactions:

$$\ce{F2(g) + 2e^{-} <=> 2F^{-}(aq)} \nonumber$$

$$\ce{Li^{+}(aq) + e^{-} <=> Li(s)} \nonumber$$

Answer

+1139.68 kJ

Exercise $\PageIndex{5}$

Find the equilibrium constant ($K$) for the following reaction:

$$\ce{Zn(s) + 2H^{+}(aq) <=> Zn^{2+}(aq) + H2(g)} \nonumber$$

Hint: Find $E^o_{cell}$ first!

Answer

6.4 x 10²⁵

Exercise $\PageIndex{6}$

Find $E^o_{cell}$ for the given reaction at standard conditions:

$$\ce{Cu^{+}(aq) + e^{-} <=> Cu(s)} \nonumber$$

$$\ce{I2(s) + 2e^{-} <=> 2I^{-}(aq)} \nonumber$$

Answer

+0.195 V

References

1. Brady, James E., Holum, John R. “Chemistry: The Study of Matter and Its Changes”, John Wiley & Sons Inc 1993
2. Brown, Theodore L., LeMay, H. Eugene Jr. “Chemistry: The Central Science” Third Edition, Prentice-Hall, Inc. Englewood Cliffs, N.J. 07632 1985
3. Brown, Theodore L., LeMay, H. Eugene Jr., Bursten, Bruce E. “Chemistry: The Central Science” Fifth Edition, Prentice-Hall, Inc. Englewood Cliffs, N.J. 07632 1991
4. Gesser, Hyman D. “ Descriptive Principles of Chemistry”, C.V. Mosby Company 1974
5. Harwood, William, Herring, Geoffrey, Madura, Jeffry, and Petrucci, Ralph, General Chemistry: Principles and Modern Applications, Ninth Edition, Upper Saddle River,New Jersey, Pearson Prentice Hall, 2007.