14.1: Bonding in Metals

The electron pair description of chemical bonds, which was the basis of the octet rule for p-block compounds, breaks down for metals. This is illustrated well by Na metal, the structure of which is shown at the left. Na has too few valence electrons to make electron pair bonds between each pair of atoms. We could think of the Na unit cell as having eight no-bond resonance structures in which only one Na-Na bond per cell contains a pair of electrons.

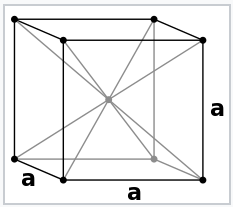
Sodium metal crystallizes in the body-centered cubic structure, in which each atom has eight nearest neighbors. Since the electronic configuration of Na is [Ar]3s^1, there are only two valence electrons per unit cell that are shared among eight Na-Na bonds. This means that the Na-Na bond order is 1/8 in Na metal.

A more realistic way to describe the bonding in metals is through band theory. The evolution of energy bands in solids from simple MO theory (Chapter 2) is illustrated at the right for a chain of six Na atoms, each of which has one 3s valence orbital and contributes one valence electron. In general, n atomic orbitals (in this case the six Na 3s orbitals) will generate n molecular orbitals with n-1 possible nodes. In Chapter 2, we showed that the energy versus internuclear distance graph for a two hydrogen atom system has a low energy level and a high energy level corresponding to the bonding and antibonding molecular orbitals, respectively. These two energy levels were well separated from each other, and the two electrons in H₂ energetically prefer the lower energy level. If more atoms are introduced to the system, there will be a number of additional levels between the lowest and highest energy levels.

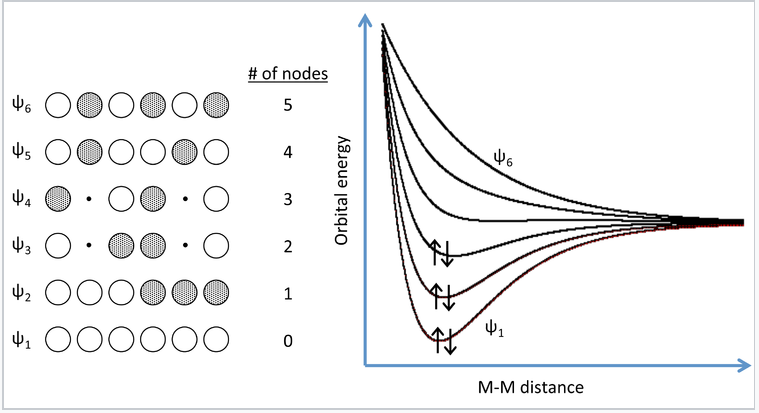
MO picture for a linear chain of six Na atoms. Three of the six MOs can accommodate all six valence electrons. Adding more atoms to the chain makes more molecular orbitals of intermediate energy, which eventually merge into a continuous band of orbitals. For Na, the 3s band is always half-filled because each MO can accommodate two electrons.

In band theory, the atom chain is extrapolated to a very large number - on the order of 10²² atoms in a crystal - so that the different combinations of bonding and anti-bonding orbitals create "bands" of possible energy states for the metal. In the language of physics, this approach of building the bands from discrete atomic orbitals is called the "tight-binding" approximation. The number of atoms is so large that the energies can be thought of as a continuum rather than a series of distinct levels. A metal will only partially fill this band, as there are fewer valence electrons than there are energy states to fill. In the case of Na metal, this results in a half-filled 3s band.

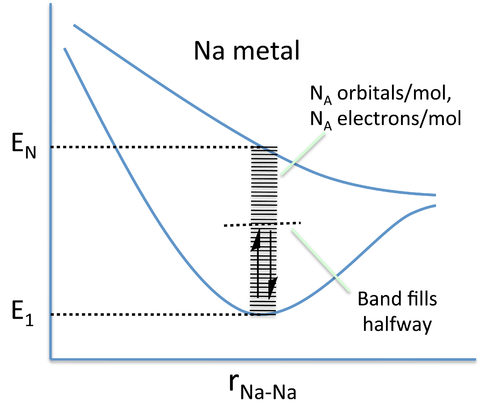
Nearly free electron model

In metals, the valence electrons are delocalized over many atoms. The total energy of each electron is given by the sum of its kinetic and potential energy:

E = KE + PE

E ≈ p²/2m + V

where p is the momentum of the electron (a vector quantity), m is its mass, and V is an average potential that the electron feels from the positive cores of the atoms. This potential holds the valence electrons in the crystal but, in the free electron model, is essentially uniform across the crystal.

Electron wavelength and wavenumber

What are the consequences of this model for band theory? For a hypothetical infinite chain (i.e., a 1D crystal) of Na atoms, the molecular orbitals at the bottom of the 3s band are fully bonding and the wavelength of electrons (2x the distance between nodes) in these orbitals is very long. At the top of the band, the highest orbital is fully antibonding and the wavelength is 2 times the distance between atoms (2a), since there is one node per atom. Remember that the wavelength of an electron (λ) is inversely proportional to its momentum p, according to the de Broglie relation λ = h/p.

For a (nearly) free electron, the kinetic energy can be expressed in terms of its wavelength, using KE = p²/2m and the de Broglie relation:

\[KE=\frac{p^{2}}{2m} = \frac{h^{2}}{2m\lambda ^ {2}}\]

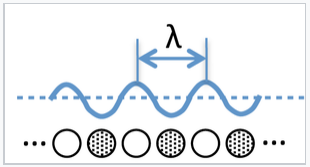
We can think of the wavelength of an electron in a molecular orbital as twice the distance between nodes. If there are N atoms in a linear chain, the wavelength of the nth orbital is given by λ = 2Na/n, where a is the distance between atoms.

At this point, it is convenient to define the wavenumber of the electron as k, which has units of inverse length and is inversely proportional to λ. k is also directly proportional to the momentum p. Like p, k is a vector quantity. In a 1D crystal, k can be either positive or negative, corresponding to an electron moving to the left or right along the chain.

\[k = \frac{2\pi}{\lambda} = \frac{2\pi p}{h} \: \: \textrm{where h is Planck's constant}\]

The most important property of k is that it is directly proportional to the number of nodes n in a molecular orbital within the band. For a 1D crystal of sodium atoms that contains N unit cells, each separated by a distance a, a molecular orbital with n nodes has a wavelength λ = 2Na/n and the wavenumber k = πn/Na. We can see from this definition that k = 0 at the bottom of the band (where λ is infinite) and k = π/a at the top of the band where the MO contains N nodes and λ = 2a.

Energies of orbitals in a metallic crystal

Electrons with long wavelengths do not "feel" the individual atoms in the lattice and so they behave as if they are nearly free (but confined to the crystal). Near the bottom of the band, the electron energy increases parabolically with the number of nodes (KE ∝ n²), since the momentum p is directly proportional to n. Because p is also directly proportional to k, we can write:

\[KE= \frac{p^{2}}{2m} = \frac{h^{2}k^{2}}{8\pi ^ {2}m}\]

This parabolic relationship is followed as long as the electron wavelength is long compared to the distance between atoms. Near the top of the band, the wavelength becomes shorter and the electrons start to feel the positively charged atomic cores. In particular, the electrons prefer to have the maxima in their wavefunctions line up with the atomic cores, which is the most electrostatically favorable situation. The electron-atom attraction lowers the energy and causes the E vs. k curve to deviate from the parabolic behavior of a "free" electron as shown in the figure below.

Density of States (DOS)

The density of states is defined as the number of orbitals per unit of energy within a band. Because of the parabolic relation between E and k, the density of states for a 1D metallic crystal is highest near the bottom and top of the energy band where the slope of the E vs. k curve is closest to zero. The shape of the DOS curve is different in crystals of higher dimensionality as shown in the figure in the left, because statistically there are more ways to make an orbital with N/2 nodes than there are with zero or N nodes. The situtation is analogous to the numbers you can make by rolling dice. With one die, the numbers 1-6 have equal probability. However, with two dice there is only one way to make a two (snake eyes) or a twelve (boxcars), but many ways to make a seven (a winner!).

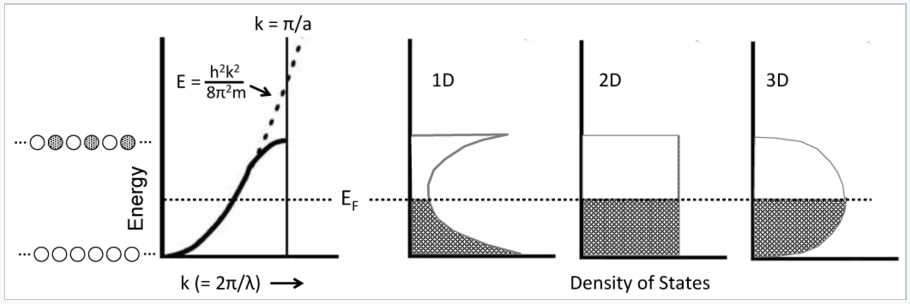
Electrons in metals follow a parabolic dispersion curve, where the energy increases with the square of the wavenumber, k. Near the top of the band, the dispersion curve deviates from the parabolic dotted line. Because there is one MO for each value of k, the number of orbitals per unit energy (the density of states, DOS) is highest at the bottom and top of the band for a 1D chain of atoms. The density of states is constant with energy for a 2D crystal, and has a maximum in the middle of the band for a 3D crystal. At low temperature, all the MOs below the Fermi level EF are occupied, and all the MOs above it are empty.

While most of the time we will talk about 3D crystals that have their maximum DOS near the middle of the energy band, there are examples of quasi-1D systems, such as carbon nanotubes. Metallic carbon nanotubes have strong optical absorption bands that correspond to transitions between the two regions of high DOS (the van Hove singularities) near the bottom and top of the bands.

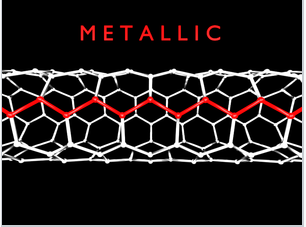
Single-walled carbon nanotubes with "armchair" chirality are metallic and have characteristic sharp absorption bands in the infrared. Prof. Millie Dresselhaus (below) did foundational research on the electronic properties of carbon nanotubes and other low-dimensional conductors.

Metals, semiconductors, and insulators

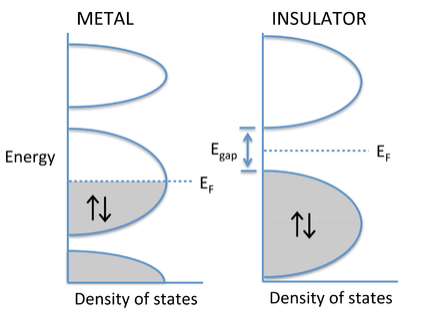
The degree to which bands fill determines whether a crystalline solid is a metal, semiconductor, or insulator. If the highest occupied molecular orbitals lie within a band - i.e., if the Fermi level E_F cuts through a band of orbitals - then the electrons are free to change their speed and direction in an electric field and the solid is metallic. However, if the solid contains just enough electrons to completely fill a band, and the next highest set of molecular orbitals is empty, then it is a semiconductor or insulator. In this case, there is an energy gap between the filled and empty bands, which are called the valence and conduction bands, respectively. Although the distinction is somewhat arbitrary, materials with a large gap (> 3 eV) are called insulators, and those with smaller gaps are called semiconductors. We will learn more about the properties of semiconductors in Chapter 10.

Why don't insulators conduct electricity? The energy vs. DOS diagram below shows what happens when an electric field is applied to a metal or an insulator. In this case we have changed the diagram to show explicitly the energies of electrons moving left and right. These energies are the same in the absence of an electric field. Once we apply a field (e.g., by putting a voltage across a metal wire), the electrons moving in the direction of the field have lower energy than those moving in the opposite direction. In the case of the metal, the populations of electrons moving with and against the electric field are different, and there is a net flow of current. Note that this can happen only when the Fermi level cuts through a partially filled band. With a semiconductor or insulator, the valence band is filled and the conduction band is empty. Applying an electric field changes the energies of electrons traveling with and against the field, but because the band is filled, the same number are going in both directions and there is no net current flow.

E vs. DOS diagrams comparing the behavior of metals and insulators in an applied electric field.

Note that in this picture, all the molecular orbitals extend over the entire crystal. The valence electrons are delocalized, even in the case of a semiconductor or insulator. However, there can be no net movement of electrons unless the band is partially filled.